例谈用导数解决几何中的优化问题
■邓礼伍
作为研究两个变量之间变化规律的有力工具,导数在解决几何背景下的优化问题方面有着广泛应用。利用导数解决这类问题,首先,作图并分析图形中的几何关系;其次,构建函数模型并表述出变量间具体的函数关系式;最后,利用导数性质求解相关问题。本文将结合实例介绍利用导数解决几何中的优化问题。
一、函数的单调性、最值与导数之间的关系
在区间(a,b)上,若函数y=f(x)满足f'(x)>0,则函数y=f(x)在(a,b)上是增函数;若函数y=f(x)满足f'(x)<0,则函数y=f(x)在(a,b)上是减函数。
若函数y=f(x)在(a,b]上是增函数,在(b,c)上是减函数,则函数y=f(x)在(a,c)上有最大值为f(b)。若函数y=f(x)在(a,b]上是减函数,在(b,c)上是增函数,则函数y=f(x)在(a,c)上有最小值为f(b)。
若函数y=f(x)在[a,b]上是增函数,则函数y=f(x)在[a,b]上有最小值为f(a),最大值为f(b);若函数y=f(x)在[a,b]上是减函数,则函数y=f(x)在[a,b]上有最大值为f(a),最小值为f(b)。
二、求解函数最值的一般步骤
众所周知,用导数求解函数最值可以起到化繁为简的作用,大大节省时间。熟练运用导数求解函数问题是一种非常重要的解题技能。那么,导数求解函数最值又有哪些步骤呢?
第一步:确定定义域并求导函数y=f'(x)。
第二步:求解方程f'(x)=0。
第三步:求出函数y=f(x)在闭区间端点和使得f'(x)=0的点的函数值并比较大小,这些函数值中最大的为最大值,最小的则是最小值;倘若求函数在开(或半开半闭)区间上的最值,则需先讨论函数的单调性,再依据单调性求最值。
三、用导数解决几何中的优化问题
例1一个近似球形的玉石原料,半径为R,现要加工成内接正四棱锥形状的成品,则正四棱锥的高为多少时,所得成品的体积最大?
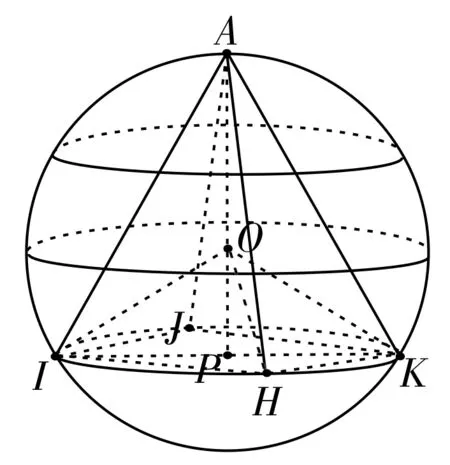
图1
解:如图1所示,易知当A,P两点分别位于O点两侧时,四棱锥的体积才可能达到最大。设球心到底面的距离OP=x(0≤x<R),则三棱锥的高AP=R+x。在Rt△OPH中,运用勾股定理可得。于是,可求出底面正方形HIJK的面积为2(R2-x2)。
设四棱锥A-HIJK的体积为V(x),那么该四棱锥的体积函数为,求导可得V'(x)=-2x2-,令V'(x)=0,解得或x=-R(舍去)。当时,V'(x)>0,V(x)为增函数;当时,V'(x)<0,V(x)为减函数。故时,V(x)最大,即正四棱锥的高时,所得正四棱锥的体积最大。
评注:本题虽涉及几何知识,但本质上仍然是一个典型的函数优化问题。主要考查作图、几何图形的体积和面积公式、构建函数模型、表述函数关系式,以及运用导数处理函数最值等多个知识点和技能。类似地,也可以求解球内接正四棱柱的最大体积问题,详见例2。
例2(2006年江苏)请您设计一个帐篷,它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图2所示)。试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大。
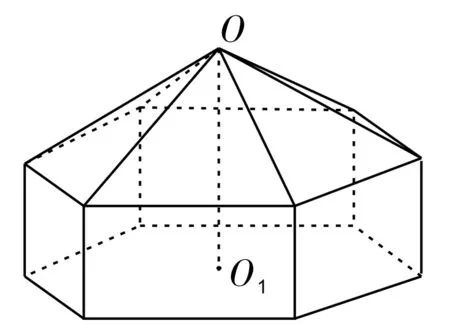
图2
解:设OO1为xm(1<x<4),则由题意可得底面正六边形的半径为。由正六边形的性质可知,底面正六边形的边长为。因此,底面正六边形的面积(单位:m2)为。显然,帐篷的体积(单位:m3)等于上部的正六棱锥与下部的正六棱柱的体积和,因此V(x)=,求导可得令V'(x)=0,解得x=2或x=-2(舍去)。当1<x<2时,V'(x)>0,V(x)为增函数;当2<x<4时,V'(x)<0,V(x)为减函数。所以当x=2时,V(x)最大。故当帐篷的高OO1为2m时,帐篷的体积最大。
评注:找准几何图形中线段之间的数量关系是解决几何优化问题的前提。在此前提下,再利用导数即可快速解决问题。
四、结束语
结合文中的实例及平时遇到的类似问题,我们不难发现看似复杂的几何问题,实际上运用导数求解的过程却并不复杂。利用导数可以有效降低难度,简化运算,因此灵活运用导数这一有力工具处理最值、极值问题是相当高效的。

