轨道炮发射过程中轨道的受力与变形问题研究*

崔孟阳,王学智,丁日显,童思远,陈青荣

(1 空军工程大学研究生院, 西安 710051； 2 空军工程大学防空反导学院, 西安 710051)

0 引言

电磁轨道炮利用流经轨道、电枢的大电流产生的强磁场,使电枢在洛伦兹力的作用下加速运动到轨道炮出口,并抛射出去,是一种新概念动能武器。由于电枢运动速度较快,为保证电枢和轨道始终具有较好的接触,需要对轨道施加适当的预紧力。在发射过程中,电枢受到电磁力并且发生变形,会对接触的轨道面产生挤压。两侧的轨道由于流过相反方向的强电流,也会产生较大的排斥力。因此,保证轨道处于较为稳定的工作状态,并且具有较长的使用寿命,是电磁轨道发射技术的重要研究方向[1]。

对于在发射过程中轨道的变形问题,许多学者进行了相关研究。文献[2]中将电磁发射装置的轨道简化为移动载荷作用下弹性简支梁来分析其受力与变形；文献[3]中将方口径电磁发射装置的导轨及壁板简化为双层弹性基础梁来分析导轨及壁板的动力响应；文献[4]中将简化为弹性地基梁的导轨控制方程进行Fourier变换,推导出发射过程中导轨的动态响应方程,分析了导轨几何参数、通入电流的强度及外包层的弹性特征等量对导轨动态响应的影响。

文中利用Maxwell电磁分析软件建立了电磁轨道炮的仿真模型,分析通入电流之后轨道炮的电磁场分布情况,得到体积力密度分布情况，并将数据导入Ansys Workbench的Static Structural模块,进行仿真得到电枢和轨道的变形情况和等效应力分布情况。

1 轨道的受力分析模型

电磁轨道炮的结构模型如图1所示。电枢在两轨道之间产生的强磁场作用下,受到较强的洛伦兹力作用使其沿着轨道移动。电枢在沿着轨道运动的过程中,会对轨道造成挤压。同时轨道还会受到相邻轨道的排斥力,以及外包层对轨道产生的预紧力。轨道的受力情况如图2所示。

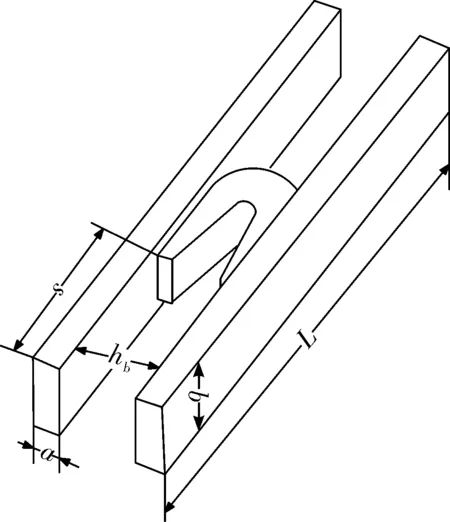
图1 轨道炮结构模型图

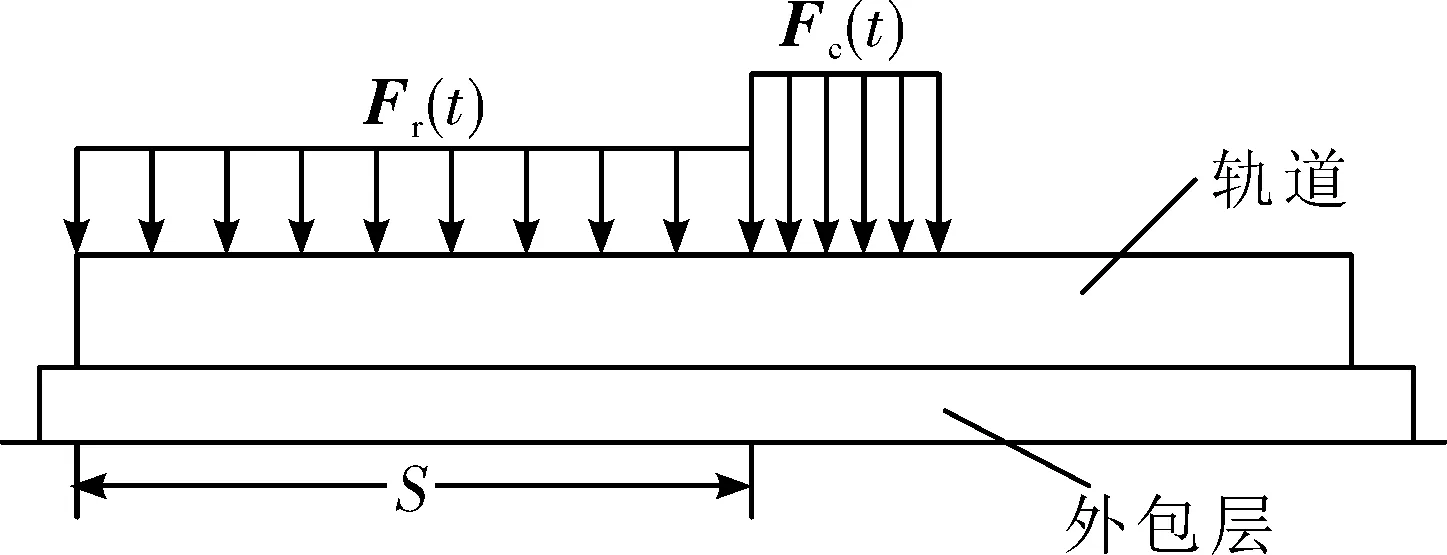
图2 轨道的受力简图

在轨道的受力分析中,假设导轨的两端没有约束,外包层为轨道提供弹性支撑。轨道的动力学控制方程[7]为：

(1)

式中：w(x,t)为轨道的横向变形;E为轨道材料的杨氏模量;Iy是轨道横截面惯性矩;k为外包层支撑的弹性系数;ρ是轨道的材料密度;A为轨道的横截面积;q(x,t)为轨道受到的载荷。

对式(1)进行关于x、t的傅里叶变换,得[7]:

(2)

其中,α、β是傅里叶变换中的积分变量。得：

(3)

对式(3)进行傅里叶逆变换得：

(4)

即为在发射过程中轨道的横向变形量。

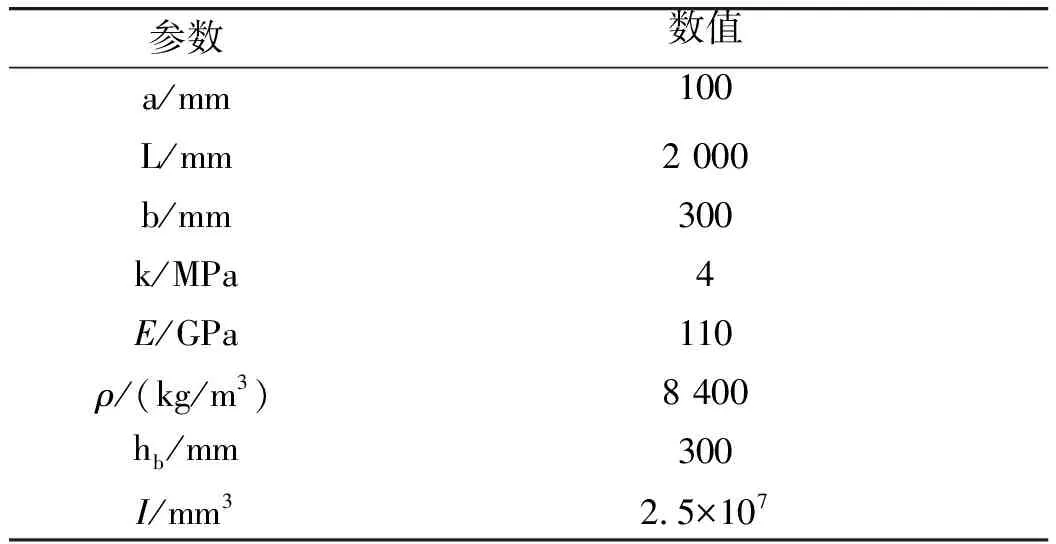
表1 数值计算参数

2 轨道相关受力分析

轨道所受到的应力主要有：电枢受电磁力发生变形对轨道造成挤压应力,相邻轨道之间的排斥力以及电磁轨道炮外包层对轨道的预紧力。电枢与轨道的接触应力是相互的,分析计算电枢在运动时所受电磁力在垂直于枢轨接触面方向上的分力,就可以得到电枢对轨道的挤压应力。

2.1 轨道间的相互作用力

因为轨道炮在发射的过程中,存在明显的电流趋肤效应。因此作出假设：1)电流在轨道内表面存在一定的趋肤深度；2)电流集中在趋肤深度的中心线位置。

实际应用中电枢尾翼的电流段相对轨道上的电流段较短,因此忽略其对轨道的排斥作用。

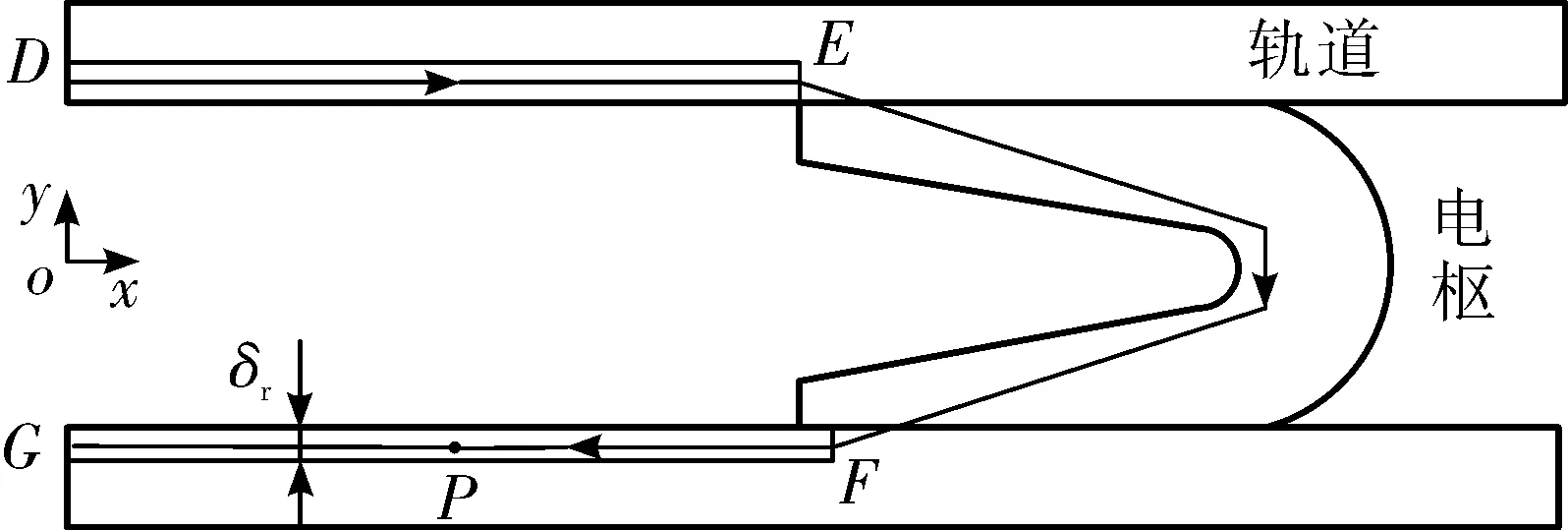
图3 轨道炮的原理图

在t时刻,DE段的电流在GF段的内点P(x1,-(hb+δr)/2)处生成的磁场强度[5]可通过以下式子计算：

(5)

式中：δr为轨道的电流趋肤深度；hb为两侧导轨的间距；x1为点P距轨道尾部端面的距离；s为电枢的位移。在轨道通入电流之后,点P处单位长度的轨道受到另一轨道的电磁排斥力为:

Fr=BDEI

(6)

2.2 电枢与轨道接触应力

电流经轨道流向电枢,并形成闭合回路。根据通入电流的大小,可以计算出发射场内任一点的磁感应强度。对电枢所在位置的磁场强度进行计算,并根据流经电枢的电流大小计算出电枢受到的洛伦兹力。

将载流长方体轨道看成由许多载流直导线组成,当轨道和电枢中通入电流时,左侧轨道电流源点坐标为m(x′,y′,z′),取电枢上中心点坐标为q(x(t),0,0),则m点的电流元Idxi在q点产生的磁感应强度[7]为:

(7)

对式(7)进行积分,可得左侧轨道在q点产生的磁场强度。

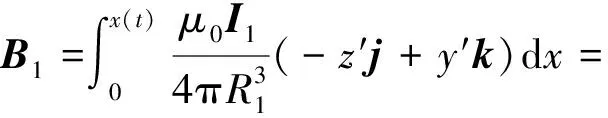
(-z′j+y′k)dx

(8)

同理可得右侧轨道在q点产生的磁场强度为：

(9)

以上式中i、j、k分别为X、Y、Z轴方向上的单位向量；μ0为真空磁导率。

根据磁场叠加原理,可得轨道电流在q点产生的磁场强度为:

B=B1+B2

(10)

电枢在磁场中的受力为：

(11)

根据牛顿第三运动定律,电枢与轨道的挤压应力是相互的。电枢对轨道的挤压应力[4]为：

Fc(t)=βF1

(12)

式中：β为电枢沿垂直于轨道接触面方向上的电磁力分力转化为挤压应力的转换系数。

2.3 轨道所受应力计算

轨道所受应力的计算公式[10]为：

F(t)=Fc(t)+Fr(t)+F0

(13)

式中：F0是轨道炮外包层对轨道外部的机械预紧力。

3 仿真与分析

在Ansys Maxwell电磁分析软件中建立电磁轨道炮的仿真模型,轨道材料为铜合金,电枢材料为铝合金。轨道炮的其他参数如表2所示。

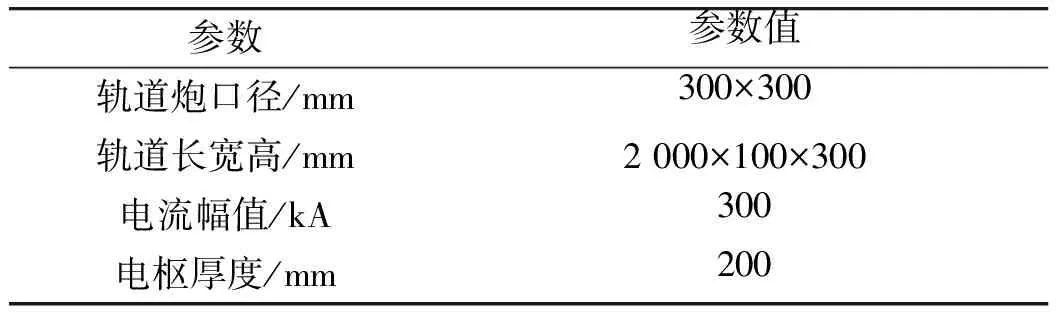
表2 轨道炮基本参数

3.1 建模仿真

在Maxwell中进行电磁仿真,可以得到轨道和电枢上的电流分布情况、膛内的磁场分布情况以及轨道炮各部位的体积力密度。其中体积力密度的矢量图如图4所示,可以看到电枢和轨道不同部位的受力情况：两侧轨道均受到向外的排斥力；电枢尾翼受到的电磁力也朝向与其接触的轨道一侧,该电磁力会使电枢发生位移或变形挤压轨道。

将在Maxwell建立好的电磁轨道炮模型和分析结果导入Ansys Workbench,建立电磁-应力耦合仿真分析模型,在Static Structural模块进行应力变形有限元分析。在只对轨道的两端作固定约束的情况下,模拟轨道和电枢的变形情况。

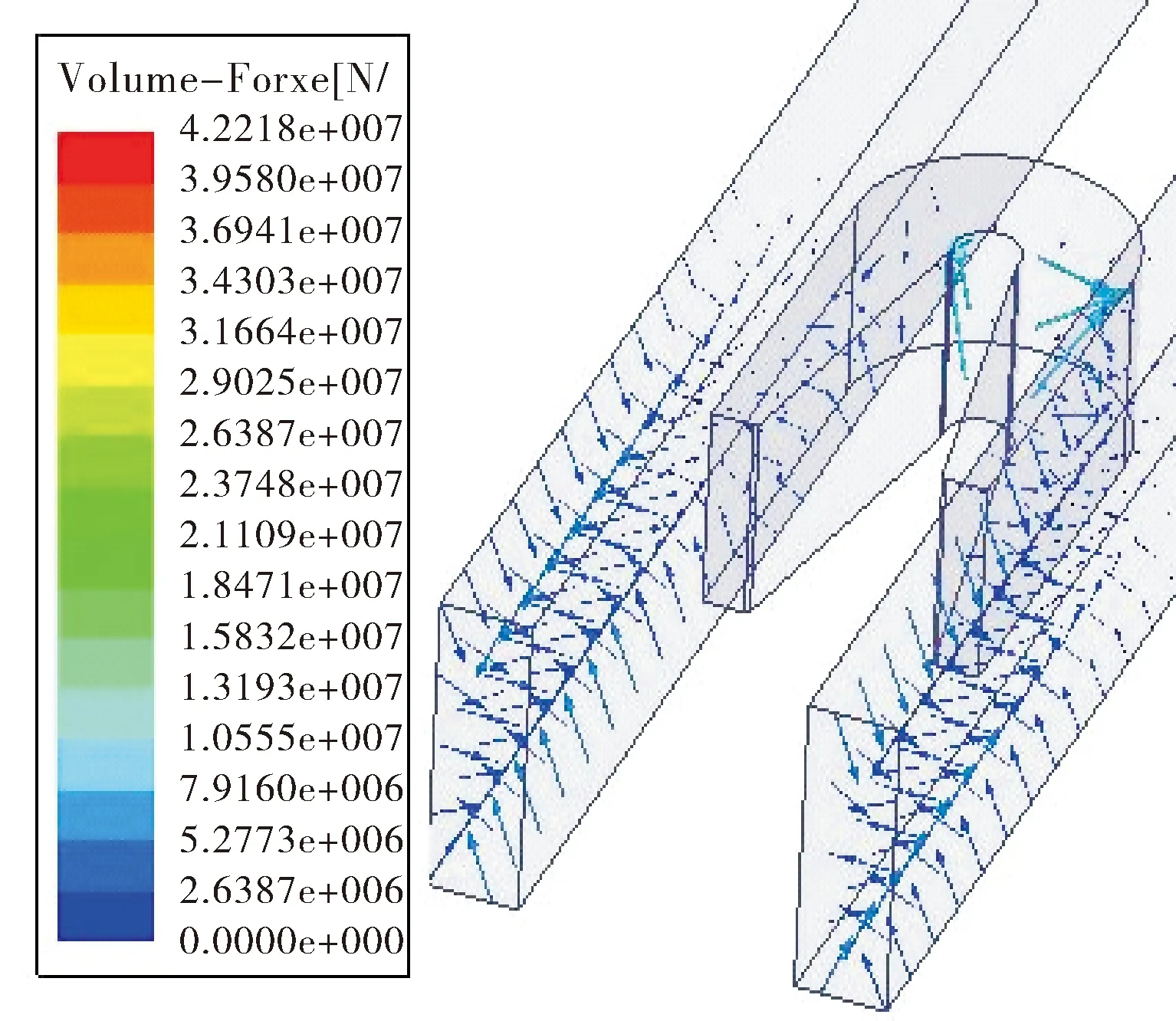
图4 体积力密度分布图

当电枢运动距离分别为800 mm和1 700 mm时,电枢和轨道的等效应力云图和变形情况如图5所示。随着电枢的位移,膛内的磁场会发生变化,轨道之间的电磁排斥力逐渐增大；轨道的外部两侧应力较大,中间部位应力较小；电枢的尾翼因为受到强电磁力发生形变对轨道挤压,是枢轨接触压力增大的重要原因。

3.2 枢轨接触面的应力分析

在进行电磁-应力耦合仿真时,对两个轨道的外侧施加固定约束,通过Sweep方法对轨道和电枢进行网格划分。当电枢位移距离为1 100 mm时,电枢与轨道接触面的应力分布情况如图6和图7所示。由图6可得：电枢表面的应力分布由末端到肩部是逐渐增大的,电枢的肩部存在应力集中,因此在实际应用中也需要对电枢的肩部进行特殊的处理。

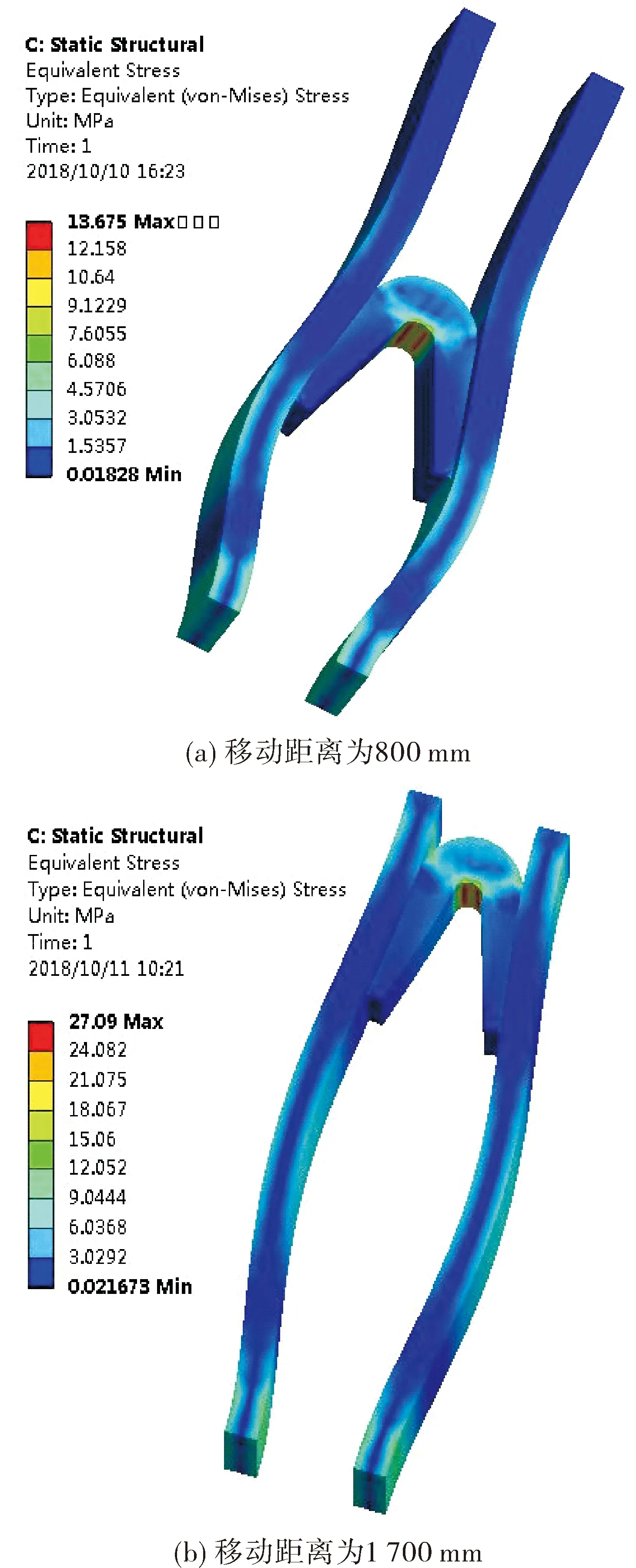
图5 轨道炮的等效应力与变形图

轨道上的应力分布如图7所示,与电枢接触部位的应力分布情况基本和电枢相同：较大应力集中在与电枢肩部接触的部位；轨道与电枢尾部的接触面外侧应力要大于中间部位的；电枢运动过的轨道部位应力值较小,为轨道之间的排斥力；未通入电流的轨道段几乎无应力分布。

当施加的激励电流幅值分别为150 kA和300 kA时,轨道内侧表面中心线位置的应力与位置关系如图8所示。以通入300 kA电流为例,电枢运动过的轨道部位排斥力约为1.49 MPa,轨道上所受的最大应力约为4.46 MPa。电枢未滑过的轨道部位压力逐渐减小,这与前面的理论分析保持一致。随着电枢位置的移动,枢轨接触面上的最大应力分布如图9所示,电枢运动距离的增加使最大接触应力有所增大,但增幅不大；激励电流幅值为300 kA时的最大接触应力约为150 kA的4倍。

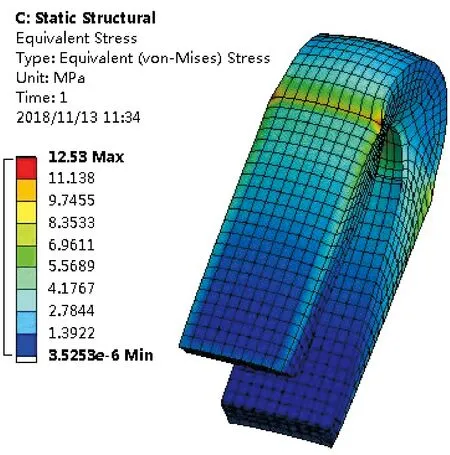
图6 电枢的等效应力图

图8 轨道上的应力与位置的关系

4 结论

利用Ansys Workbench有限元仿真软件建立电磁-应力多物理场耦合模型,通过Maxwell仿真得到体积力密度、电流和磁场分布并导入到Static Structural模块进行仿真分析,得到发射过程中轨道受到的应力分布与变形情况。

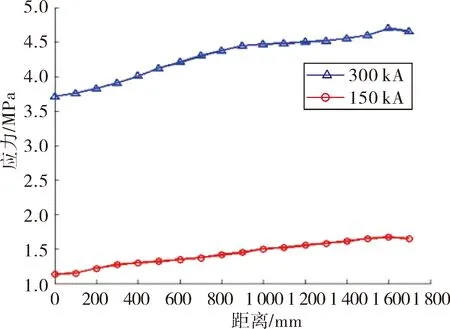
图9 电枢在不同位置接触面上的最大应力

1)电枢滑过区域的轨道,因为电枢的挤压和轨道之间的排斥力,变形挠度较大；未滑过区域的轨道变形相对较小。

2)在发射过程中,电枢的尾翼受到较强电磁力会往外侧张开,电枢和轨道的材料在满足耐磨损的条件下,可以保证电枢和轨道有良好的接触。

3)电枢对轨道的挤压、轨道之间的排斥力都会导致轨道变形。

为了保证发射精度,需要控制轨道炮的口径变化。增强轨道的抗弯刚度,减小轨道的挠度幅值可以改善轨道炮工作的稳定性,有利于实现电磁轨道炮的安全连续发射。