基于改进的一次二阶矩法的末敏子弹旋开机构优化设计*
刘慧玲,徐建军,彭志凌
(中北大学机电工程学院, 太原 030051)
0 引言
末敏弹是灵巧弹药的一种。末敏子弹主要由降落伞/翼系统、弹上计算机、敏感器、爆炸成形弹丸(explosively formed penetrator,EFP) 战斗部及安全起爆装置等组成[1]。末敏子弹由携带器带到目标区上空,利用抛撒装置将末敏子弹从携带器中按一定图形分离抛撒出来[2]。末敏子弹减速减旋并分开一定距离,抛掉减速伞,释放旋转伞,进入稳态扫描状态,末敏子弹自主的对目标进行搜索、探测、识别[1]。毫米波敏感器就是利用不同物体在毫米波段上的电磁波辐射特性的差别进行探测识别[3]。
旋开机构用于释放毫米波敏感器,实现末敏子弹药工作状态的转换。在旋开机构解除锁定后,发条作为贮能元件带动旋开机构座绕轴转动,螺母在旋转的同时带动旋开机构座沿轴向运动。旋转至180°位置时,旋开机构座与装配底座端面安全贴合,两个面之间的间隙消除。在其旋开的过程中,同时完成解除安全起爆装置机械保险、释放毫米波敏感器并最终锁定到位等一系列动作。从旋开机构旋开过程可以看出,影响旋开机构可靠性的主要零件是发条,对旋开机构的优化设计主要是对发条的设计参数进行优化。
1 旋开机构可靠度模型
1.1 基于应力-强度干涉理论的可靠性模型
应力-强度干涉理论[4]的可靠度计算方法将影响机械产品失效的因素概括为应力和强度两类。假设零件的广义强度分布和广义应力分布是相互独立的,则在概率统计中,应力和强度的随机概率关系满足p(S|s)=p(S)。
设应力X的概率密度函数为f(x),强度Y的概率密度函数为g(y)。通常零件的强度高于其工作应力,但由于应力和强度的离散性,使应力和强度的概率密度函数曲线在一定时间内可能相交,见图1。图1中相交的阴影部分称为“干涉区”,可能产生失效。通常把这种干涉称为应力-强度干涉模型[5]。可靠度R和失效概率Pf分别为:
R=P(Y>X)=P(Y-X>0)
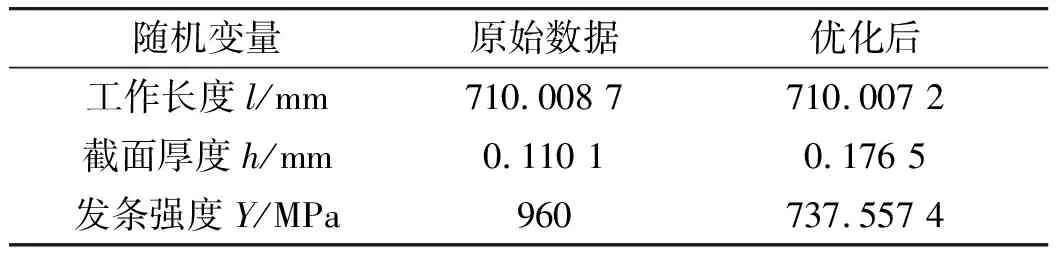
Pf=P(Y (1) 且有R+Pf=1。 图1 应力-强度干涉模型 利用改进的一次二阶矩法求解可靠度,设应力X和强度Y是相互独立的两个随机变量,令Z=Y-X,故Z的联合概率密度函数为: f(z)=f(x)g(y) (2) 根据可靠度的定义,强度Y大于应力X的概率为: (3) 末敏子弹在稳态扫描下降的过程中,会在适当的位置通过旋开机构使末敏子弹旋开错位,这时末敏子弹旋开成上下两个回转体,上回转体上的敏感器露出,通过敏感器的扫描、探测,在发现识别到目标以后,根据距离地面的高度、转速、识别算法及其他因素,计算最佳瞄准点,并依此选择起爆时机起爆战斗部。 图2 旋开机构安装示意图 图3 末敏子弹战斗状态 旋开机构的一系列动作都是由其内部的发条产生的,通过发条的力矩作用使末敏子弹旋开成上下两部分。发条是平面螺旋线型的一种非接触型平面涡卷弹簧。装配时发条一端固定,另一端作用扭矩,材料受弯曲力矩,产生弯曲弹性变形,其应力为: (4) 式中:T为发条扭矩;E为材料弹性模量;l为发条的有效工作长度;h为发条截面厚度;n为工作转数,n=4.5;K1为系数,外端固定时K1=1,外端回转时K1=1.25;K2为系数,外端固定时K2=1,外端回转时K2=2。 依据应力-强度干涉模型,用多元函数 (5) 表示,式(5)是发条的功能失效极限状态函数。 图4 旋开错位子弹体结构简图 均值一次可靠度方法在均值点处将功能函数取泰勒技术线性展开项,对于非线性功能函数或者非正态输入随机变量的结构可靠性分析问题,该方法的精确度有限[6]。 改进的一次二阶矩法的思想是将非线性功能函数做线性化处理,线性功能函数的线性优化点取在失效边界上,且选在了与最大失效概率对应的设计验算点p(见图5)[7]。 设结构的极限状态方程为: g=g(x1,...,xn)=0 (6) (7) 由于设计点x*落在极限方程g=g(x1,x2,...,xn)=0上,即有: (8) 在随机变量X空间,方程g(x)=0为过点x*处的极限状态面的切平面。利用相互独立的正态分布随机变量线性组合的性质,g(x)的均值和标准差分别为: (9) (10) (11) 对x进行标准正态变换,将式(7)用x的标准变化量y=(x-μxi)/σxi改写,并用式(10)作为法化因子遍除,整理后得: (12) 结合式(11)和式(12),式(12)又可写成: (13) 定义变量xi的灵敏度系数如下[8]: (i=1,2,3,…,n) (14) 式(14)可改写成: (15) 设计验算点p在标准化正态变量Y空间的坐标为: (16) 在原始X空间中的坐标为: (17) 图5 可靠度指标β的几何解释 在结构可靠性分析中,经常采用迭代求解可靠性指标β。假设功能函数为z=g(x1,x2,…,xn),求解过程如下: 2)假定x*的初始值,一般可设x*=μx; 3)运用式(14)计算灵敏度系数αi; 4)运用式(11)计算可靠度指标β; 失效概率按Pf=Φ(-β)计算。 由于非接触型平面涡卷弹簧的设计,一般先给出承受的转矩T和相应的角变形Ψ,再根据工作条件选出较为合适的材料,进行有关参数的计算,所以,将发条的主要优化参数选定为有效工作长度和截面厚度,它们可以看成独立且服从正态分布的随机变量。将式(5)记为Z=G(l,h,Y),则旋开机构的功能函数为: (18) 基于改进的一次二阶矩法,文中采用Matlab编制了计算程序,对末敏弹旋开机构进行了优化设计。发条所用材料的参数如表1。表2同时列出了原始数据和优化后各个参数的值。 表1 材料0Cr17Ni7Al参数 表2 基本随机变量统计特征 可靠度指标为β=23.889 9,失效概率Pf=1.949 29e-126。 将改进的一次二阶矩法与应力-强度干涉可靠度理论相结合,采用迭代方法,借助Matlab辅助计算,对旋开机构进行了优化设计。计算结果表明: 1)发条的截面厚度增加,工作长度几乎不变,对材料的强度的要求降低,整体的可靠度提高了。 2)改进的一次二阶矩法简单,易于实现,是旋开机构优化设计中较为理想的方法。 3)由于泰勒展开式仅取了线性项,所以它不能反映功能函数的非线性项对失效概率的影响。 4)具有多个设计点的问题,改进的一次二阶矩法有可能陷入局部最优,甚至不收敛。 5)可靠度指标越大,失效概率越小。
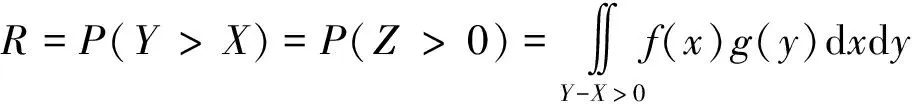
1.2 发条的可靠度模型



2 改进的一次二阶矩法




3 旋开机构结构优化设计
3.1 旋开机构的功能函数
3.2 旋开机构优化设计

4 结论

