带落角约束与过载约束的寻初比例导引法*
王煜东,许承东,郑学恩,孙光辉,简益梅
(北京理工大学宇航学院, 北京 100081)
0 引言
随着现代战争的发展,对导弹末端精确打击的要求越来越高。落角是导弹命中目标时速度矢量与水平面之间的夹角,落角越大,对目标的击顶效果越好,对落角提出更高的要求,能够使导弹末制导段的参数更加合理。国内外大多采用带落角约束的制导律来对落角加以限制,该方法主要分三类[1]:一是采用最优制导律的方法,如冯艳清[2]等人设计了带落角约束的三维导引律,可以对静止目标及低速目标以一定攻击角度进行攻击;张友安[3]等人结合落角、目标攻角及脱靶量设计了一种二次型最优制导律,能够满足在高精度的前提下以一定落角进行攻击。二是采用滑模制导律,Harl N[4]等人采用视线角整形技术推导出具有攻击时间与攻击角度约束的制导律,但是制导律形式十分复杂,制导指令需要大量迭代,只能离线完成;杨峰[5]等人提出了带落角约束的模糊变结构导引律,满足了制导精度与落角要求。三是采用改进比例导引法,Lee C H[6]等人在传统的比例导引法上加入落角约束,提出了带落角约束的偏置比例导引,但是该方法仅对固定目标有较好的效果,且还需要对剩余飞行时间进行估计,实用性受限。高峰[7]等人设计了一种三维联合偏置比例导引律,采用时变比例系数可对高速目标与低速目标分别拦截,是一种普适的制导律,但是在拦截初始段的需用过载要求比较大,并且还需要精确的估计剩余时间才能满足落角精度。比例导引法理论成熟,成果丰富,工程实现简单,因此文中采用比例导引法,在理论上推导落角的数学表达式,建立落角预测模型,根据模型结果选取恰当的比例系数,即可实现对预计目标以一定的落角进行打击,只需在导弹平飞段选择合适的攻击参数与导弹比例系数即可。
为简化分析,文中以图像制导导弹[8]为例,导弹最大可用过载为5,攻击目标为敌方坦克,命中目标时落角大于30°时即可达到理想效果。
1 寻初比例导引法
比例导引法是指导弹在攻击目标的导引过程中,导弹速度矢量旋转的角速度与目标线旋转角速度成比例。导弹在飞行过程中过载时刻在变化,传统的比例导引法无法保证命中时的落角,因此提出一种改进比例导引法,该方法通过寻找满足过载约束与落角约束的初始值,其中落角会随着初始目标线角q0增大而增大,过载会随着转比距离r0增大而减小,因此需要找到合适的q0及r0,使导弹命中目标时既满足过载约束,又能符合落角要求。
1.1 建立导弹相对运动方程
按比例导引时,导弹与目标之间的相对运动方程组为:
(1)
当导弹在铅垂面内从某一高度平飞到开始启动比例导引法进行末制导,导弹与目标相对运动关系如图1所示。

图1 导弹与目标相对运动关系
图中M0,M1,Mk分别是导弹由平飞段转到比例导引的初始位置,中间某一时刻位置,及命中目标时的位置;T为目标位置;初始距离为r0;选取Ax轴作为基准线,初始目标线角为q0,命中目标时目标线角为qk,导弹速度矢量及目标速度矢量与目标线之间的夹角为前置角,分别记作η,ηT;导弹速度矢量与目标速度矢量与基准线之间的夹角为导弹弹道角及目标航向角,记σ,σT。
1.2 落角的几何关系
落角即导弹速度矢量与水平线之间的夹角,由图1可知,落角近似等于命中目标时目标线角qk,由于qk未知,但是由几何关系可得:
qk=q0+(qk-q0)
(2)
将qk-q0记作目标线偏转角△q,得到落角公式:
qk=q0+Δq
(3)
由于初始q0为已知量,求得目标线偏转角Δq的范围,即可得出落角qk的范围。
1.3 Δq的解析表达
将式(1)中的第二个方程单独分析:
(4)
考虑到命中目标时距离为0,所以当rk=0时,式(4)化简为:
Vsinη=VTsinηT
(5)
将几何关系ηT=qk-σTk代入上式得到:
Vsinη=VTsin(qk-σTk)
(6)
由比例导引法定义可得:
η-η0=(1-K)(qk-q0)
(7)
联立式(6)与式(7),消去导弹速度前置角η,并将导弹速度与目标速度的速度比p引入该方程可得:
(8)
将式(8)右端qk-q0记作△q得到目标线偏转角的解析表达式为:
(9)
由式(9)可以看出,目标线偏转角与转比距离r0无关。
为简化分析,飞行速度保持恒定V=240 m/s,导弹射程为1~10 km,最大法向过载为n=5,导引头最大探测距离为3 km,导引头瞬时视场为4°×3°[9]。将数值进行仿真,画出弹道曲线如图2所示。
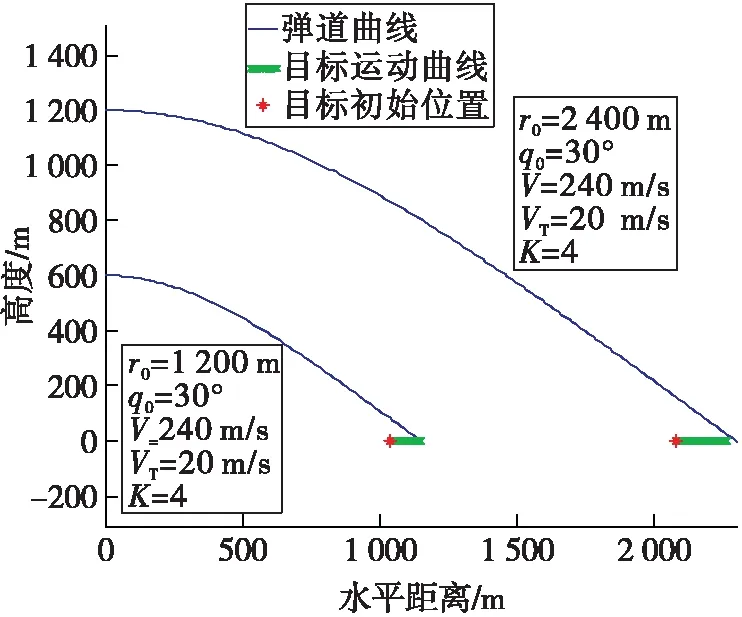
图2 不同转比距离的弹道曲线对比
观察到仅改变初始距离r0,q0为30°保持不变,两次计算出的落角均是38.99°,验证落角与r0无关。
1.4 落角预测模型
观察到式(9)中,式右端包含3个参数K、p、η0,及一个未知量qk,无法精确求得目标线偏转角的大小,但是由于sinqk在实际情况中有取值范围,即:
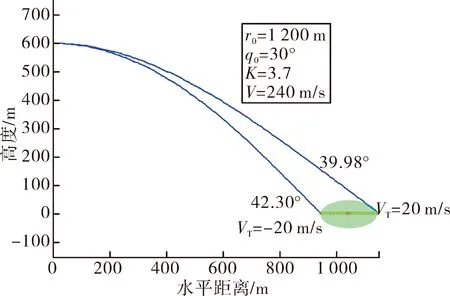
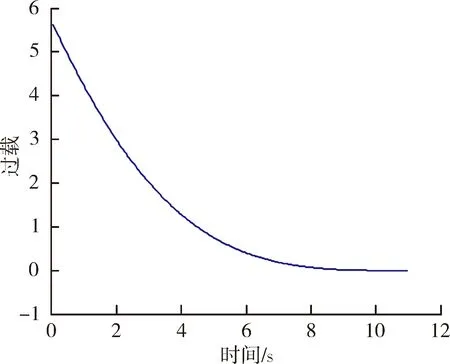
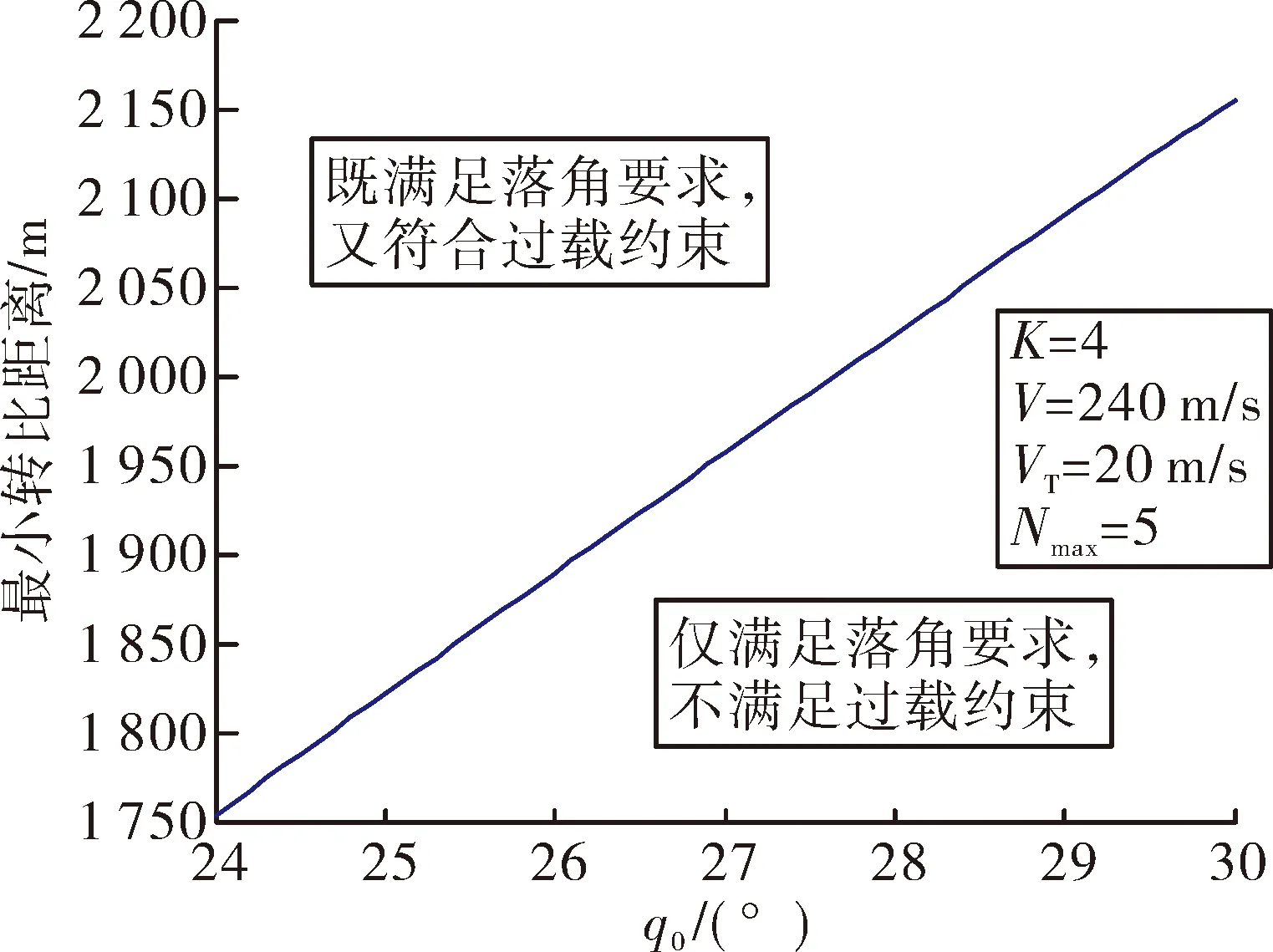
sinq0 (10) 将式(10)代入式(9)中,能得到Δq的取值范围为: Δqmin<Δq<Δqmax (11) 这两个端点数值均可以根据已知数据求出,当导弹从平飞转到比例导引的时候,平飞段的速度前置角η0正好等于开始转比的初始目标线角q0,所以Δq仅与比例系数K、速度比p、初始目标线角q0有关,可以看成这3个参数的函数: Δq=f(K,p,q0) (12) 首先确定速度比p,考虑到坦克机动的影响,设坦克分别以20 m/s的速度和-20 m/s的速度匀速前进,画出这两种弹道曲线如图3所示。 图3 不同速度比的弹道曲线对比 图3中红点是坦克初始位置,绿线是坦克前后两种运动轨迹,绿圈是以坦克初始位置为圆心,以坦克最大速度20 m/s行驶时,在导弹命中目标大约5 s内所能到达最远的圆。分析可得,当坦克迎面向导弹前进时落角更易满足30°的约束,当坦克背离导弹前进时落角最难达到30°约束。所以只需要让最难满足落角约束的情况满足条件,那么其他情况(坦克无论向什么方向以多大速度均可)都会满足条件。所以之后将坦克速度按+20 m/s进行模拟。 假设导弹速度240 m/s,坦克速度20 m/s,坦克沿直线全速逃离导弹的情况下,初始r0=2 400 m,q0=30°,V=240 m/s,VT=20 m/s,K=4,根据数值进行仿真计算得出表1结果。 表1 仿真实例 (°) 当比例系数K不变,速度比p不变,可以根据不同初值q0求得最终目标线偏转角的范围,见表2。 表2 K=4,p=12时的落角预测 (°) 由表2可知,当要求满足落角大于30°约束时,初始目标线角应大于24°,这样最终加上最小偏转角Δqmin后为30.4°,满足落角约束条件。 表3 K=3,p=12时的落角预测 (°) 由表3可以看出,当要求满足落角大于30°约束时,初始目标线角应大于22°,此时加上最小偏转角Δqmin后为30.6°,满足落角约束条件。 将式(4)对时间进行求导,可得: (13) (14) (15) (16) (17) 因为η是从q0变化到0,逐渐减小,所以当η=0时,式(17)右端有最大值,比例系数K应大于右端最大值。 将η=0代入式(17)得到: (18) 图4 导弹过载曲线 可以发现在最初始阶段过载已经为5.6左右,超过预计的最大可用过载5。 将过载表达式(16)与法向运动方程(4)联立可得: (19) 因为nk≤nmax,可知比例系数K有上限,即 (20) 式中:rmax=3 000 m(导引头最大识别距离),g=9.8 m/s2,nmax=5,V=240 m/s,VT=-20 m/s,η=ηT=30°,经计算可得:K<4.712。 综上,比例系数K的范围应满足公式 (21) 在过载约束下影响导弹的落角主要有两个参数,一个是初始目标线角q0,另一个是转比距离r0。考虑到落角指标可根据落角预测模型得到,并且由于导弹受到过载限制,转比距离不能太小,所以在开始启动比例导引时,需用过载要小于等于最大可用过载,则可以按照导弹最大可用过载来估算转比距离。 由式(21)可得: (22) 在启动比例导引之前,导弹保持平飞,所以在初始时刻η=ηT=q0,可以得到: (23) 根据公式可以得到启动比例导引制导律的最小距离rmin,令比例系数K=4,nmax=5,经式(23)计算出最小转比距离r0,由于在落角预测中当K=4时得到初始目标线角大于24°时会满足最终落角要求,以初始目标线角q0为横坐标,r0为纵坐标,画出曲线如图5所示。 图5 K=4时最小转比距离与q0的关系 在图5蓝色曲线左上方的点,表示既满足落角要求,又符合过载约束的初始弹道参数,曲线右下方的点表示仅满足落角的要求,但是不满足过载约束。同理,可以画出当比例系数K=3时的最小转比距离r0与q0的关系,如图6所示。 文中根据理论分析得出落角公式,并建立落角预测模型。在计算弹道之前,仅根据初始值即可估算出落角的大致范围,对导弹平飞段的平飞高度有指导性的作用。在实例中结合过载约束,选取合适的比例系数K,得出导弹需用过载变化趋势。在给定最大可用过载的前提下,得出转比距离、初始目标线角之间的 关系,根据仿真图找出既满足的过载约束,又符合落角条件的参数r0及q0,同时以期望落角命中目标。该方法原理简单,工程上容易实现。但仍存在一些问题,如没有完全挖掘出导弹的潜力,该模型仅考虑了最难满足的落角要求,即目标远离导弹全速逃跑的情况,如果不是该情况,那么落角会更大,将会得到更好的击顶效果,这样会造成导弹性能的浪费。 图6 K=3时最小转比距离与q0的关系



1.5 比例系数K的范围

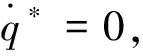
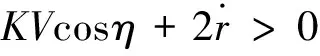
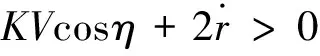

1.6 满足战技指标的初值范围
2 小结


