中学数学解题中联想思维法的应用
(上饶中学, 江西 上饶 334000)
心理学认为联想是通过感知目前的事物想起与之相关的其他事物的现象。在数学解题过程中,联想是一种帮助我们建立数学对象与有关知识间联系的桥梁。而人们在对事物发生认识时,联想思维是会在事物联系的基础上,形成一种由此及彼的思维活动,它在这过程中起着至关重要的关联作用。在探索一些未明的知识时,脑海中已有的知识会和这些知识发生关联,进而解决这些问题。在解决数学问题的过程中,需要先分析题目中已知的条件和想要得到的结果,进而思索到可以使用的法则、定理、公式,并在此基础上寻得解题的方法。文献[1-4]对中学数学如何解题进行了分析,文献[5]对如何教和学数学进行了讨论。本文将对中学数学中联想思维的培养方式及作用进行深入的研究。
1 中学数学题解题过程中联想思维法的作用
1.1 能使数学问题化表为里
数学知识是由很多基础知识构成的,但很多时候,解决问题的要点就在于这些基础知识上。


1.2 能使数学问题化繁为简
在解析几何中,书本上定义了平面上两点A(x1,y2),B(x1,y2)的距离:
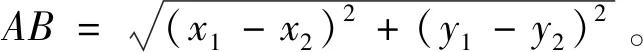
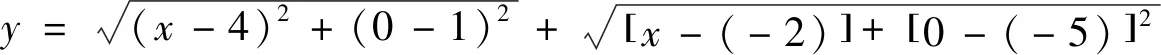
1.3 能使数学问题化堵为畅
爱因斯坦认为:科学研究最可贵的要素之一是直觉思维,与之类似的,直觉思维在解决数学问题时能帮助联想思维源源不断地涌出,使得我们在详细地分析问题后,不需要完整的推理,就能够触及问题的实质,进而能够预判。可以说联想是灵感诱发而产生的。当然,在碰到一些难以下手的数学问题时,我们也需要靠联想思维产生的灵感来将原本受阻的题目解决。
例2已知
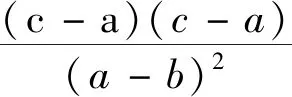
首先我们能很快看出这是一道在已知三者(a,b,c)关系的基础上,要求三者之间比例的题目。
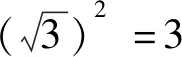
最后,我们再通过观察这个方程还有个根是1。故根据此思想,由韦达定理得到:
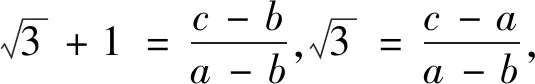
通过例2,我们可以发现在求解一些数学问题时,在联想思维的启发下,马上就能水落石出,拨云见日。
上述例子告诉我们,联想思维在解决数学问题中发挥着重要的作用。但联想思维并不是凭空而来的,是需要在具体解题中培养出来的。如何培养学生的联想思维解决数学问题是数学老师的主要任务之一。但学生之间,教学内容之间都存在着巨大的差异,要因材施教,我们要使用不同的教学方法。那么,怎样的教学才是有效的呢?下面介绍几种方法。
2 在中学数学解题过程中培养联想思维的方法
联想法拉近了数学题目中条件和结论的关系,它在解中学数学题时起着承上启下的作用。由于中学生思维发展还不太成熟,也就不能全面地看待问题。因此,我们需要合理地引导学生在解题时使用联想思维,把问题简单化。
2.1 举一反三,拓宽联想的空间
联想是产生直觉的先导。猜想则是在直觉的引导下产生的结果。而直觉是一种不需要在脑中进行复杂地思索,就能快速关联和整合已知的零星、单独的信息的一种思维活动,每个人关联和整合的能力各不相同,取决于个人的联想空间。因此,我们需要经常引导学生联想自己将要面临的问题。
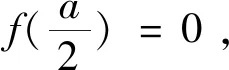
看到例题,我们能很快发现等式结构和三角不等式非常相似,在此基础上,我们可以联想到
cos(x+y)+cos(x-y)=2cosx·cosy。
再由f(x)联想到cosx,又由cos(π/2)联想到f(a/2)=0,最后,我们就能猜想π是类似于a,f(x)则是以2a为周期的函数。由此我们可以看出,合适的联想带来的直觉常常可以帮助我们更快地解决问题。这给我们数学教学带来启示——在教学中应充分注重培养学生思维的形式。
2.2 启迪直觉,探求数学美
数学简单性、对称性、统一性就是我们常说的数学美。我们在做题时如果能够将数学问题的特征与数学美感相结合,大脑就能在已有知识经验的基础上不假思索地产生审美直觉,帮助我们大致地确定解题的基本方向。
例4如实数x,y满足等式(x-2)2+y2=3。那么y/x的最大值是多少?
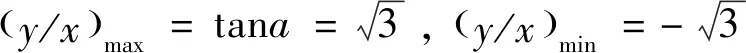
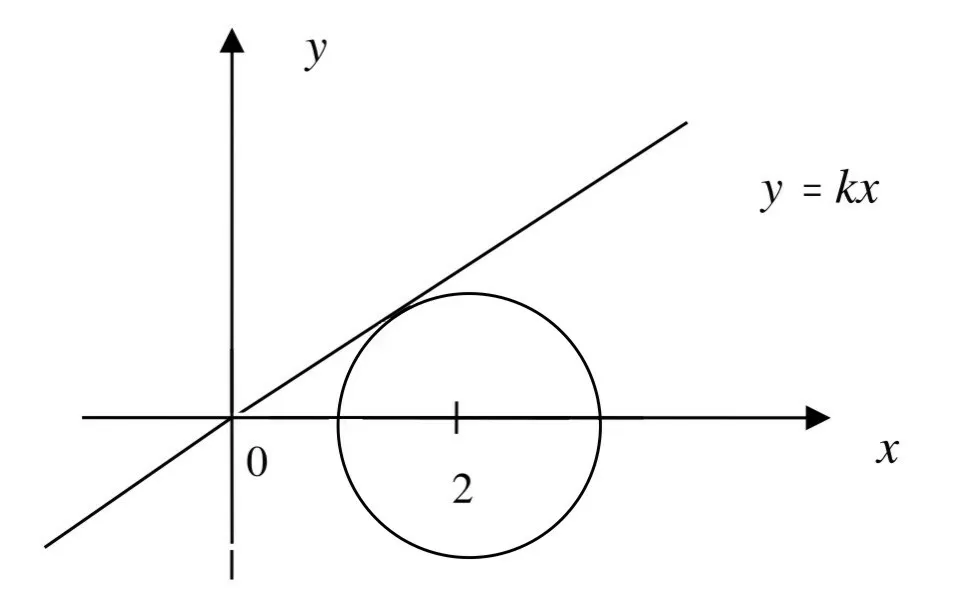
图1 y/x与直线y/kx的关系
3 几种常用的联想思维方法的应用
联想思维是求解数学题的基本思考方法之一。已知和未知间的联想就是解决数学问题思维本质。但这种联想并不能清楚地推理出,因此,我们在解题时,需要先进行观察,有时还需要画出相应的示意图,再根据条件联想到与解题相关的解题方法,进而找出条件与结论之间的内在联系,最终得到解题的思路。下面举例说明。
3.1 贴近联想
从问题或者问题中的部分想象到与之同样或相近的思维方法叫做接近联想。例如,从“双曲线上的点到两个焦点的距离”联想到使用“双曲线的定义”。
例5设双曲线x2-y2=1的两个焦点分别为A1、A2,点P在双曲线上,且满足∠A1PA2=900,则ΔA1PA2的面积是( )?A.1 B.2 C.3 D. 4
(1)通过分析可以看到:点P到两焦点A1和A2距离是ΔA1PA2上的两边PA1和PA2。(2)可以联想到:双曲线的定义(接近联想),|m-n|=2a(设|PA1|=m,|PA2|=n)。(3)可以看到:ΔA1PA2是直角三角形,问题与其三边有关。(4)进一步联想到:勾股定理:m2+n2=(2c)2(贴近联想)。(5)可以看到:结论是求S=m·n。(6)最后联想到:把|m-n|=2a平方,可出现mn,再利用2m+2n=2(2c),即得,m·n的值。从而得到选项A的结果。
3.2 相近联想
通过问题中的条件或结论,联想到与它相似的知识并解决问题的方法叫做相似联想。如,(1)看到x+y+z=xyz形式的式子,联想到在非直角△ABC中:tanA+tanB+tanC=tanAtanBtanC,从而设x=tanA,y=tanB,z=tanC来解题;(2)看到“a2+b2”联想到“复数的模”“勾股定理”“点(a,b)到原点的距离”“圆的方程x2+y2=r2”,并利用这些知识来解决这个问题,等等。
3.3 反向联想
具有对立关系的数学对象之间的联想叫做逆向联想。如果碰到难以想到对立面的复杂结论,我们就需要对此结论的对立面进行分析、化简,进而解决问题。例如,由“x>0”联想到“x≤0”;由“至少有一个实根”联想到“无实根”;由“同一平面内两条直线相交平行”联想到“同一平面内两条直线相交”等。
例6已知在三个方程x2+4ax+3-4a=0,x2+(a-1)x+a2,x2+2ax-2a=0中至少有一个方程有实根,求实数a的取值范围?
分析:结论中的“三个方程中至少有一个方程有实根”,如果直接解就要各种类别讨论,情况较多,容易遗漏。此时联想到它的“反面”。由此把问题转化为:“三个方程全无实根”易解决,即:Δ1<0且Δ2<0且Δ3<0,解得-1 在传授学生解题方法时,为了帮助学生理解知识,激发学生的积极性,需要尽可能地鼓励学生通过不同的角度进行联想。但培养联想能力光这样还不够,拥有踏实的基础知识和基本技能也是必要条件,否则与问题相似的知识很难在脑中被搜索出来。4 总结

