基于改进区间摄动分析的统计能量分析法

张 政，许孟辉

（宁波大学 机械工程与力学学院，浙江 宁波315211）

统计能量分析(Statistical Energy Analysis，SEA)可以有效克服有限元法、边界元法等在解决复杂系统宽带高频动力学问题中遇到的困难[1-2]。它将复杂系统划分为多个具有相似模态的耦合子系统，利用统计学方法以能量描述系统状态及动响应。然而，以SEA 进行动力学系统的环境预示需要确定3类参数：子系统的模态密度与内损耗因子、子系统间耦合损耗因子。以内损耗因子为例，其10%的误差导致响应估计1 dB 的偏差，其100%的误差导致响应估计3 dB的误差[2]。然而，内损耗因子通常为10-2～10-4数量级的小数，耦合损耗因子的数量级则更小，在工程领域内对这些小数量级参数进行高可靠度的试验测量是非常困难的。同时，系统服役环境亦非一成不变，这将导致材料参数、边界参数等的变异。因此，SEA 参数具有明显的不确定性[3-4]，快速准确计算输入参数的不确定性对子系统能量及其对动响应的影响规律的分析是十分必要的。

Culla等[5]研究了随机参数对SEA功率流平衡方程的影响。在系统参数可用数据不足的条件下，高精度地拟合随机参数分布难以实现，而以非概率凸模型对不确定性参数建模具有突出的优势。Yin等[6]结合有限元法、SEA 与区间摄动分析法(Interval Perturbation Method，IPM)研究了区间参数对中频声振耦合分析的影响规律。吴迪等[7-8]将不确定性以区间参数和非概率凸模型参数定量化，基于Taylor级数展开法研究了认知不确定性对结构振动子系统间能量流的影响。本文作者也对区间参数系统的高频动力学特性分析提出了逐维法和顶点法[9]，但这两种方法的计算效率低于IPM。虽然定量度量系统参数的不确定性对分析其高频动力学特性的影响规律具有重要的理论价值和工程意义，但不确定性在SEA 中的传播分析研究相对有限，且现有方法面临计算精度(如Taylor级数展开法)或计算效率(如逐维法和顶点法)的限制。

本文以区间参数向量对不确定性建模，基于IPM 高效率的优势，通过保留部分高阶摄动项克服IPM 计算精度不足的限制，提出基于改进区间摄动分析(Improved Interval Perturbation Method，IIPM)的统计能量分析法(IIPM-SEA)，通过与蒙特卡洛法、顶点法与经典IPM法的比较验证本文方法有效性。

1 SEA基本原理与方程

SEA 使用统计模态的概念，以振动能量作为描述系统振动的基本参数，利用各子系统间的能量流关系式对结构振动与声辐射等系统动力学特性进行时间与空间上的统计评估。SEA的基本假设包括：

(1)子系统间为线性保守耦合，不存在非保守性的耦合，且满足互易性原理；

(2)子系统间能量流与子系统间实际能量差成正比，即能量流与平均模态能量之差成正比；

(3)系统受互不相关的宽带随机激励作用，具有模态非相干性，且可进行能量线性叠加。

对于由N个子系统组成的系统，SEA 功率流平衡方程为

其中ηi(i=1,2,…,N)为子系统i的内损耗因子，ηik(i≠k＆i,k=1,2,…,N)为振动能量从子系统i传至子系统k的耦合损耗因子，Pi,in(i=1,2,…,N)为外界对子系统i的输入功率，ω为分析带宽的中心频率，Ei(i=1,2,…,N)为分析带宽内子系统i的能量。功率流平衡方程的矩阵格式写为

其中损耗因子矩阵L为

能量列向量E为

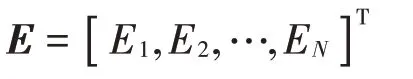
输入功率列向量Pin为

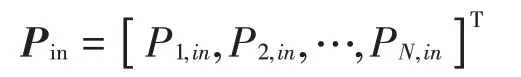
上标T为转置运算符。

根据式(2)表示的功率流平衡方程，若已知各子系统的模态密度与内损耗因子、子系统间耦合损耗因子及外界激励输入功率，通过代数运算可获得每个子系统的平均能量，进一步获得诸如振动速度与声压等响应。但如前文所述，模态密度、内损耗因子、耦合损耗因子与外界激励等参数不可避免地存在不确定性，导致各子系统能量及其动响应具有分散性。针对这个问题，下文提出一种用于定量度量参数不确定性对系统动响应影响规律的方法。

2 区间参数系统的统计能量分析

2.1 问题描述

系统参数以向量a表示，式(2)中SEA 功率流平衡方程进一步写为

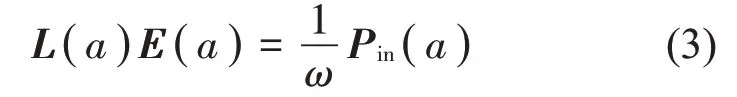
在系统参数a可用数据不足的前提下，系统参数的不确定性可通过区间向量建模，以aI表示。因此，区间参数系统的SEA功率流平衡方程为

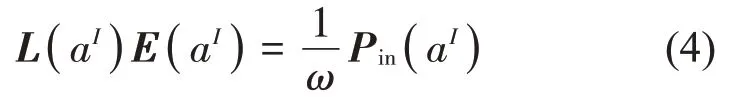
其中区间参数向量aI的下界向量和上界向量分别表示为aL和aU，即

方程式(4)的解为

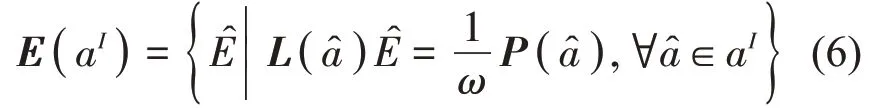
值得指出的是：(1)各子系统的能量因共享系统参数a而相互依赖，式(6)表示的解集通常极难精确计算；(2)工程领域更为关心每个子系统能量及动响应的变化规律或界限。因此，区间分析以获得式(4)或式(6)的最小超立方体包络解为目标，即

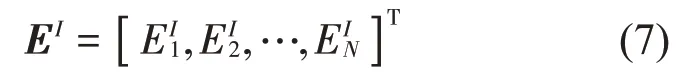
其中

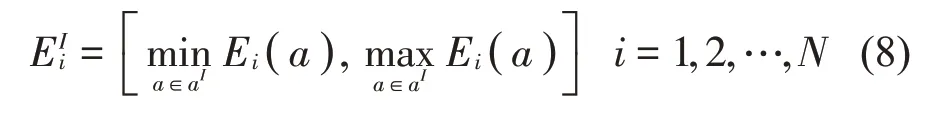
2.2 基于改进区间摄动分析的统计能量分析

区间摄动分析法是一类经典的区间分析算法，因其计算效率高而备受青睐，该领域研究集中于如何提高其计算精度。从发展历程看，区间摄动分析法可分为3种格式，即Qiu-based IPM[10]、McWilliambased IPM[11]、IIPM[12-13]。从计算精度而言，Qiubased IPM 具有明显的“区间过估计”效应；McWilliam-based IPM具有一定的“区间平移”效应，计算精度高于前者；IIPM 具有一定的“区间不可预估”效应，较前两者的计算精度为高，但其存在计算格式不合理的问题。本文分析现有IIPM的局限，提出合理的IIPM 计算格式，进一步建立基于IIPM 的统计能量分析方法。

区间向量aI的中点ac与半径ar分别为

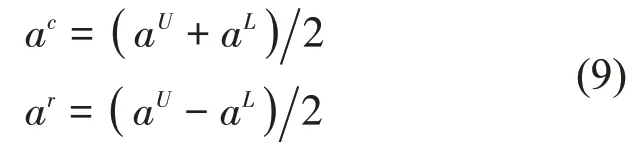
将损耗因子矩阵L( aI)和输入功率向量Pin(aI)在ac处进行Taylor级数线性展开，有

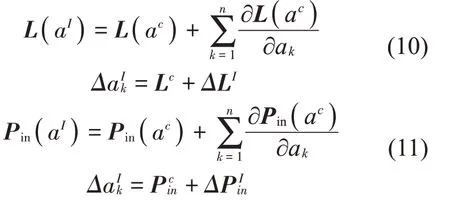
其中

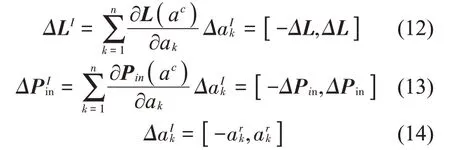
根据式(4)可知区间参数系统的区间能量矩阵为

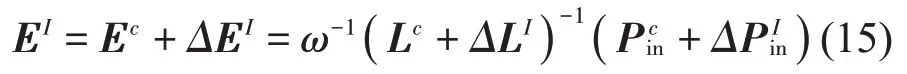
当ΔLIL-1谱半径小于1时[12-13]，(Lc+ΔLI)-1可以展开为Neumann级数，有

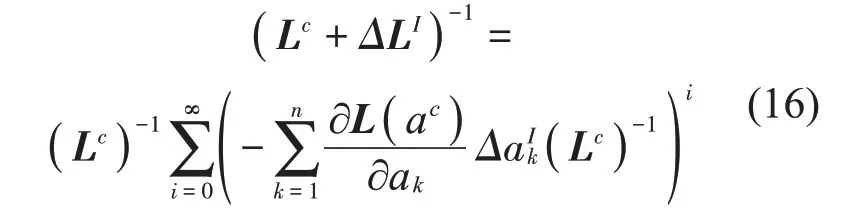
令

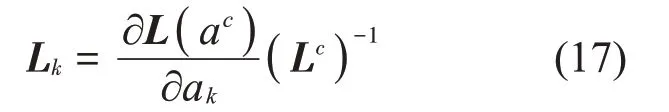
从而，式(16)化简为

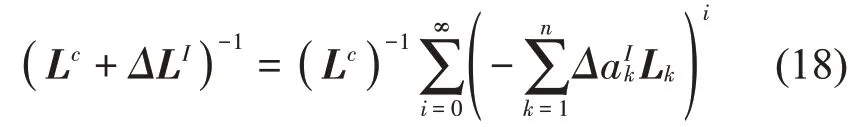
而级数和的幂次项可以表示为

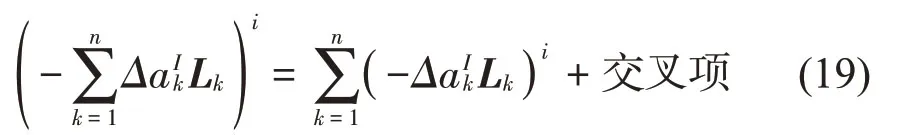
忽略式(19)中的交叉项，式(18)进一步化简为

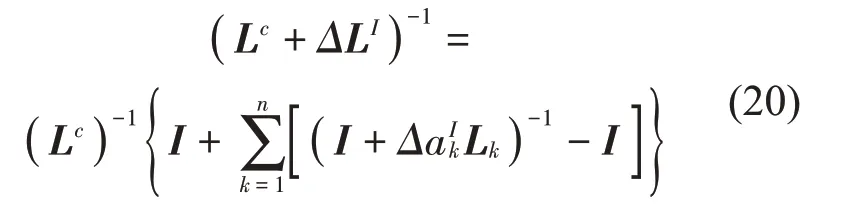
其中I为单位矩阵。令

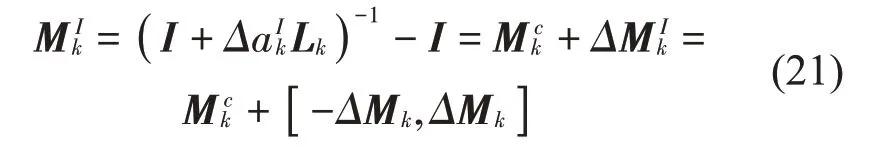
其中

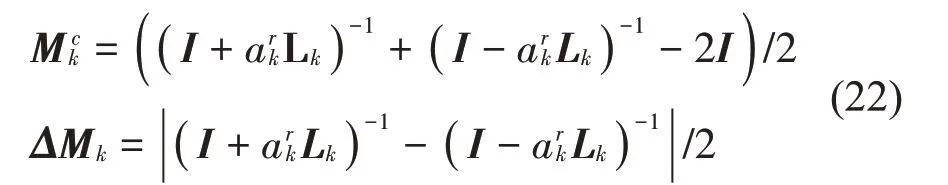
从而，式(20)进一步化简为

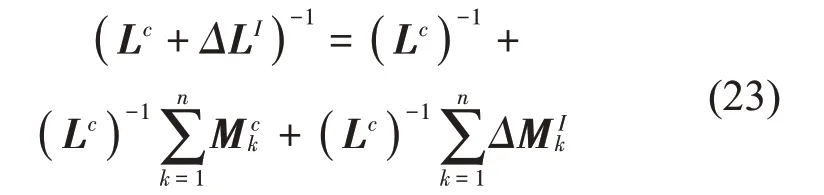
将式(23)代入式(15)中，有

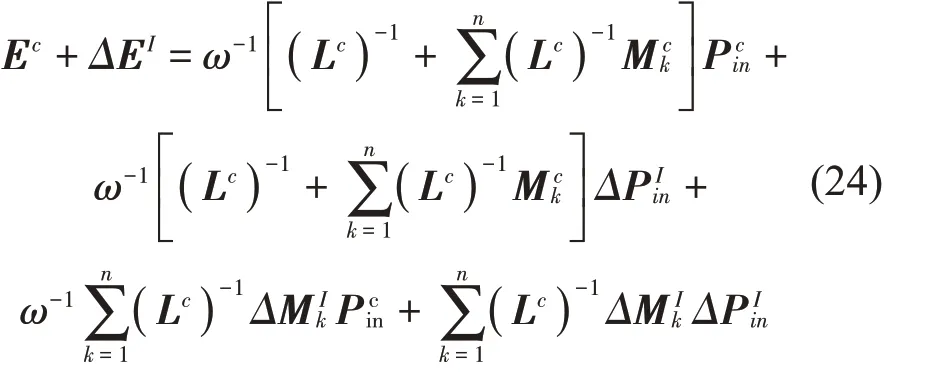
忽略式(24)中的二阶摄动项，有

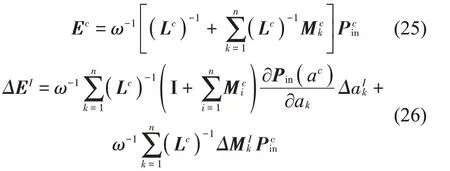
现有IIPM 根据式(25)给出的区间能量向量EI的区间半径ΔE分别为

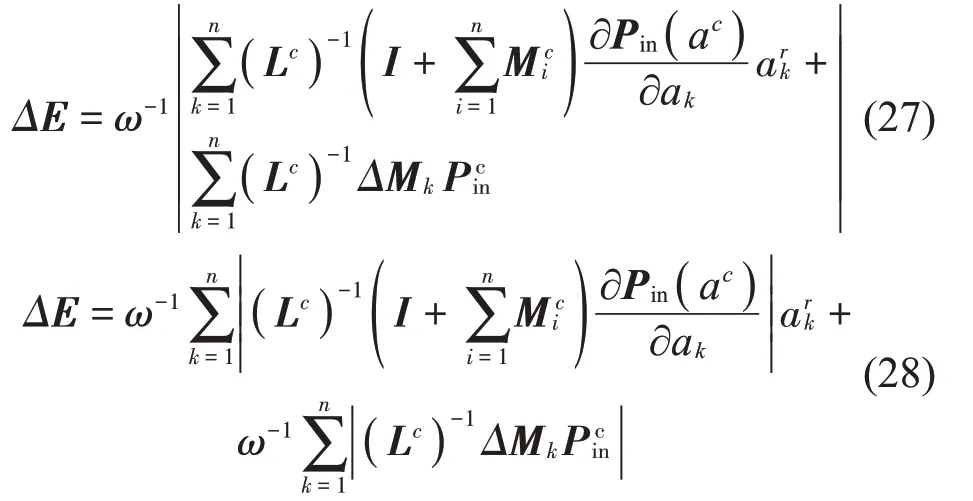
在式(26)中有两类区间变量，即ΔaIk和ΔMIk，因式(22)的关系，这两类区间变量是相互独立的，且ΔMIk中各区间变量分量也是相互独立的。进一步地，由式(26)可知，ΔEI是ΔaIk和ΔMIk的线性函数，ΔEI的区间界可以通过顶点法精确获得。因此，式(27)和式(28)忽略了2 个事实：(1)能量向量EI不同分量的区间界可在区间变量张成子空间的不同顶点处取得；(2)能量向量EI任一分量的区间界并非总在区间变量右端点取得，其仅是区间变量张成子空间的一个特殊顶点。为清晰起见，以如下形式简单的矩阵和向量来说明，即令

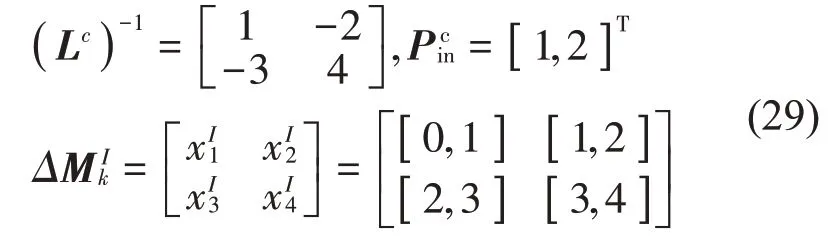
从而，E1I= ( Lc)-1ΔMkIPicn的精确区间界为

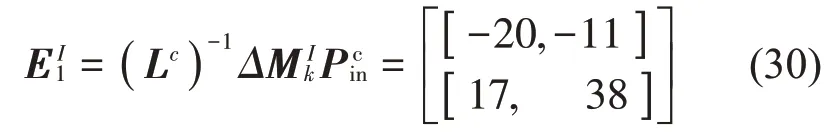
在由ΔMkI中区间变量xI=[xI1,xI2,xI3,xI4]张成子空间内，以式(30)所表示精确区间界的上界EU1为例，与它2个分量所对应的空间顶点是

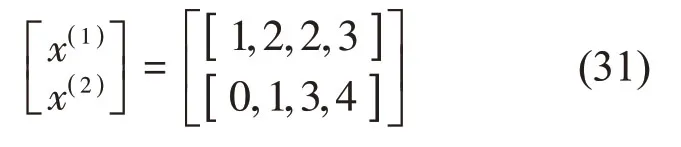
由式(31)可知，E1I中2 个区间分量分别在顶点处取得，且这2 个顶点均不是区间变量xI的右端点。然而，式(27)和式(28)均认为能量向量EI各分量区间界在区间变量张成子空间内的同一个顶点处，即区间变量右端点取得。

因此，能量向量EI的区间半径ΔE为

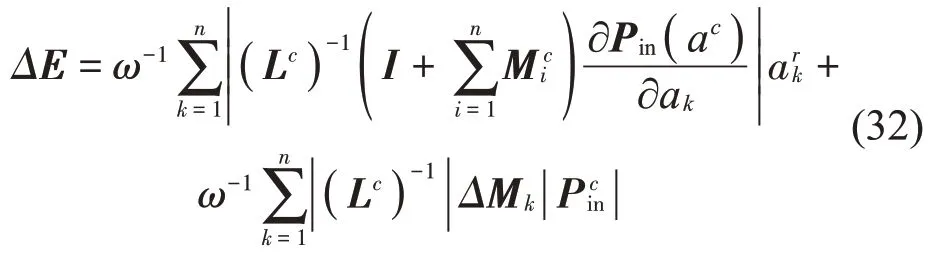
根据式(25)和式(30)获得系统能量向量的区间界为

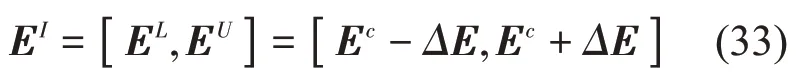
值得指出的是，本文方法以SEA 为基础，满足SEA假设前提下可通过所提方法获得系统参数不确定性对系统响应的定量化影响规律，即：较SEA 而言，本文方法对响应频率范围等因素无附加要求。但就不确定性分析而言，本文方法适用于小区间参数输入问题，其适用范围可通过子区间方法得以有效拓展。

3 算例与讨论

考虑图1中板腔系统，它由1个四边简支矩形铝板与5个刚性壁面围成，板长L、板宽W与板厚t在图中标识，该系统区间参数列在表1中，其中ρs、Es、vs和ηs分别为铝板的质量密度、弹性模量、泊松比和内损耗因子，ρa和ηa分别为声腔内声学介质的质量密度和内损耗因子，矩形铝板上表面的几何中心点的位置作用白噪声机械激励。

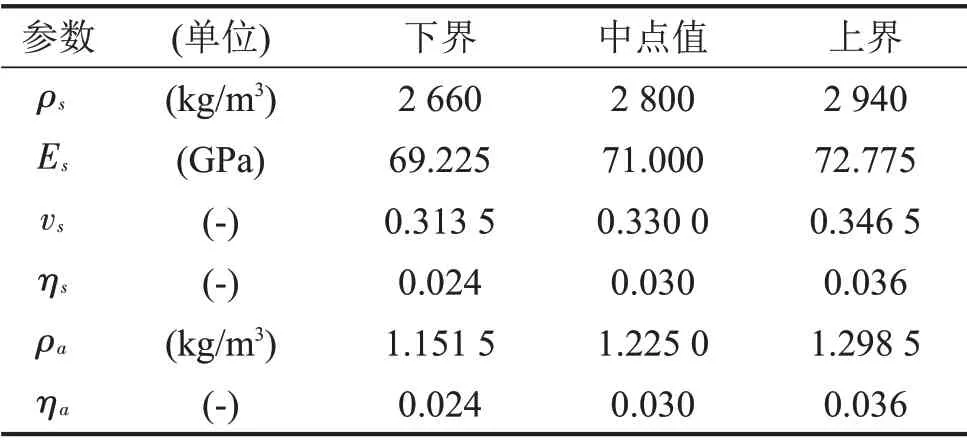
表1 板腔系统的区间参数

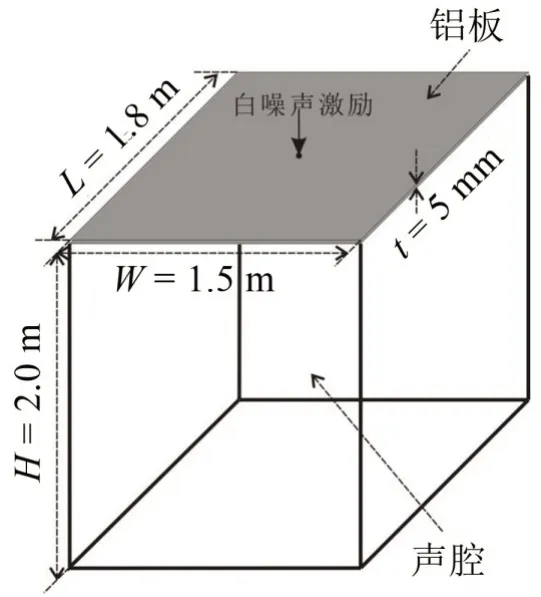
图1 板腔系统构型

板腔系统的SEA 模型如图2所示，在给定区间参数任意实现的条件下，平板子系统的能量与声腔子系统的能量可以通过式(1)中的经典功率流平衡方程计算获得。

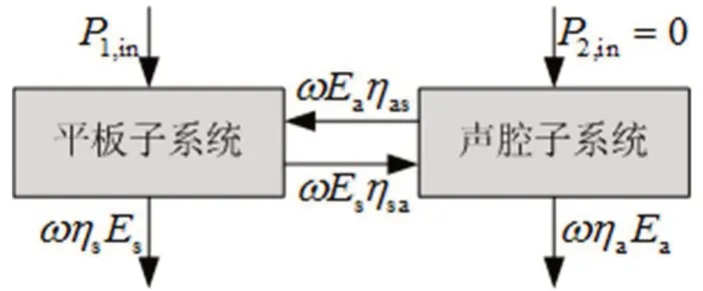
图2 板腔系统的统计能量分析模型

根据铝板子系统能量计算得到铝板振速级VSL

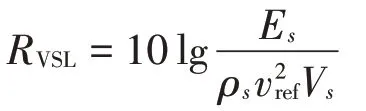
其中Es为铝板子系统的能量，ρs为铝板质量密度，Vs为铝板体积，vref为参考速度，取为

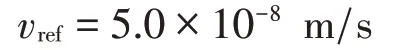
相应地，声腔内声压级SPL 根据声腔子系统能量计算得到

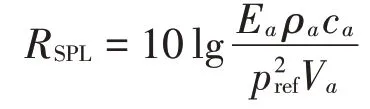
其中：Ea为声腔子系统的能量，ρa为声腔内介质的质量密度，ca为声腔内介质的声速，Va为声腔体积，pref为参考压强，取为

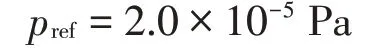
采用区间摄动分析法(McWilliam-based IPM)、所提方法(Proposed method)、蒙特卡洛法(MC)和顶点法(Vertex method)计算平板子系统和声腔子系统能量的区间界。根据区间扩张原理，铝板区间振速级/声腔区间声压级的下界和上界分别为

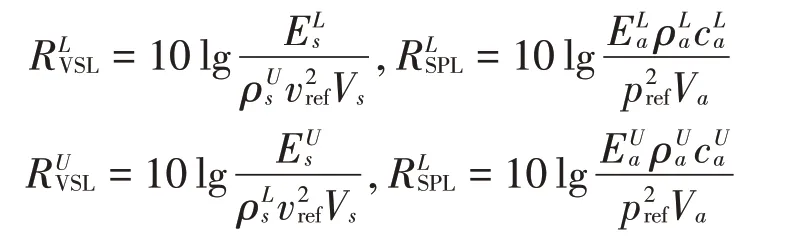
其中声学介质中声速与声学介质密度是相关的，其下界和上界分别为

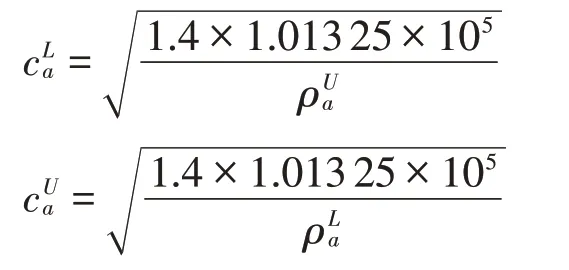
铝板区间振速级频响分布和声腔区间声压级频响分布分别如图3和图4所示。

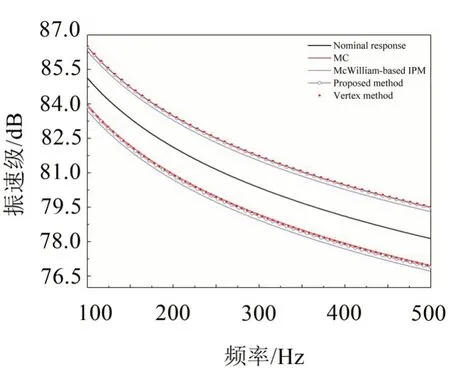
图3 铝板振速级的区间界

可以获得结论如下：

(1)顶点法与蒙特卡洛法计算的区间界基本吻合，且前者略宽于后者。因这两种方法均源于抽样策略，二者计算的区间界为精确区间界的子集，因此，在该问题中顶点法计算精度高于蒙特卡洛法。进一步地，顶点法需运行64 次传统SEA 模型，其计算效率随区间参数个数的增加而指数递减，此例中蒙特卡洛法运行传统SEA模型次数为106；

(2)与顶点法计算结果相比，经典区间摄动分析法的计算结果存在明显“区间平移”现象。相比而言，本文方法可以减小“区间平移”效应，计算精度高。且本文方法仅需7 次SEA 分析过程，其计算效率随区间参数个数的增加而线性递减，显著高于顶点法的计算效率。与顶点法相比，本文方法以其计算精度极小幅度的牺牲为代价大幅度提高了计算效率。

4 结语

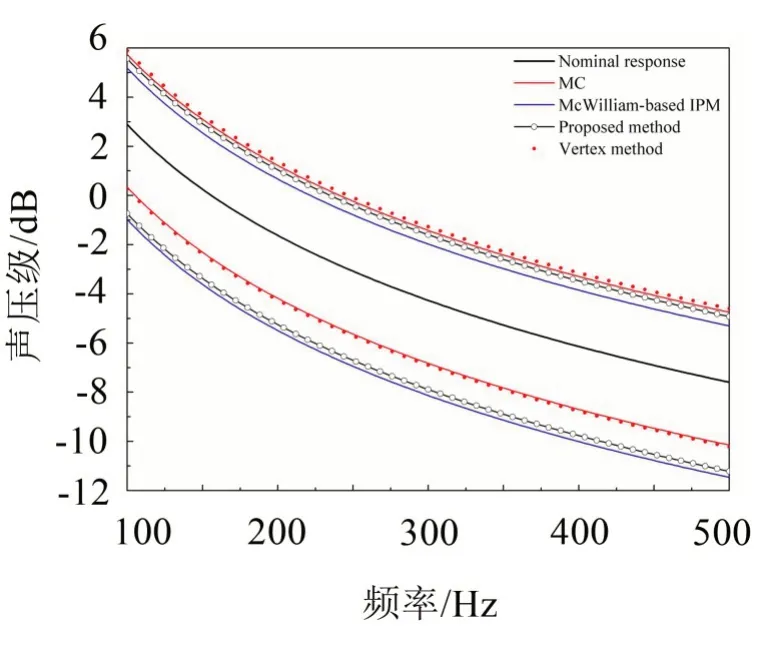
图4 声腔声压级的区间界

在统计能量分析过程中，耦合损耗因子的不确定性源于系统几何参数波动、系统材料参数变异与试验测量误差，内损耗因子的不确定性源于试验测量误差。为定量获得内损耗因子与耦合损耗因子的不确定性对系统高频动力学特性的影响规律，本文以区间参数对系统参数的不确定性建模，对现有改进区间摄动分析法中区间响应的计算过程进行了合理改进，并与统计能量分析法相结合提出了一种基于改进区间摄动分析的统计能量分析法。主要结论包括：

(1)从计算精度看，本文方法因有效减小经典区间摄动分析法的“区间平移”效应而较后者具有更高的计算精度，但所提方法的计算精度低于蒙特卡洛法和顶点法；

(2)从计算效率看，本文方法与经典区间摄动分析法具有相同的计算效率，均随区间参数个数的增加而线性递减，且计算效率显著高于顶点法；

(3)本文方法可以高效准确地定量系统参数的不确定性对系统高频动力学特性的影响规律。与基于现有区间分析的统计能量分析法相比，本文方法在确保满意计算精度的前提下具有计算效率方面的优势。