自适应控制系统中矩阵解耦控制算法研究

高伟鹏，贺 国，刘树勇，杨理华

（1.海军工程大学 动力工程学院，武汉430033； 2.海军潜艇学院 动力系，山东 青岛266199）

对于船舶机械设备的振动问题，被动隔振无法消除旋转机械造成的线谱，且工况复杂，无法进行精确建模，常规的控制手段减振效果不明显。自适应主动控制的基本原理是直接在结构上附加作动器，通过自适应律调节控制输出信号，驱动作动器产生相反的力抵消初级振动[1-2]。与传统的控制手段相比，自适应方法在控制具有时变特性的低频线谱振动上有独特的优势[2]。在实际的控制系统中，单一的作动器难以满足振动控制的需求，需要多个作动器来扩大范围，即需要采用多通道自适应控制算法（MFxLMS）。但MFxLMS 存在许多局限，例如时延大、参考信号难以提取、通道耦合等问题。

国内外学者对MFxLMS 算法进行了很多研究。文献[3]提出了一种模块化的LMS 框架自适应算法来进行多通道的LMS FIR 滤波，即多变量系统的辨识。文献[4-5]中讨论了在频率跟踪的基础上对振动影响进行控制以及引进Sigmoid 函数约束优化控制器权系数抑制输出饱和问题，显著改善自适应控制器的性能。文献[6]中讨论了多通道FURLS算法，克服了空间宽带噪声收敛速度慢的问题，消除了声反馈对系统稳定性的影响。文献[7]讨论了窄带多通道Fx-Newton 控制算法，其迭代矩阵的特征值均接近1，可获得最佳的收敛速度。文中主要针对MFxLMS 的通道耦合问题进行研究，传统自适应方法多通过集中式控制实现解耦，简单的集中解耦运算量大，稳定性差，微小的波动可能会使控制器沿着错误的方向收敛，从而导致控制发散[8-9]。

针对通道数较少（n＜4）的控制系统，提出一种矩阵解耦优化算法。其原理是基于前馈补偿在次级通道矩阵前插入解耦优化矩阵，实现控制信号与误差信号的一一对应，此时控制系统等效为多个单回路，系统稳定性和收敛速度均有所提高。同时，为了增强作动器与临近传感器之间传递函数的作用，解耦矩阵主对角元素取为1，并给出解耦矩阵在工程实现时的具体计算方法。通过双层隔振平台的仿真和试验对矩阵解耦优化算法进行验证，控制效果明显。

1 多通道主动控制系统

多通道主动控制系统中控制信号要经过多路次级通道才能到达误差传感器，每一个误差传感器采集的信号包含所有控制信号对该传感器的输出。

文中所探讨的多通道主动控制系统包含一个参考信号、N个作动器和N个误差信号。即存在N×N误差通道，其响应函数S(n)均用长度为M的FIR滤波器表示。控制滤波器w(n)设为长度为L的FIR滤波器。参考输入信号、期望信号、误差信号、控制信号分别为X(n)、D(n)、E(n)、Y(n)，上述信号在多通道控制算法中均为N阶向量。控制器权系数矩阵和次级通道传递函数矩阵分别为W(n)和S(n)。参数可表示为

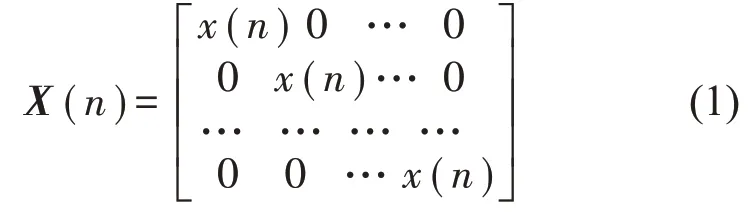
其中：

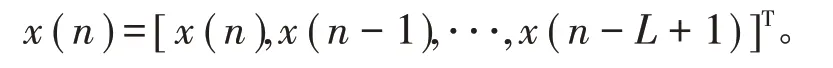
次级通道传递函数矩阵为S(n)，维度为N×N。

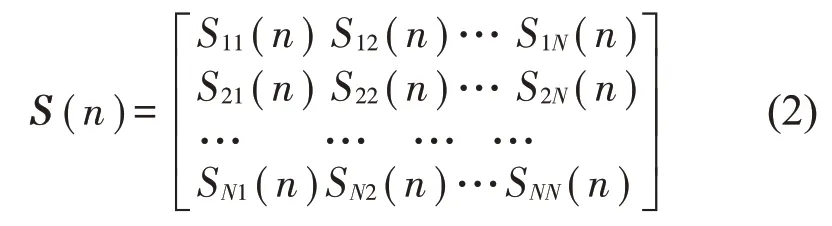
每一个Sij(n)表示第j个作动器对第i个误差传感器之间的次级通道传递函数。

多通道自适应控制的算法框图如图1所示[10-12]。

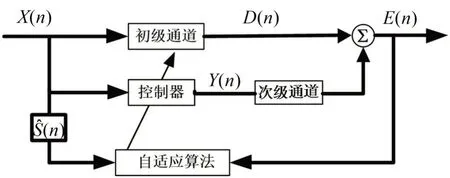
图1 多通道自适应算法框图

由图1可得

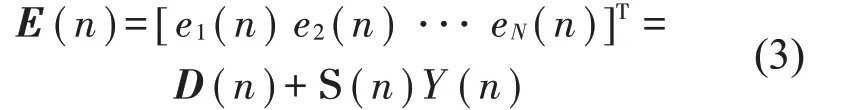
其中：

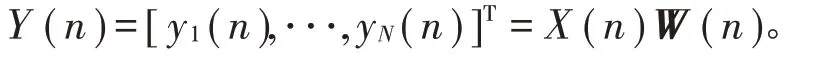
误差信号分量形式可以表示为

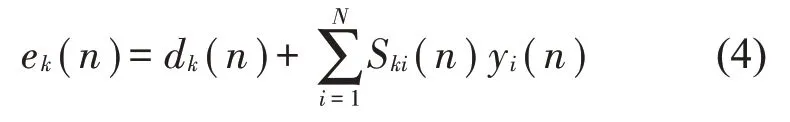
注意，式(4)中的yi(n)=wTi(n)x(n)得到的是第i个控制滤波器的输出。wi(n)为第i个控制器权系数，其长度为L

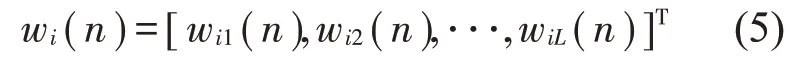
多通道控制算法的目标函数为

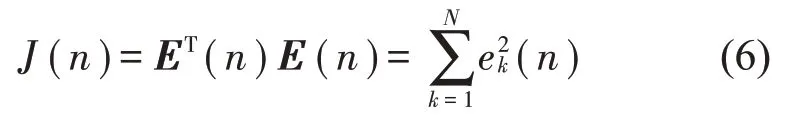
根据最陡下降原理，得到控制滤波器迭代更新算法如下

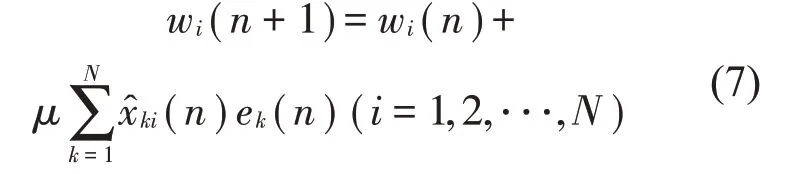
2 解耦矩阵的构造与工程实现

2.1 解耦矩阵的构造

根据前馈补偿原理，构造解耦矩阵使次级通道传递函数矩阵的非对角元素为0，实现完全解耦，解耦后的系统等效为多个单回路，输出信号与误差信号之间实现一一对应。为了减小解耦矩阵的计算复杂程度，本文构造的解耦矩阵H(n)对角元素均为1，使其在频率范围内满足

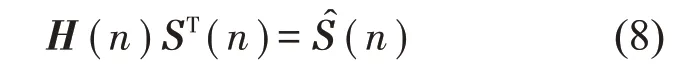
这里为对角矩阵，具体可表示为

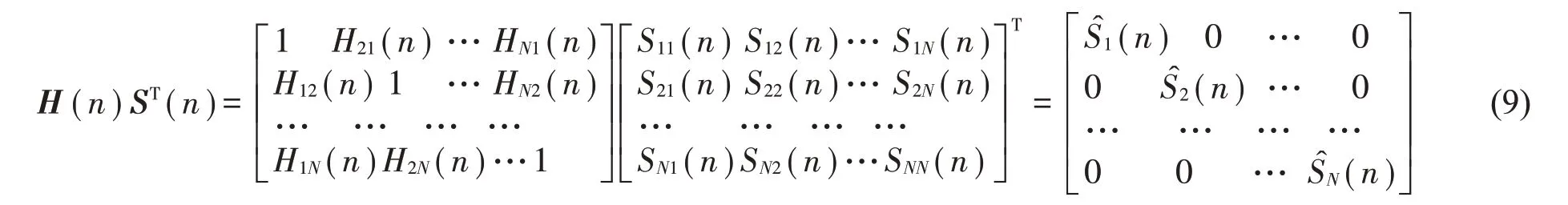
以三通道主动控制系统为例，插入解耦矩阵后，控制算法框图如图2所示。

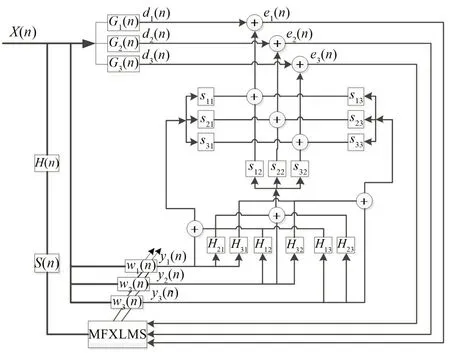
图2 三通道矩阵解耦控制算法框图

由图2可得，解耦矩阵的作用相当于是把单一控制器输出互相叠加到其他控制输出信号上，以此来抵消其他控制信号对本通道的影响。将新的误差通道传递函数矩阵变为对角阵，这里用频域表示，则有

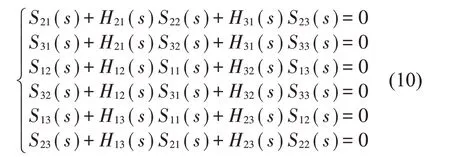
求解可得

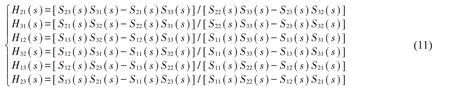
解耦矩阵H(s)为

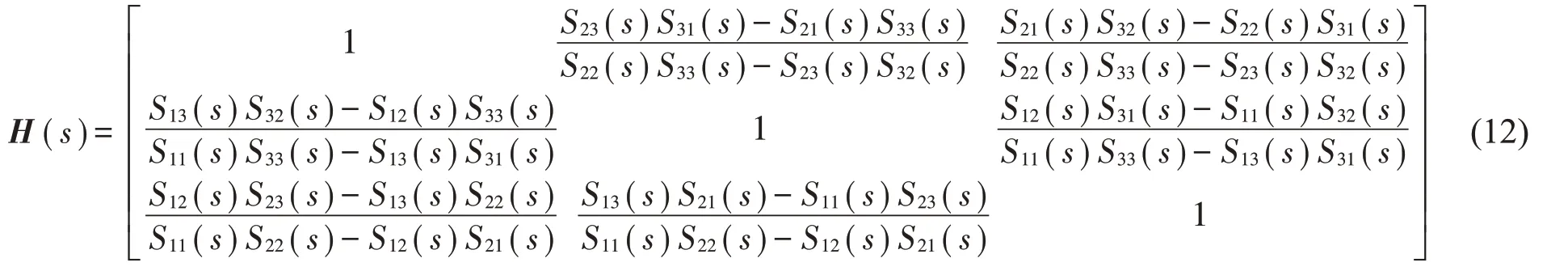
2.2 解耦矩阵的工程实现

由式(12)可以看出，解耦矩阵的频域表示H(s)中包含传递函数“乘”、“逆”等复杂运算，而对于文中所涉及到的具体工程应用，次级通道的传递函数以滤波器抽头系数来表示，长度为M。

传递函数的“乘运算”在时域内转化为2个滤波器抽头系数的卷积，为进一步简化计算，取卷积中心数据长度为M的数值作为卷积计算结果；非对角元素Hij(n)此时可看作2 个列向量“相除”，在MATLAB中进行运算，得到M×M矩阵，取出其中不为零的一列作为Hij(n)的计算结果，则Hij(n)最后的计算结果为一个长度为M的列向量。

重复以上步骤，得到解耦矩阵H(n)的时域解，实现解耦矩阵的工程应用。整个解耦矩阵的计算是在次级通道离线辨识的基础上完成的，没有额外增加控制过程中的计算量。且简化计算后解耦矩阵非对角元素的长度与辨识滤波器长度一致，均为M。

此时，插入解耦矩阵后，新的次级通道矩阵可表示为

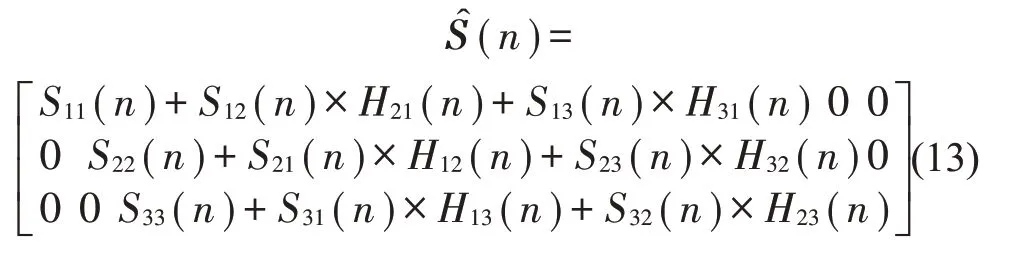
这里，为减小计算量便于控制过程的工程实现，Sij(n)与Hij(n)卷积运算时也取卷积中心数据长度为M的数值作为运算结果，则中主对角元素的长度为M。

通过插入解耦矩阵，系统可大致等效于多个单回路。某个控制器权系数的更新只跟对应的误差信号有关，大大减少了控制系统的计算量，提高了算法的稳定性。

3 仿真与试验研究

以双层隔振试验平台为研究对象，对矩阵解耦优化算法进行仿真与试验验证。系统含有1个参考信号传感器，3 个电磁作动器（第4 个作动器起承载作用）和3 个误差信号传感器。作动器与中层加速度传感器之间即为物理次级通道，以试验测得的9组次级通道数据作为仿真中的次级通道模型，对含有白噪声的双频线谱进行控制。

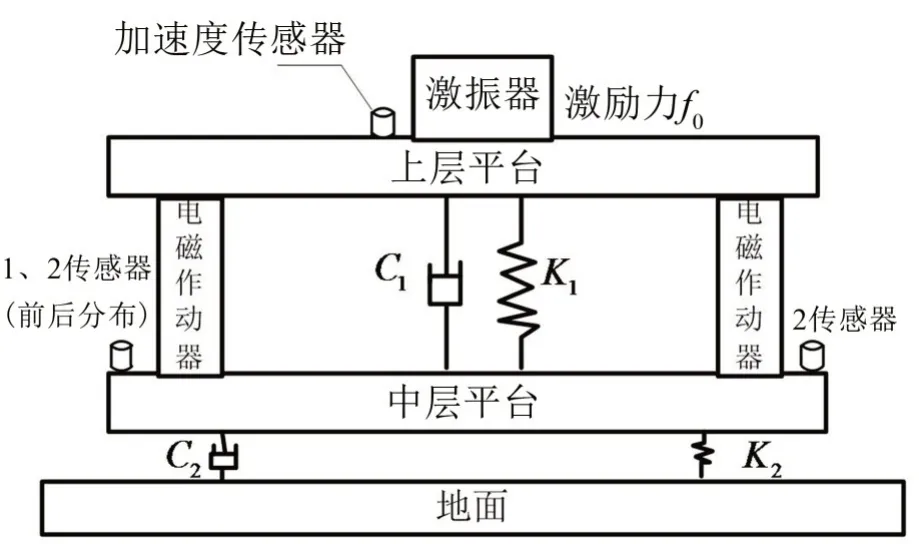
图3 多通道双层隔振系统模型

3.1 误差通道辨识

为了得到控制试验中较为精确的次级通道模型，利用20 Hz～150 Hz的白噪声依次激励4个作动器，采样频率为2 kHz，采用横向滤波器作为辨识模型（以横向滤波器来逼近误差通道传递函数），阶数设为128。部分误差通道的辨识结果如图4所示。

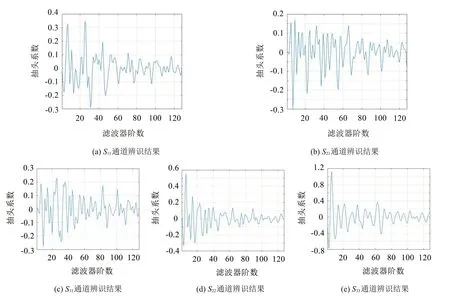
图4 误差通道辨识结果

辨识结果用横向滤波器表示，横坐标代表滤波器阶数，纵坐标为每1 阶对应的抽头系数。图4中图4(a)、图4(b)、图4(c)分别代表了1号作动器与1号传感器、2号传感器和3号传感器之间的误差通道辨识结果，不难看出1号作动器与1号传感器之间的误差通道辨识系数较大，符合客观事实。同理，图4(d)、图4(e)为2号作动器与2号传感器、3号作动器与3号传感器之间的误差通道辨识结果。

3.2 多通道控制仿真

将上述辨识得到的误差通道放在Simulink控制模型中，进行三通道主动控制仿真。模拟参考输入信号为40 Hz 与60 Hz 的双频信号叠加高斯白噪声而成。

实际的误差通道矩阵为

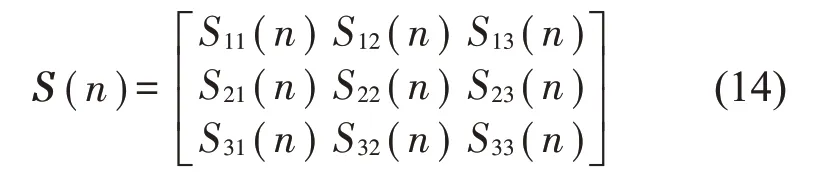
由S(n)构造解耦矩阵H(n)，其主对角线元素为1，将解耦矩阵置于控制信号之后；用新的次级通道矩阵对参考信号滤波。矩阵解耦控制仿真程序如图5所示。

控制迭代步长为5×10-5，控制滤波器长度为300阶，对不考虑通道耦合和矩阵解耦优化两种情况分别进行控制仿真，结果如图6、图7所示。

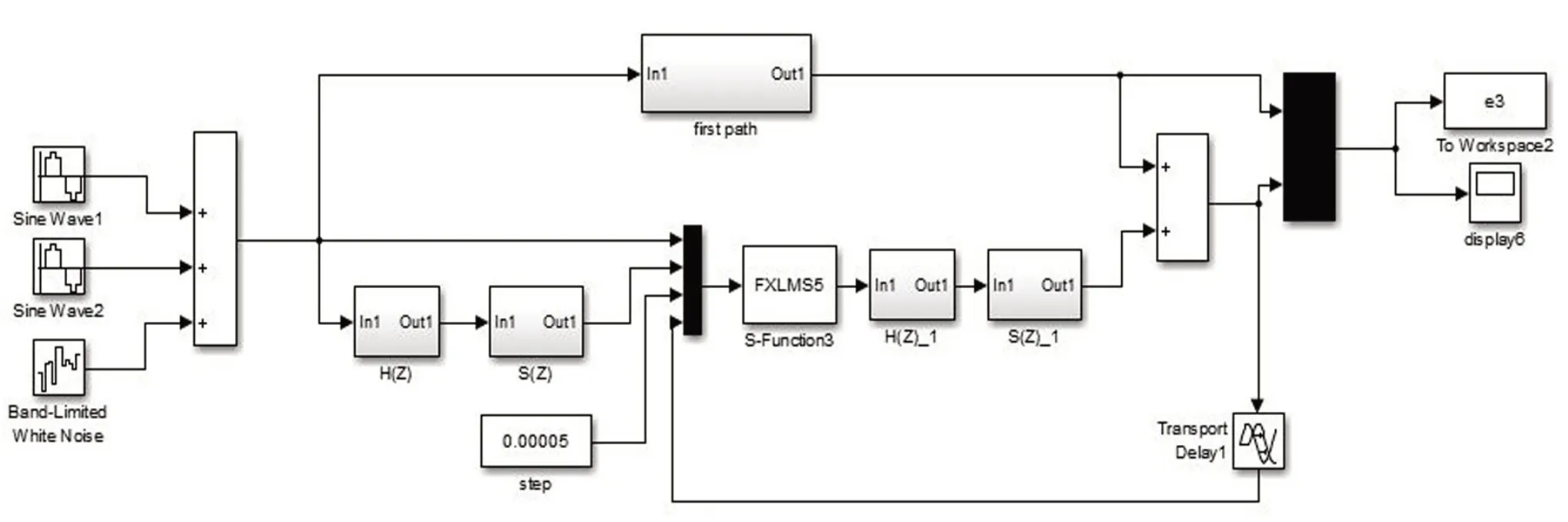
图5 矩阵解耦控制仿真程序图

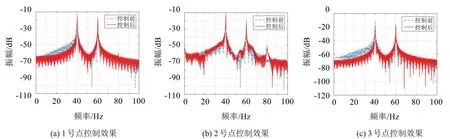
图6 不考虑耦合时对双频激励控制效果

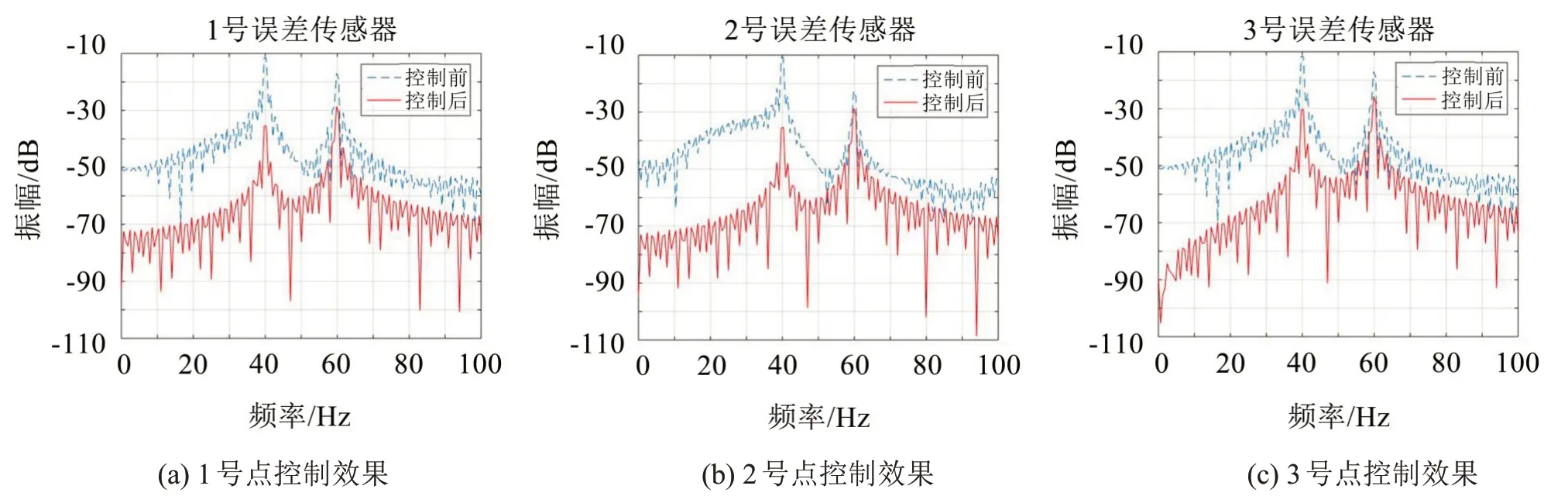
图7 矩阵解耦控制算法对双频激励的控制效果

由图6、图7仿真结果可知，不考虑通道耦合时直接进行控制，3 个控制点处基本处于控制失效状态，甚至出现振动加剧情况；而矩阵解耦优化算法使3个控制点处都产生较好的隔振效果，其平均隔振效果可达24 dB（40 Hz）和11 dB（60 Hz），1号控制点效果最佳。仿真结果表明在多通道控制时矩阵解耦优化是非常有必要的。由于所用激励线谱频率均为100 Hz以下，为了更加直观描述控制效果，频谱图中横坐标频率的范围设为0～100 Hz，控制系统在0～100 Hz振动减小，但超过100 Hz频段则可能表现出频谱变大，并非在全频段均为频谱下降。

3.3 多通道控制试验

搭建控制平台，涉及的主要设备有主被动一体化电磁作动器、激振器、LA-200 功率放大器、dSPACE 控制系统及台架、直流稳压稳流电源及Junus JSP-180-30驱动器、加速度传感器和XK343L-8信号调理器等。平台上安装4个作动器，第4个仅作为被动装置起支撑作用。双层隔振平台及部分设备如图8所示。

图8 试验台架及部分设备

将上层加速度信号作为控制系统的参考输入信号，将中层加速度信号作为控制系统的误差信号。试验中采用37 Hz 与110 Hz 的双频振动激励，采样间隔为0.000 1 s。三通道矩阵解耦控制前后3 个点的频域响应如图9所示。

图9中表明了3 个加速度传感器信号控制前后的频域响应，37 Hz线谱的控制效果优于110 Hz。各频率隔振效果具体情况如表1所示。

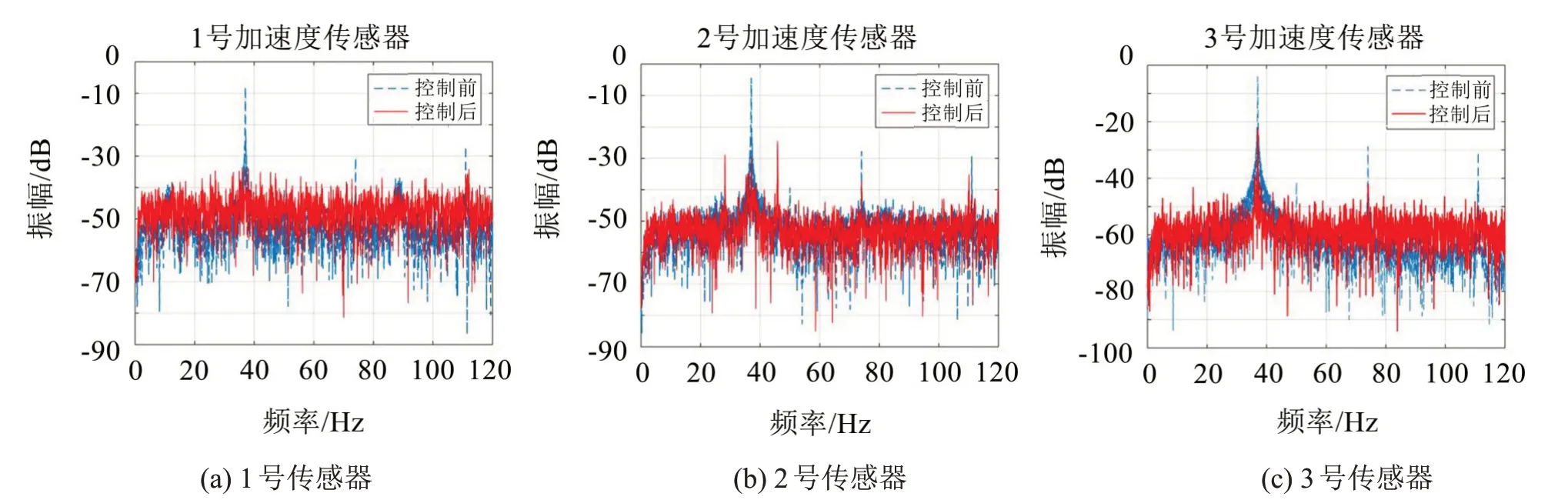
图9 三通道集中式控制效果

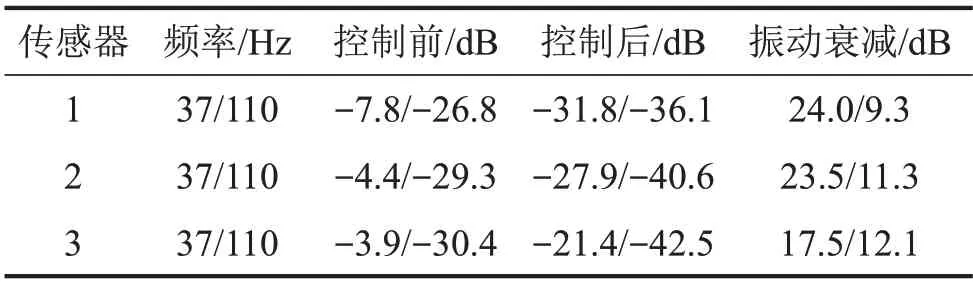
表1 控制前后三通道振动衰减情况

表1中可以直观看出三通道矩阵解耦控制对于双频线谱激励有较好的控制效果，平均振动衰减可达21.6 dB（37 Hz）和10.9 dB（110 Hz），其中在2号控制点的隔振控制效果最佳。

4 结语

本文将矩阵解耦优化算法应用于多自由度主动隔振系统中，并进行仿真和试验分析。针对控制系统中的次级通道耦合，基于前馈补偿原理提出一种矩阵解耦优化算法。为增强作动器与临近传感器之间传递函数的作用，解耦矩阵主对角元素设为1，给出解耦矩阵工程实现方法。解耦后的系统等效为多个单回路系统，提高了算法的稳定性，减小计算量。

搭建双层隔振试验平台进行仿真和试验验证，结果表明：矩阵解耦优化算法对于双频线谱激励有良好的控制效果，3 个点的平均振动衰减为21.6 dB(37 Hz)和10.9 dB(110 Hz)。