金属橡胶材料迟滞特性力学模型研究

邹龙庆，曹义威，付海龙，王 玥

（东北石油大学 机械科学与工程学院，黑龙江 大庆市163000）

金属橡胶阻尼性能好，可塑性强，可在恶劣的环境中保持良好性能，在航天航空、交通运输及工业生产等方面有着广泛的应用前景。金属橡胶材料在加卸载过程中表现出较强的非线性迟滞特性，国内外学者针对该特性进行深入研究，并建立了多种力学模型，最具代表性的有迹法等效阻尼模型、双折线恢复力模型和混合阻尼模型[1-2]等。其中将恢复力分解为弹性恢复力、黏性恢复力和干摩擦恢复力的模型能够很好描述系统出现干摩擦时的情景，该类模型在实际工况中得到广泛应用。在众多模型中，双线性恢复力模型形式简单，参数识别精度较高，实际生产中应用最为广泛。该模型将黏性恢复力和干摩擦恢复力单独表示，虽能够很好地描述恢复机理，但模型中用线性方程表达黏性恢复力和干摩擦恢复力，很多情况下，不能准确体现其非线性特征，特别在材料参数识别应用时，受材料制备参数影响较大。有记忆型恢复力模型基于双折线恢复力模型，将弹性恢复力改为5 次非线性方程，由非线性黏性阻尼力和干摩擦阻尼力构造而成。有记忆恢复模型较之双折线模型在描述高阶非线性材料迟滞特性方面获得较大进步，可用于分析黏性恢复力和干摩擦恢复力所占比例及变化规律[3-4]。

有记忆型恢复力模型将恢复力分解为无记忆弹性力部分和有记忆阻尼力部分，考虑了变形对恢复力的影响，弥补了双线性的不足。但因其干摩擦恢复力部分采用微分形式表达，导致该模型表达式复杂，求解困难。针对此问题本文旨在充分考虑干摩擦恢复力非线性的基础上，利用微元结构理论进一步优化有记忆型恢复力模型，并利用谐振动试验验证。

1 有记忆型恢复力力学模型的优化

1.1 金属橡胶试块恢复力分析

金属橡胶有记忆型恢复力模型中，与整个变形有关的阻尼部分有着复杂的阻尼耗能机理，主要包括两部分，一是部分金属丝之间发生滑移和变形，原有形态及相对位置发生改变，并产生永久变形，该部分表现为黏性阻尼；另一部分为金属丝接触面在受力时发生相对滑动，在摩擦力的作用下所引起的阻尼为干摩擦结构阻尼[5]。以上两种恢复力有着复杂的非线性特性，是恢复力模型中主要研究部分，文中着重对干摩擦恢复力部分进行优化研究。

非线性弹性恢复力采用5 次高阶多项式表示，即

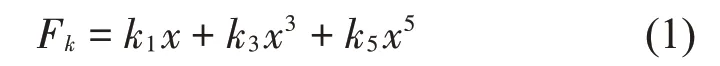
式中：Fk为非线性弹性恢复力；x为金属橡胶加载位移；k1、k3、k5为弹性系数。

对于金属橡胶非线性恢复力，传统上通常采用两种形式表达，即采用等效阻尼力整体表示金属橡胶非线性阻尼力，另一种形式是将非线性阻尼力细化，分为黏性阻尼力和干摩擦阻尼力[6]。为进一步研究干摩擦阻尼力产生机理，本文采用后者，用黏性阻尼力和干摩擦阻尼力之和表示非线性阻尼力。金属橡胶黏性阻尼特性与振幅和振频相关，其中一次黏性阻尼项占主要成分，高次速度项可忽略不计。因此黏性阻尼力部分可表示为

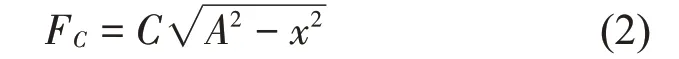
其中：C为黏性阻尼系数，A为振动幅值。

1.2 干摩擦阻尼力

金属橡胶试块是金属丝螺旋卷经过拉伸、缠绕、冲压而成型。在加卸载过程中，随着运动空间的减少，金属丝螺旋卷相互接触并发生相对滑动，产生干摩擦阻尼力。在加卸载过程中，金属丝螺旋卷接触状态不断变化，通过对不同接触状态金属丝螺旋卷进行力学分析，研究干摩擦阻尼力产生机理[7]。结合不同接触状态螺旋卷随位移变化的规律，推导宏观下金属橡胶构件的干摩擦阻尼力。

金属橡胶基本结构单元为金属丝螺旋卷，如图1所示。图中LJ为螺旋卷螺距；DJ为螺旋卷直径；ds为金属丝直径；α为螺旋升角。

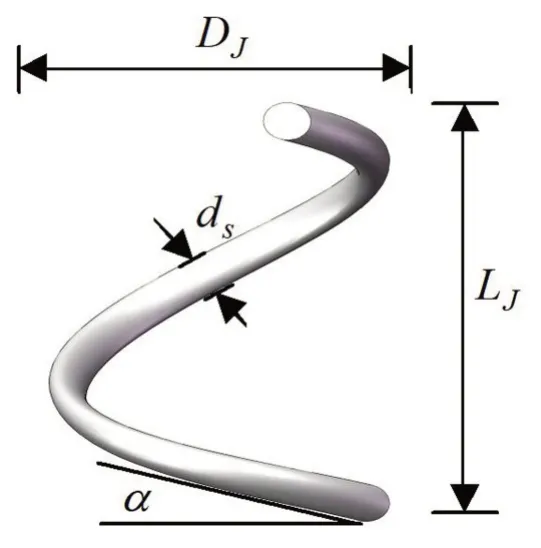
图1 螺旋卷结构图

在加卸载过程中，微元体相互挤压并产生相对滑动，引起内摩擦耗能，是产生干摩擦阻尼力的主要形式。为此干摩擦阻尼力问题可转化为螺旋卷滑移问题。由力学分析可知，在加载过程中，载荷首先克服微元体刚度下移，随着微元体变形不断增大，接触点切向力增大，当切向力大于临界摩擦力时，螺旋卷产生相对滑动；卸载过程中，随着载荷减小，在结构刚度的作用下，微元体恢复原有形状。

如图2所示，支撑力FN由下部横向螺旋卷结构刚度KT提供，KT根据材料和圆柱螺旋压缩弹簧基本理论[8]来确定。

图2 滑移接触加载过程示意图

E为金属丝材料的弹性模量；υ为金属丝材料的泊松比。

加载过程中，随着金属橡胶试块体积不断减小，金属丝螺旋卷接触状态也随之从未接触状态到滑移状态转化，随体积进一步减小，滑移状态微元体转化为挤压状态。微元体状态数目比例与金属橡胶试块相对密度有着复杂的对应关系，假设二者成二次非线性关系，得到如图3所示的变化趋势。

图3 不同接触状态微元体数目比例图

横坐标为金属橡胶试块相对密度，纵坐标n为不同接触状态微元体数目比例。

图中为随位移加载量不断变化的金属橡胶试块相对密度。其中曲线1为未接触状态微元体数目和挤压状态微元体数目比例，在之前为未接触状态微元体比例之后为挤压状态微元体比例。曲线2为随加载位移而不断变化的滑移状态微元体数目的比例。两曲线在相同相对密度下比例系数和为1。其中为采用拉伸编织工艺后及毛坯状态的相对密度，毛坯状态的微元体的接触状态为未接触。根据毛坯结构可得毛坯状态密度

为金属橡胶构件在弹性范围内能达到的最大相对密度，通常情况下其值在0.3～0.4 变化。金属橡胶构件微元体总数目N可根据其成型参数确定

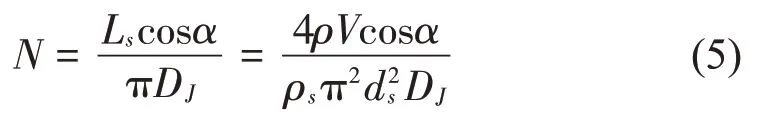
式中：Ls为金属丝长度；ρ为金属橡胶试块密度；V为金属橡胶试块体积；ρs为金属丝密度。

根据相对密度变化确定3种接触状态微元体数目，由于干摩擦耗能只与滑移状态微元体贡献数目相关［9］，得滑移状态的微软体数目比例ns

结合以上公式可得到随位移不断变化的干摩擦力Ff

其中：μ为干摩擦系数。

结合式（1）、式（2）和式（7）得到金属橡胶构件的本构关系

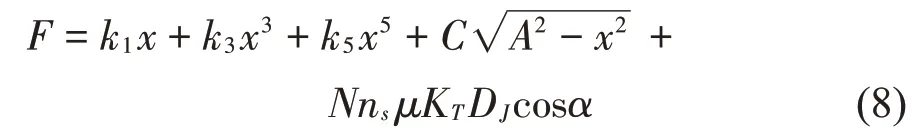
上文干摩擦阻尼力分析中只考虑了一组螺旋卷的相互作用，实际状态下周围螺旋卷对该组螺旋卷产生挤压、摩擦等影响，随着振幅的增大，影响程度随之增加。因此在干摩擦阻尼力部分引入与振动幅值A相关的修正系数B，得到以下数学模型

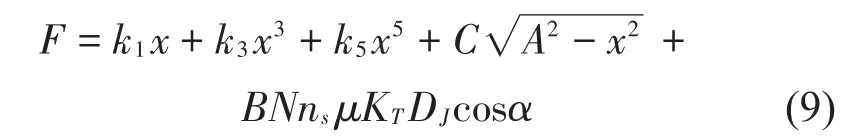
式中干摩擦阻尼修正系数B可由试验获得。

2 金属橡胶准静态试验研究

金属橡胶恢复力在宏观上表现为具有记忆特性的迟滞回线[10]。图4中1为加载曲线，2为卸载曲线。加载时，黏性阻尼力和干摩擦阻尼力阻止内部金属丝的变形，表现为金属橡胶块刚度变大；卸载时，黏性阻尼力和干摩擦阻尼力方向改变，阻止变形恢复，变为金属橡胶实际刚度减小。

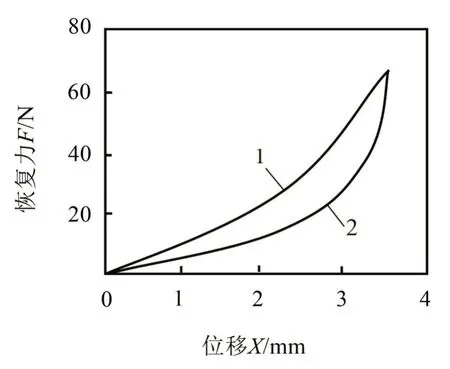
图4 金属橡胶迟滞回线

加载曲线和卸载曲线所围面积代表黏性阻尼力和干摩擦阻尼力在单个振动周期内耗能，体现金属橡胶减振能力。金属橡胶迟滞曲线可由加卸载时力-位移曲线得到。

金属橡胶试块结构参数中，相对密度对金属橡胶迟滞特性有较大影响，为验证优化后有记忆型恢复力模型准确性及适用性，通过试验研究不同相对密度金属橡胶试块的迟滞回线。

2.1 金属橡胶试块的制备

采用直径为0.2 mm、密度为7.93 kg/cm3的奥氏体不锈钢303 金属丝为原材料，利用金属橡胶卷簧机床机制备金属丝螺旋卷，并经等距拉伸至恒定螺距2 mm，通过模具绕制与冲压成型，制备得到高为20 mm、内外径分别为16 mm和36 mm的柱型构件，如图5所示。

图5 金属橡胶试块

保持形状因子β为0.32，制备出2种不同相对密度的试块，详细参数如表1所示。

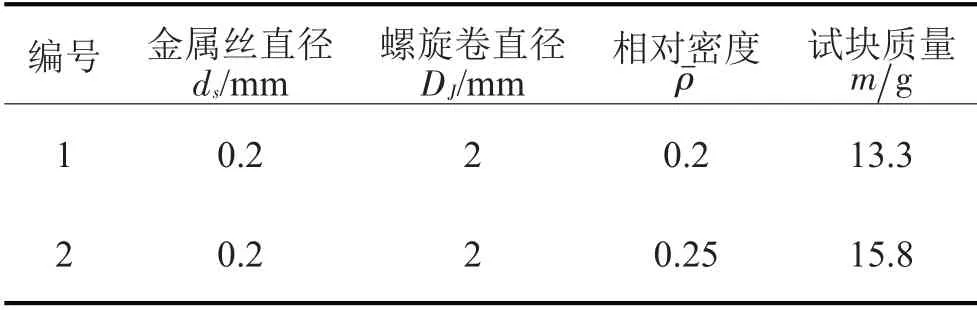
表1 试块基本参数

2.2 理论与试验对比分析

为验证理论模型可靠性和在静态激励下的适用性，采用准静态试验对模型进行验证。试验采用CMT5105型全数字化金属材料电子万能试验机，通过可编程控制器实施加载和卸载，如图6所示。

图6 试验装置及金属橡胶试块安装

分别对2组金属橡胶试块进行准静态加卸载试验，为保证初始载荷与位移的准确性，试验开始前，对试块预加2 mm的压缩位移，试验中控制加卸载速率为5 mm/min，最大加载位移为6 mm。对试验数据进行处理得到如图7所示结果。

为验证数学模型的可靠性，利用试验所得数据对式（9）进行参数识别。优化后的模型无复杂的微分形式，结构较简单，可采用普通的非线性最小二乘法对式中参数进行一次性识别[11]。

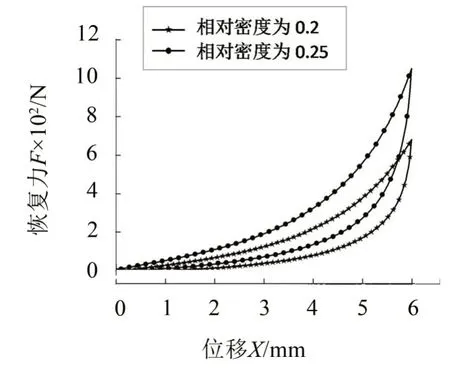
图7 不同相对密度试块加卸载试验

利用相对密度为0.2 和相对密度为0.25 的试块进行理论验证，得到的试验值和理论值如图8所示。

可以看出在不同的相对密度下，该理论模型与试验值都能很好拟合，尤其当相对密度较大时拟合精度更高。虽有误差，但模型一定程度上可以准确描述金属橡胶试块迟滞恢复力特性。误差产生的原因为在用理论模型进行微元体结构力学分析时，根据材料和结构性形式加载刚度设定为定刚度，而在实际的金属橡胶试块内部，螺旋卷刚度不仅随结构变形而改变，并且受周围微元体的影响，刚度表现为较强的非线性。

3 数学模型物理意义辨析

数学模型中参数有明确的物理意义，对于指导工程应用有着重要的作用。为辨析本文建立的金属橡胶迟滞特性本构模型中参数物理意义，选取相对密度为0.2金属橡胶试块进行试验，参数识别中采用加载速度为5 mm/min、加载幅值分别为2 mm、4 mm、6 mm 和8 mm 的试验值。识别结果如表2所示。

表2 加载幅值为2 mm至8 mm的参数识别结果

从表2中识别结果可以看出，非线性弹性恢复力系数随振幅改变呈现出明显规律性，其中低阶刚度系数相对较大，表明在弹性恢复力中低阶刚度系数占主要成分。系数随振幅的增大而减小，表明弹性恢复力在整个恢复力中贡献比例随振幅增大而变小。

该模型中，非线性阻尼力系数也具有明显的物理意义。从识别结果中看出黏性阻尼力系数随着振幅增加而变大，表明黏性阻尼耗能能力随振幅增加而变大，减振特性也会越明显。从表2参数识别结果中可以看出干摩擦阻尼力修正系数B与振幅正相关。如图9所示。

图8 理论值与试验值结果对比

图9 干摩擦阻尼修正系数B和黏性阻尼系数C随加载位移变化曲线

图9中对比黏性阻尼系数C和干摩擦阻尼力修正系数B随振幅变化速率，可看出干摩擦修正系数变化速率较快，表明随着振幅的增加，干摩擦阻尼力贡献比例也在不断增加。

4 结语

（1）从微观角度研究金属橡胶迟滞恢复力特性，通过对金属橡胶螺旋卷结构力学分析及滑移状态微元体数目的变化得出干摩擦阻尼力产生机理：随着位移的增加，金属橡胶螺旋卷接触并发生滑移产生干摩擦，同时滑移接触微元体数目也随位移的增加而增多，增大了干摩擦阻尼力在非线性力中的比重。

（2）提出一种金属橡胶迟滞恢复力模型，该模型考虑了干摩擦阻尼力对迟滞特性的影响，代替原有模型中微分表达形式。优化后的模型中干摩擦阻尼力随位移变化特性清晰且表达形式简练，具有求解简单、适用范围广的优点，弥补了原有微分模型表达式复杂、物理意义不清晰和参数识别过程中求解困难的不足。

（3）提出的金属橡胶迟滞恢复力模型将非线性阻尼力进一步用黏性阻尼力和干摩擦阻尼力准确表示。从参数识别结果可知，非线性弹性力部分1 阶刚度占主要成分，且随着位移的增大刚度减小，说明进入到软特性阶段；非线性阻尼力中，振幅对黏性阻尼力和干摩擦阻尼力都有较大影响，其中干摩擦阻尼力随振幅增加贡献系数不断增大。

本文虽优化了模型表达式，但在描述干摩擦阻尼力时将滑移支撑刚度假设为定刚度，与金属橡胶中复杂的非线性刚度存在差异，与原有微分模型相比降低了计算精度。因此在后续工作中亟待对干摩擦阻尼力分量中的刚度做进一步研究，以提高模型精度。