基于改进的Bertotti 损耗分离模型的铁心损耗计算
李丹丹,朱聪聪,乔振阳,吴宇翔,宋寅卯
(郑州轻工业大学建筑环境工程学院,郑州 450001)
0 引言
电动机、变压器的铁心由磁性材料构成,最常用的磁性材料是硅钢片。电动机、变压器的效率与其损耗密切相关,降低复杂工况下电动机、变压器中的各项损耗对提高其效率有着至关重要的作用[1-2]。因此,精确模拟出硅钢片的损耗特性是优化设计电气设备以及提高产品性能的必要条件。铁心损耗由磁滞损耗、涡流损耗和杂散损耗三部分构成,由于各项损耗产生的机理不同,相应的求解方法和各个因素对于各项损耗的影响程度不同,给精确计算铁心损耗带来了极大的困难[3]。因此,实现铁心损耗的准确分离是精确计算铁心损耗的重要前提。
对于磁性材料损耗特性的研究,目前普遍使用的方法主要分为:①基于实验数据拟合的Steinmetz经验公式法[4];②基于磁化物理机制的磁滞损耗模型法[5];③基于损耗机理的Bertotti损耗分离法[6]。
Steinmetz 公式因计算参数较少,表达形式简单,计算速度较快从而得到了广泛的应用。经典Steinmetz公式只适用于正弦激励下的损耗计算,后续国内外学者对其在非正弦激励情况下的应用展开研究,提出了修正Steinmetz 公式、广义Steinmetz 公式、广义Steinmetz改进公式和Steinmetz 波形系数公式[7-10]。但其缺乏对磁滞现象物理机理的解释,且损耗系数只能通过大量的实验测量数据拟合得到,所以其适用的磁通密度和频率范围较小[11]。且Steinmetz 公式无法实现损耗分离,不能有效地针对各个损耗部分进行分析计算。
磁滞模型主要有Preisach 模型、Jiles-Atherton(JA)模型和Enokizono and Soda(E&S)模型。磁滞模型计算法虽然可以精确地计算出铁心损耗,但是辨识和提取损耗参数依赖于大量的实验数据,辨识过程复杂繁琐且计算量大,不适合实际应用。而且针对不同的模型,参数辨识方法以及损耗参数各不相同,通常每种模型都有特定的测量方法与测量设备,在研究过程中成本较高,也限制了磁滞损耗模型计算方法的推广和应用。
Bertotti从损耗机理出发,将铁心损耗分为磁滞损耗、涡流损耗和杂散损耗三部分,并提出了各个部分的损耗计算公式,实现了损耗分离。针对影响损耗计算精度的各个因素都可以找到相应的损耗部分去修正,大大提高了该模型的适用范围与计算精度。基于损耗分离理论,学者提出了各自改进的铁心损耗计算方法。文献[12]中提出了变磁通密度和变频损耗分离法,但并未考虑磁感应强度和频率对磁性材料损耗的影响。文献[13]中考虑了磁感应强度对磁滞损耗的影响,但并未考虑磁通密度峰值Bm对统计特征参数V0的影响。文献[14]中根据实验数据,采用最小二乘法进行线性拟合,确定了磁滞损耗和涡流损耗的损耗参数,但是忽略了杂散损耗的影响。
本文基于Bertotti损耗分离模型,将磁滞损耗参数表示成与Bm相关的多个部分,并拟合相应的参数。通过分析杂散损耗与频率之间的关系,将斜率k 表示成与频率有关的多项式函数,进而提出了一种改进的损耗模型。使用改进损耗模型对取向硅钢片在不同磁通密度峰值下的损耗特性进行模拟研究,分析对比了模拟结果与实验结果,结果证明改进模型的有效性与准确性。
1 取向硅钢片的磁特性测量
1.1 磁性材料参数
采用宝钢生产的27Q120 型号取向硅钢片作为测量样件,此硅钢片铁损低,磁感应强度高,叠装系数高,容易剪切,切片尺寸精度高,常用于电动机、变压器和互感器等电气设备。取向硅钢片的主要参数:密度7.65 ×103kg/m3,电导率2.27 MS/m,厚度0.27 mm,有效截面积46.7 mm2。
1.2 磁性能测试平台
根据GB/T3655—2008《用爱泼斯坦方圈测量电工钢片(带)磁性能的方法》,选取24 片27Q120 为测试样件,尺寸为30 mm×300 mm,使用TD8510 硅钢片磁性能测试系统对磁性材料进行磁特性测量,得到磁通密度峰值Bm、磁场强度H、铁心损耗P 等磁特性数据,测试平台如图1 所示。

图1 爱泼斯坦方圈和TD8510磁性能测试系统
TD8510 是专用于检测硅钢片交流磁性能的测试系统,具有专用的校准接线端钮,可通过等级的电压表、电流表、功率表对系统进行校准,可在40~1 000 Hz(可选)频率范围内,准确测量晶粒取向型或无取向型硅钢片的交流磁特性参数,并绘制相应的磁特性曲线。TD8510 测试系统的规格参数:磁场强度范围1~10 kA/m,磁感应强度范围0.01~1.9 T,测量频率范围40~200 Hz(可选),测量损耗范围0~350 W/kg,有效励磁功率0~500 VA/kg。
1.3 建立实验数据库
本文分别测量了0.5、0.75、1.0、1.25、1.5 T 时,频率从40~400 Hz的磁性能数据,通过对磁性能数据的处理建立实验数据库。根据所建立的实验数据库分析频率和磁感应强度对磁滞损耗和杂散损耗的影响,同时为损耗参数的确定和损耗分离提供了数据支持。
2 改进的Bertotti损耗分离模型
根据Bertotti损耗分离理论,铁耗分离模型,
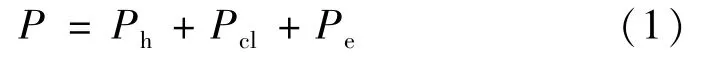
式中:Ph、Pcl和Pe分别为磁滞损耗、涡流损耗和杂散损耗。
为了减少变量的影响,便于损耗分离。将式(1)等价为每个周期损失的能量:
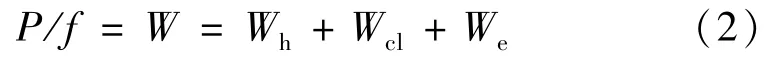
式中:Wh、Wcl和We分别为磁滞损耗能量、涡流损耗能量和杂散损耗能量。
其中涡流损耗是由于磁通随时间交变,磁性材料产生感应电动势而产生的涡流引起的,在本文中涡流损耗由公式计算,故研究时可当常数处理。在计算涡流损耗时,若忽略硅钢片的趋肤效应,正弦激励下涡流损耗能量为

式中:f 为频率;Bm为最大磁感应强度;kcl为涡流损耗系数,

σ为硅钢片电导率,S/m;d为硅钢片厚度,m;ρ为硅钢片密度,kg/m3。
2.1 磁滞损耗
目前普遍使用的损耗计算方法为Bertotti 经典常系数模型,通过式(3)求出正弦激励下的涡流损耗能量后,该模型可表示为磁滞损耗与杂散损耗能量之和,如下式所示[15]:

式中:W为铁心损耗能量;Wh0为Wh+We与f0.5的函数关系为线性时所对应的截距;S 为叠片截面积;G 为无量纲系数(G=0.137 5);V0为表征统计特征参数,其数值大小与Bm有关。为方便下文研究问题,令k=
根据实验测量的取向硅钢片磁性能数据,由式(5)计算出Bm=0.75 T,f=40~400 Hz 时的Wh+We损耗能量分布图,如图2 所示。经大量的实验证明[16-17],当激磁频率为0~15 Hz时,Wh+We的增长速度小于其他频率,在计算损耗时,经典常系数模型往往将Wh+We与f0.5之间的函数关系式当作直线处理(截距为Wh0),忽略了当频率为零时磁滞损耗能量的误差,导致在特定磁通密度下杂散损耗偏大,进而影响铁心损耗的计算精度。
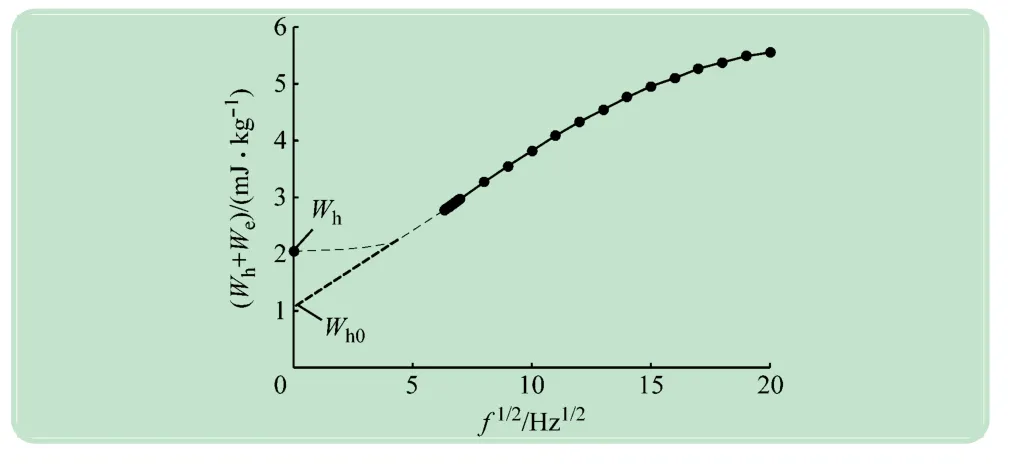
图2 Wh +We 的损耗能量分布
基于Barbisio的研究[16],考虑频率为零时磁滞损耗能量的误差,在Wh+We与f0.5的函数关系式当作直线处理的基础上(截距为Wh0),将磁滞损耗能量误差表示为频率无关项2n0V0Bm,此时,频率为零时磁滞损耗能量即为两者加和,如下式所示,

式中:n0为表征统计特征参数,其数值大小与Bm有关。
此时铁心损耗计算公式为

式中:kh、α为磁滞损耗参数。
因此,为了提高损耗分离的准确性与铁心损耗的计算精度,采用式(7)所示的损耗分离模型进行研究计算。
由式(7)和图2 可知,待提取的参数为磁滞损耗能量、磁滞损耗系数kh、α 和统计特征参数n0、V0。磁滞损耗能量Wh为Wh+We与f1/2之间的函数关系式在频率为零时所对应的截距。大部分学者通常采用直流磁特性测试系统(f=0 Hz)或者由低频(3~20 Hz)损耗数据拟合获得磁滞损耗能量,这两种方法对设备在低频时的测量精度有很高的要求,大大限制了该计算模型的推广与使用。基于此,本文提出了一种确定磁滞损耗能量的方法,该方法首先利用常系数法确定了特定磁通密度下的Wh0;其次联立式(6)与(7),基于特定磁通密度,不同频率下的损耗数据,利用最小二乘法计算得统计特征参数n0、V0;最后利用式(6)计算得出频率为零时的磁滞损耗能量Wh。
硅钢片的磁化具有非线性特性,其损耗与激励频率和磁通密度不是简单的线性关系,若将损耗参数拟合成常数在频率或者磁通密度较高时会产生较大的误差。因此,为了提高改进模型损耗模拟的精确度,将损耗参数α表示为磁通密度峰值的多项式函数,其拟合公式为
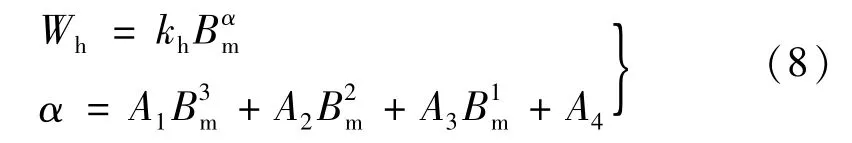
利用上述方法分别计算在磁通密度为0.5、0.75、1.0、1.25、1.5 T时相应的磁滞损耗能量Wh,然后采用非线性最小二乘法确定磁滞损耗参数kh、α。图3 为拟合α 为Bm的多项式后的磁滞损耗能量分布图,从图中可明显看出,该方法的计算精度较高,拟合效果较好。

图3 磁滞损耗能量
2.2 杂散损耗
对于杂散损耗,联立式(7)与(8),基于求得的参数统计特征参数n0、V0,计算出0.75 T 时Wh+We实验值与计算值的损耗能量分布图,如图4 所示。从图4可以看出,当n0、V0为常数且频率高于200 Hz时,计算值与实验值的相对误差逐渐增大,模拟效果有所下降。其原因是函数关系式(式(7))的斜率k 并不是一个常数,实验值的曲线斜率随着频率的增大而减小,若将斜率k和统计特征参数都拟合为常数,则会导致在高频情况下计算值大于实验值。

图4 0.75 T时Wh +We 实验值与计算值
为了使其能在任意频率下准确地计算杂散损耗,将斜率k拟合为频率f的多项式,
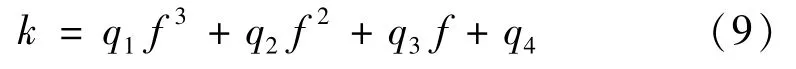
基于上述分析可知,本文首先利用常系数法和最小二乘法确定了不同磁感应强度下的磁滞损耗能量Wh;其次结合式(8)拟合得到磁滞损耗参数;最后在准确计算磁滞损耗能量的基础上,利用不同频率下的杂散损耗能量,结合式(9)拟合得到杂散损耗参数。以磁感应强度为0.75 T 为例,求得的损耗参数如表1所示。

表1 0.75 T时损耗参数
基于上述确定的损耗参数,联立式(7)~(9),计算0.75 T时的Wh+We损耗能量分布图,如图5 所示。
对比图4 和图5 可知,当斜率k 拟合为频率的多项式函数时,无论在高频或者低频的情况下,都有效地降低了k为常数时的误差,提高了计算精度。

图5 0.75 T时Wh +We 实验值与拟合值对比
基于上述分析可知,本文分别对磁滞损耗和杂散损耗的损耗参数进行了修正,确定了改进后的磁滞损耗与杂散损耗的计算公式,即建立了改进的铁心损耗计算模型,以磁感应强度为0.75 T 为例,改进的铁心损耗计算公式:

3 取向硅钢片铁心损耗的计算
为了验证本文所提改进损耗分离模型的准确性,在磁通密度峰值为0.75 T 和1.5 T 时,分别使用Bertotti经典常系数模型与改进损耗分离模型对取向硅钢片27Q120 进行损耗计算,并将计算结果与实验结果进行对比,如图6 所示。
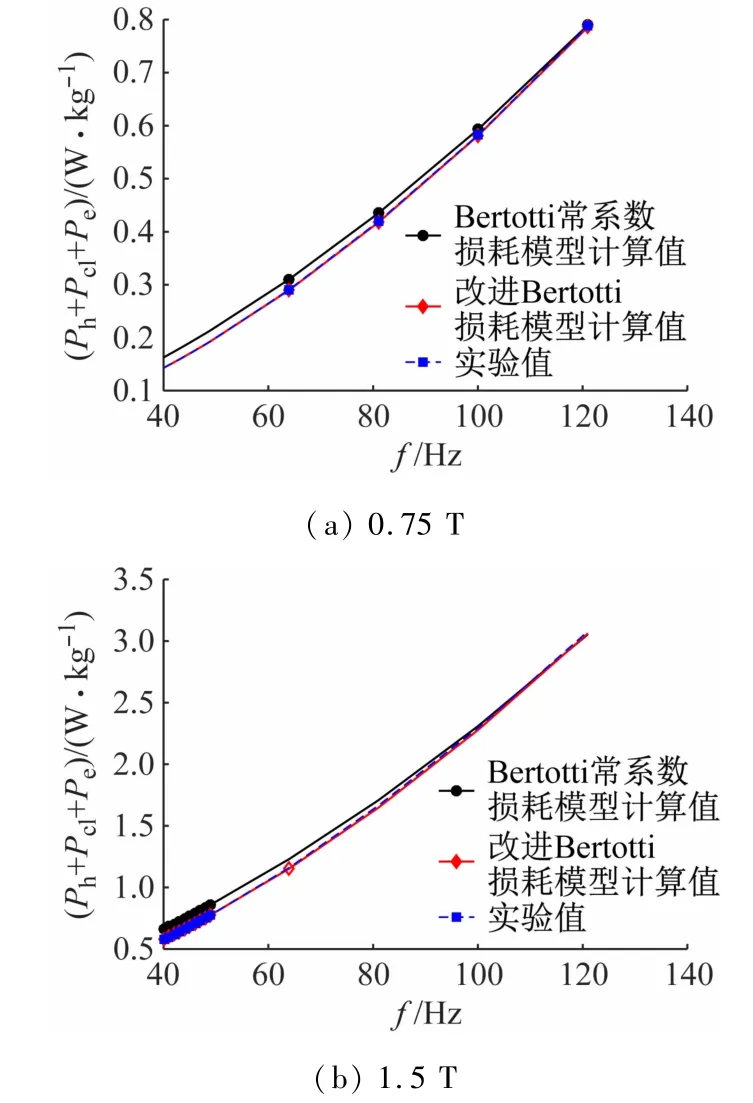
图6 铁心损耗实验值与计算值的对比
由图6 可知,在40~100 Hz 条件下,经典损耗模型拟合效果较差,最大相对误差高达14%。本文所使用的改进模型则拟合效果较好,最大相对误差仅有0.5%。其原因是经典损耗模型忽略了2n0V0Bm的影响,导致杂散损耗计算值大于实验值,且会严重影响损耗占比。磁通密度峰值一定时,随着频率的增大误差逐渐减小。进一步分析损耗与频率之间的关系可知,Bertotti常系数损耗模型的损耗曲线随着频率的增大,逐渐趋近于相同工况下实验值,拟合精度也相应提高。且在不同磁通密度峰值时,其损耗曲线趋近速度各不相同,例如Bm=1.5 T,在频率为100 Hz时损耗误差为0.6%,而Bm=0.5 T,在频率为100 Hz时损耗误差为1.8%。究其原因,是因为随着频率的增大,2n0V0Bm的损耗占比逐渐减小,在达到一定频率时,可近似忽略2n0V0Bm的影响,采用Bertotti 常系数损耗模型进行铁心损耗计算。
为了进一步验证改进模型在不同磁感应强度下的适应性与准确性,本文使用改进的Bertotti损耗分离模型分别对磁通密度峰值为0.5、0.75、1.0、1.25、1.5 T时取向硅钢片的铁心损耗能量进行模拟计算。并将计算结果与实验结果进行对比分析,如图7 所示。

图7 不同磁通密度峰值下损耗能量计算值与实验值对比
从图7 可以看出,在正弦激励下该改进损耗分离模型在磁通密度峰值为0.5~1.5 T时,采用本文所提出的铁心损耗计算方法得到的损耗值与实验值较为接近,拟合效果较好,验证了本文所提方法的准确性。
4 结语
本文基于Bertotti损耗分离模型,综合考虑了磁通密度峰值和频率对磁滞损耗和杂散损耗的影响,对损耗公式进行了更加细化的研究与改进,进而提出了一种改进的损耗模型。该改进模型将磁滞损耗参数拟合为磁感应强度函数,并针对杂散损耗在高频时的误差,将杂散损耗计算式中斜率k 拟合为频率的函数,且考虑了频率无关项2n0V0Bm的影响,进而提高了铁心损耗的计算精度。通过对不同磁通密度峰值下铁心损耗能量的实验结果与计算结果对比分析,验证了改进模型的有效性与实用性。

