走出误区 快速解题

文徐 艳

（作者单位：江苏省南京市竹山中学）

在学习二次函数时，由于同学们对二次函数的定义、图像与性质认识不够深刻，对求二次函数的顶点坐标和对称轴，二次函数解析式，二次函数的根与系数的关系，二次函数与方程（组）、不等式的关系等掌握不牢固，解题方法选择不当，被题中的干扰项迷惑，常常会出现一些典型的错误。本文选取几例典型错解加以剖析，希望能帮助同学们走出思维误区，快速准确地解决问题。

易错点1：对二次函数概念的理解模糊不清

例1 若y=（m2+3m+2）xm2+m为二次函数，则m的值为（ ）。

A.-2或1 B.-2 C.-1 D.1

【错选】A。

【错因分析】由二次函数y=ax2+bx+c（a，b，c是常数，a≠0）的定义可知m2+m=2，且m2+3m+2≠0，解出符合题意的m的值即可。

【解答】由二次函数的定义可得m2+m=2，且 m2+3m+2≠0，解得 m1=1，m2=-2，且m≠-1或-2。∴m=1。

故答案为D。

易错点2：对二次函数图像与性质认识不深

例2 抛物线y=-x2+bx（b≠0）与坐标轴的交点个数为（ ）。

A.0 B.1 C.2 D.3

【错选】D。

【错因分析】先根据b2-4ac＞0判断出抛物线与x轴必有两交点，再根据抛物线必与y轴有一个交点（因为x可以取0），所以错选D。而本题抛物线与y轴的交点是（0，0），与其中一个x轴交点重合。

【解答】当x=0时，y=-x2+bx=0，则抛物线与y轴的交点坐标为（0，0），

∵b2-4ac＞0，

∴抛物线与x轴有两交点，

∴抛物线与坐标轴有两个交点。

故选：C。

【点评】可先计算自变量为0时对应的函数值，得到抛物线与y轴的交点坐标，看是否为原点，再根据b2-4ac判断抛物线与x轴的交点个数，从而更快更准确地得到结果。

易错点3：二次函数系数a，b，c与图像的关系理不清

例3抛物线y=ax2+bx+c的顶点为D（-1，2），与x轴的一个交点A在点（-3，0）和（-2，0）之间，其部分图像如图1，则有以下结论：①b2-4ac＜0；②当x＞-1时，y随x增大而减小；③a+b+c＜0；④若方程ax2+bx+c-m=0没有实数根，则m＞2；⑤3a+c＜0。其中正确结论的个数是（ ）。

图1

A.2 B.3 C.4个 D.5个

【错选】无法判断每一个结论的正误。

【错因分析】①易由抛物线方程与x轴交点个数对应方程根的个数，得到有两个交点对应b2-4ac＞0；②对于对称轴为直线x=-1的情况大家很熟悉，这里只需对照图像，根据二次函数的单调性以对称轴为分界线，在右侧递减；③a+b+c即为x=1时的函数值，结合图像易判断；④容易只考虑用根的判别式b2-4ac＜0来求解m的取值范围，列出不等式后含有太多字母无法求得结果；⑤对a，b，c与函数图像的关系理解不够熟练，找不到突破口，无法将3a与b联系起来。

【解答】（1）∵抛物线顶点（-1，2）在x轴上方，开口向下，

∴抛物线与x轴有两个交点，

∴b2-4ac＞0，故①错误；

（2）∵抛物线开口向下，对称轴为直线x=-1，

∴当x＞-1时，y随x的增大而减小，故②正确；

（3）∵抛物线的对称轴为x=-1，

∴x=1时的函数值和x=-3时的函数值相等，

∴由图可知，a+b+c＜0，故③正确；

（4）∵若方程ax2+bx+c-m=0没有实数根，

∴抛物线y=ax2+bx+c与直线y=m没有交点，

又∵抛物线y=ax2+bx+c开口向下，顶点坐标为（-1，2），

∴m＞2，故④正确；

∴b=2a，

又∵a+b+c＜0，

∴3a+c＜0，故⑤正确。

综上所述，正确的结论有4个。故答案为：C。

易错点4：综合题中对探究性问题的答案考虑不全

例4 如图2，已知二次函数y=x2+bx+c的图像与x轴交于点A（1，0）、B（3，0），与y轴交于点C.

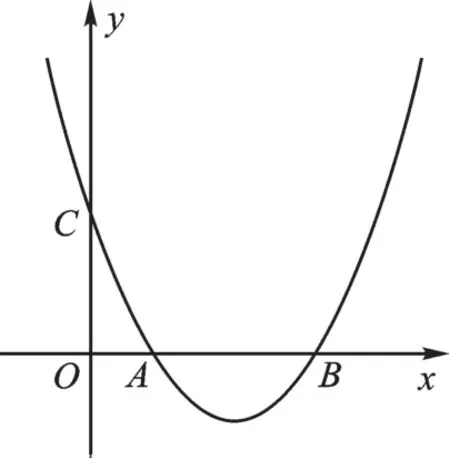
图2

（1）求二次函数的解析式；

（2）若点P为抛物线上的一点，点F为对称轴上的一点，且以点A、B、P、F为顶点的四边形为平行四边形，求点P的坐标。

【错解】一些同学因分类考虑不全对第（2）问造成漏解。

【错因分析】第（2）问在解答时对如何分类掌握得不好，我们只要抓住AB为平行四边形的一条边或平行四边形的对角线两种情况分别求解即可。

【解答】（1）用待定系数法易得二次函数表达式为：y=x2-4x+3。

（2）①当AB为平行四边形一条边时，如图3，

则AB=PF=2，则点P坐标为（4，3），

当点P在对称轴左侧时，即点C的位置，以点A、B、P、F为顶点的四边形为平行四边形，故：点P为（4，3）或（0，3）；

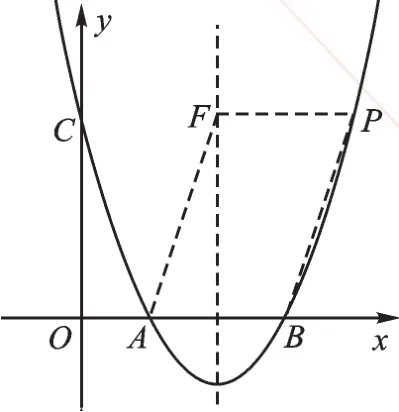
图3

②当AB是四边形的对角线时，如图4，AB中点坐标为（2，0）。

图4

综上所述，点P坐标为（4，3）或（0，3）或（2，-1）。