旋转弹锥形运动气动特性研究*

庞川博,康 顺,赵 超,蒋胜矩,党明利

(1 西安现代控制技术研究所, 西安 710065； 2 西安飞行自动控制研究所, 西安 710065)

0 引言

弹箭旋转飞行具有提高稳定性、消除推力偏心和质量偏心等优点,并且其控制系统更加简化[1]。在旋转过程中,弹体周围流场相对其合攻角平面不对称,在合攻角平面垂直方向上将产生额外马格努斯力与力矩[2](也称面外力与面外力矩)。马格努斯效应除了引入偏航方向上的气动干扰外,还会诱发旋进与章动现象,在上述运动耦合作用下,可能导致弹箭发生马格努斯不稳定而失稳。国内外火箭弹飞行试验中多次出现因马格努斯不稳定而失败的例子,因此旋转弹箭的气动特性也成为国内外学者、工程技术人员研究的焦点。准确预测弹体旋转绕流场的特性，了解其流动机理成为了旋转弹箭气动外形设计、控制系统设计的必然需求。

目前旋转弹箭气动特性的分析手段可分为风洞试验、飞行试验与非定常数值计算。由Dupuis和Hathaway[3]开展的一系列自由飞试验取得了较好的效果,但试验中难以获取流场的细节,无法进一步对旋转运动中产生的流动现象进行分析,且试验还具有成本高、周期长等缺点。随着计算机硬件的发展,非定常数值方法应用于动态过程模拟成为可能,近年来国内外围绕旋转弹气动特性已开展大量工作,其中2007年DeSpirio[4]采用CFD++对M910旋转弹丸绕流场进行数值模拟,结果表明在亚跨音速条件下RANS/LES混合方法能取得与试验值符合较好的结果；2012年Vishal[5]采用CFD++中k-ε湍流模型开展了非定常数值计算,计算结果除轴向力偏高外,其余气动力与动导数都与实验结果符合较好。在国内,薛帮猛[6]等通过对SOCBT弹丸旋转开展数值研究,发现尾部形状对马格努斯力有较大影响,且马格努斯力矩与转速呈线性关系。雷娟棉[7]等通过滑移网格技术计算了高速弹丸的绕流场,发现船尾处边界层增厚,在船尾处产生的压力差主要构成了马格努斯力。肖中云[8]等通过非定常数值计算重点比较了标准形状和船尾形状两种布局的马格努斯力和力矩的变化可以归结为亚声速的绕拐角流动和超声速的膨胀加速流动对尾部边界层位移厚度的影响。在2017年石磊[9-10]等对有翼导弹高速旋转绕流场进行数值模拟,发现大攻角时舵面马格努斯力占较大比重,同时也针对不同湍流模型对带翼旋转弹箭开展了计算,结果表明S-A与SST模型都能较好模拟马格努斯效应。目前国内外大多研究仅围绕弹体自转展开,对弹体旋转引起的章动、锥动等现象进行数值计算分析的工作还较少,文中在建立描述弹箭多轴角运动方法的基础上,采用非定常N-S方法结合RANS湍流模型,对标模Basic finner锥动过程开展动态数值模拟,对旋转过程中流动现象进行分析。

1 数值模拟方法

1.1 控制方程

(1)

式中：Ω为控制体,∂Ω为控制体微元面积,n为积分面的单位法向矢量；Q为守恒形式的状态变量,F(Q)为对流项通量,G(Q)为粘性项通量。在流动未出现较大分离时,非定常RANS方法依然适用于求解旋转弹箭绕流流场[11],故文中采用Menterk-ωSST湍流模型,其具体构造与特性见文献[12]。

1.2 多轴旋转运动的数学描述

根据杨树兴[13]等人总结的旋转弹箭理想情况下,由初始扰动和陀螺效应引起的二圆运动的复攻角方程,将其成复攻角形式并引入陀螺稳定因子后,得到表达式：

(2)

Δ=C1er1t+C2er2t

(3)

式中r1与r2为特征根,具体写为：

(4)

利用欧拉公式,式(2)可在α-β平面内写成随时间变化的迹线形式,考虑到C1与C2是由初始条件决定的待定常数,将初始条件和运动过程写成α-β投影平面内幅值与相位关联的形式,即

Cj=Kjeiφj 0，erjt=e-iφ′jt(j=1,2)

(5)

式(2)最终写作

Δ=K1eiφ1+K2eiφ2

(6)

由式(6)可以看出,在复平面内,通解由两个线性无关的不同幅值、不同频率的圆运动组合而成,依照频率的高低,分别称之为快圆运动与慢圆运动。考虑弹体自转时,二圆运动实际上为弹箭绕3个不同转轴旋转的复合角运动。选取合适的参考系对不同角运动进行描述,再通过坐标变换,即可获得多轴角运动的描述形式。

在相应参考系内,定义沿周向旋进过程扫过的角度为进动角,沿径向臂长变化的角度为章动角,上述两个角度及其微分形式即可对单个圆运动进行完整描述。描述二圆运动所需角度参数包括自转角φ0(对应自转运动)、快圆进动角φf与快圆章动角Kf(对应快圆运动)、慢圆进动角φs与慢圆章动角Ks(对应慢圆运动),下面建立相应参考系对各个角运动进行定义。

图1 惯性坐标系以及初始弹体姿态时尾翼编号

弹体系与惯性系是弹道中常用参考系,其中弹体系与弹体固连,惯性系与地面固连。令惯性系xo方向与来流方向保持一致,且初始时刻弹体轴线处于惯性系xoy平面内(见图 1(a)),此时对4片尾翼进行编号(见图 1(b))。建立与弹轴固连但不跟随其旋转的准弹体系,得到用于描述弹体自转的自转角φ0；将准弹体系绕z轴旋转Kf后得到快圆坐标系,在此基础上类似建立准快圆坐标系,得到用于描述快圆旋进运动的进动角φf；将准快圆坐标系绕z轴旋转Ks后得到慢圆坐标系,同理得到在准慢圆坐标系中用于描述慢圆旋进运动的进动角φs。易知最终的准慢圆坐标系与惯性系是重合的。

注意上述各角度均在各自其给定的参考系下进行描述,目的是使其物理意义更清晰。将自转运动、慢圆运动、快圆运动在各自最初定义的坐标系中分别进行坐标转换(其中自转运动需将坐标系旋转4次,快圆运动需将坐标系旋转2次,慢圆运动旋转0次),最终可写出惯性系下复合角运动各分量的表达式：

(7)

其中：

式中：φf0与φs0为快圆运动与慢圆运动在初始时刻所处姿态角,当其为零时弹体轴线位于惯性系xoy平面内且弹尾位于y+方向；w0、ws与wf分别为自转角速度、慢圆运动和快圆运动的旋进角速度。式(7)具有较好的普遍性,适用于描述定点三轴及以下多轴角运动的姿态及运动过程。

在进行数值计算时,将角运动分量投影至不同时刻弹体坐标系中往往更有实际意义。首先引入角运动的瞬轴概念,其物理意义为：刚体绕某一矢量进行角运动时,若该矢量方向决定了刚体转动的方向,该矢量大小决定了刚体转动的角度,则定义该矢量为当前时刻刚体转动的瞬轴。瞬轴与角位移满足关系：单位时间角位移=瞬轴×单位时间。

容易知道惯性系下瞬轴可写为：

(8)

式(8)为了形式简洁,只将角速度写成时间相关变量。上标I表示该变量在惯性系下进行描述,B1为t1时刻的弹体系。根据上文中已得到的式(7),目前可以写出在惯性系下每个时刻的瞬轴。当弹体旋转时,物面及空间网格一同跟随旋转,旋转后得到新的参考系,称为当地随体坐标系。

在初始时刻,惯性系与当地随体坐标系重合,此时瞬轴在两个坐标系中表达式相同,即

sB1(t)=sI(t)

(9)

下一时刻,网格将绕瞬轴进行第一次旋转,由于瞬轴已知、单位时间步长已知,可构造第一个旋转矩阵,记为R(t1)。旋转矩阵通过矩阵运算将目前坐标系(旧时刻的当地随体系,在初始时刻与惯性系重合)旋转至新坐标系(下一时刻的当地随体系)。

容易得到下一时刻瞬轴在本时刻当地随体系中表达式

sB2(t2)=R-1(t1)·sB1(t2)=R-1(t1)·sI(t2)

(10)

以此类推,再下一时刻

(11)

最终可以写出惯性系下瞬轴旋转至任意时刻当前体轴系下的表达式:

(12)

此时便将刚体的旋转运动方程写成了离散的、投影在当前时刻当地随体参考系中的表达形式,适用于非定常动态数值计算中运动过程的描述。

1.3 计算模型

计算模型采用Basic Finner导弹标模,基本外形为十字布局的带翼导弹,由弹头锥段、圆柱段与尾翼组成,质心位于距弹头55%处,基本几何尺寸见图 2。该标模为美国空军在二战后为开展无控带翼导弹空气动力学和飞行力学特性研究而设计的模型,目前已经过大量的静态与动态气动试验研究,有丰富的静态和动态试验及计算数据。

图2 Basic Finner基本外形尺寸

1.4 数值方法验证

共采用3套疏密不同的网格用于考察数值方法的计算准确性,分别为1)粗网格：网格总量大约400万,边界层底层高度为5×10-6m；2)中等网格：网格总量大约600万,边界层底层高度为2×10-6m；3)较密网格：网格总量大约800万,边界层底层高度为2×10-6m。计算网格采用多块对接的混合网格,弹身表面、近壁面周围以及尾迹区域采用加密后的六面体网格以保证流动特征的捕捉,远场区域采用四面体网格以节省计算资源。计算网格如图 3所示。

图3 计算网格示意图

计算马赫数取1.254,不同网格计算结果均与试验值[14]进行对比。结果如表1所示,表中第一行从左到右分别为：零攻角条件下法向力系数斜率、轴向力系数、相对质心的俯仰力矩系数对攻角的斜率以及滚转力矩系数。所有计算均收敛较好,加密网格后,中等规模网格计算值与试验值已非常接近,可认为中等规模网格已满足需求。

表1 不同疏密网格计算结果对比

2 计算结果与讨论

2.1 计算工况说明

由式(7)可知,当Kf与φ′f为零时,二圆运动退化表现为锥形运动,此时慢圆运动转轴为锥动轴,慢圆运动的章动角为锥动角,慢圆运动的进动角速度即为锥形运动的旋进角速度；文中主要计算状态为锥动角Ks=10°,不同自转角速度与进动角速度下弹体的锥形运动,具体见表2。

表2 不同工况弹体运动参数

工况1、2、3的进动角速度方向和尾翼斜置产生的滚转力矩方向一致；工况1、2弹体无自转,此时运动方式为似月运动,弹体表面迎风区域与背风区域保持不变,相对来流的姿态也不变。工况3中弹体绕自身弹轴旋转,自转角速度是进动角速度的两倍,此时弹体相对来流的姿态在“十”和“X”之间不断变化。非定常时间步长Δt=3.87×10-5s,进动一周的周期T=0.013 9 s,非定常时间推进360步。自由来流状态为：马赫数Ma=1.254,雷诺数Re=8.76×106,温度Tref=288.15 K。

为方便说明,后文将基于惯性系与随体风轴系进行分析,两个坐标系定义如图4。

图4中左图为来流与弹体初始姿态关系,右图为两个坐标系的相对关系。原点o位于弹体质心处,z轴满足右手定则,xoy不随弹体运动而改变,来流与ox方向平行；弹轴与ox夹角为合攻角,由慢圆运动章动角和快圆运动章动角组成(上文中已规定其在初始时刻位置)。弹体作锥形运动旋进时,设坐标系xbybzb跟随弹体进动而旋转(并不跟随自转而旋转),且obxb与ox始终重合。

图4 惯性系xoy与随体风轴系xbybzb示意

2.2 弹箭似月运动气动特性讨论

在上文给出的惯性系下将弹体受力分别沿oy方向和oz方向进行分解,得到的Cy与Cz随进动角变化的曲线如图 5所示。可以看出弹体在不同位置受力满足正弦变化规律,不同的周期之间结果也保持良好一致,且两个工况计算结果相差较小。

图5 惯性系下Cy与Cz随不同相位角变化

分别取上述两个工况非定常计算的最后一个周期,与不同相位下的定常结果以及对非定常结果进行拟合的曲线进行比较,两个工况有类似的结果,故此处仅以工况2为例,给出曲线变化如图 6所示。拟合曲线与非定常计算结果符合较好,可用于描述非定常曲线的相位；与定常结果相比,动态过程受力最大值更大,且具有相位提前的特点,即在进动过程中,在进动角尚未达到179°时(尾翼斜置的影响),Cy已达到正向最大值,Cz同理。通过对比拟合曲线和定常曲线可以得到相位提前的角度,工况1的法向分量Cy的相位提前角大约为5.296°,侧向分量Cz的相位提前角大约为5.094°；工况2的法向分量Cy的相位提前角大约为6.724°,侧向分量Cz的相位提前角大约为6.68°。

相位提前现象与给定的进动角速度有关,下面在随体风轴系下进行讨论,其中Cyb为合攻角平面内的法向分量,Czb为垂直于合攻角平面的侧向分量。弹体绕过质心的锥动轴(即慢圆进动轴)转动构成了一个旋转系统,在不对称斜置尾翼的作用下,该旋转系统在当前马赫数下具有固定的平衡转速,当进动角速度等于当前旋转系统的平衡转速时,滚转力矩Mxb为零,即Czb与Cyb在滚转方向产生的力矩相互抵消,已知Cyb主要由来流在合攻角方向产生,其数值远大于Czb,可认为此时Czb对合力方向影响很小,几乎不发生相位提前效应；当进动角速度大于当前旋转系统平衡转速时,由于滚转力矩Mxb不等于零,弹体Czb必然不为零,此时Czb与Cyb在当前位置合力的方向与之后某时刻所处相位的法向力方向一致,故出现相位提前的特征(见图 7所示)。进动角速度越大,相应的面外力也越大,相位提前效应就越明显,非定常计算结果合力的最大值也越大(合力由合攻角平面内的Cyb与面外力Czb所合成)。

图6 Cy与Cx相对定常解的相位提前量

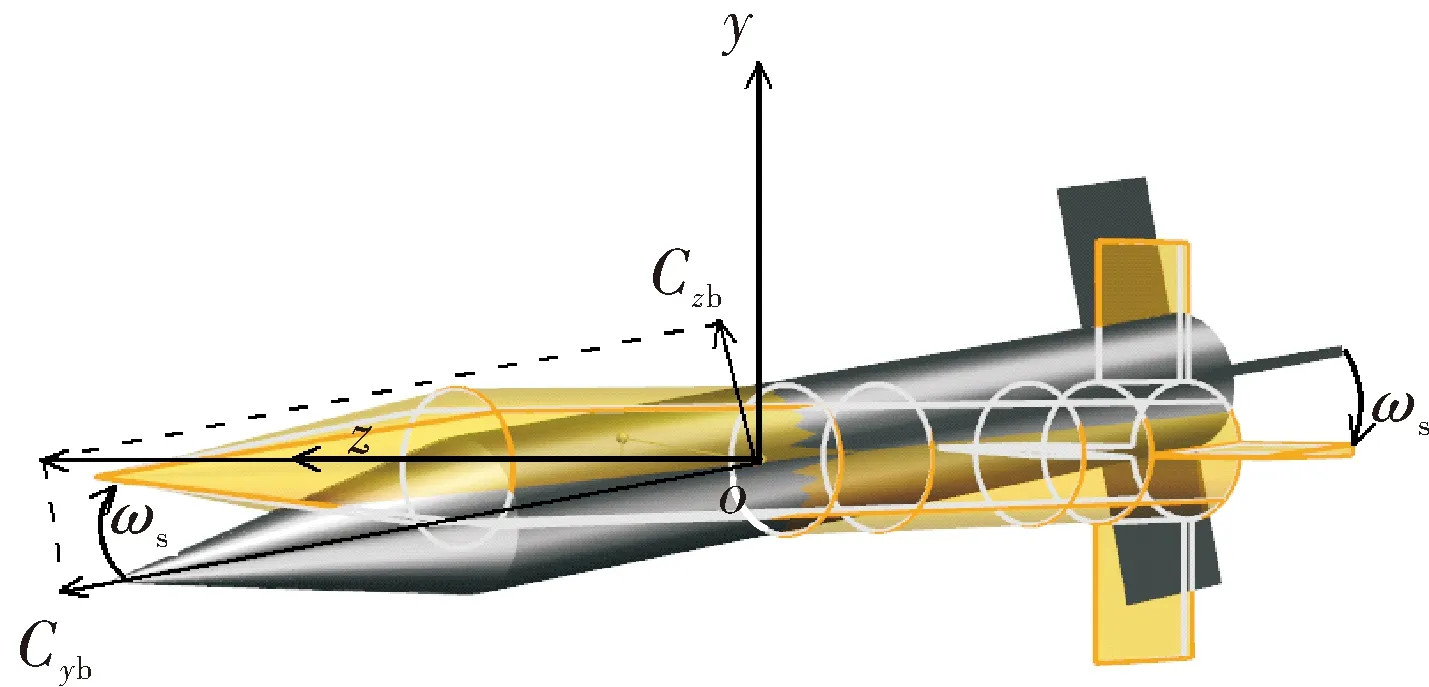
图7 似月运动引起的相位提前现象

从上文中可知,Cy与Cz曲线的相位提前角并不完全相同,两条曲线仍具有一定相位差,Cyb与Czb将呈小幅振荡趋势(若Cy与Cz始终同相位,则Cyb与Czb为固定常值)。将两工况非定常解投影至随体风轴系下,得到如图 8所示结果,分析图中结果得到以下结论：在当前所采用的网格分布和湍流模型的条件下,弹体沿随体风轴系分解得的法向力Cyb和侧向力Czb均随进动角变化产生小幅振荡,进动每经过90°相位,Cyb与Czb完成一个振荡周期；进动角速度变化对Cyb与Czb周期和振幅影响较小,但对Czb的均值有一定影响,当进动角速度大于旋转系统平衡转速时,Czb均值随进动角速度增大而增大。

在图9观察工况2在相位角为零时尾翼1、3流场分布,由于尾翼斜置的原因,尾翼1的进动背风面同时也是自由来流相对尾翼斜置方向的迎风面,尾翼3的进动背风面则是来流相对斜置方向的背风面,且尾翼1翼梢处线速度更大,在来流与旋转综合作用下,尾翼1背风区域能观测到流动分离现象,产生的涡附着于翼梢进动方向背风面,来流的影响使得越接近后缘,涡规模发展越大,分离趋势更加明显,而尾翼3翼梢处并没有明显的分离现象。尾翼1、3的受力变化很大程度上决定了Cyb与Czb的变化趋势,但由于振荡幅值和涡的尺寸均很小,进一步观测和分析涡发展和脱落需要更精细的网格及采用LES方法。

图8 随体风轴系下受力结果

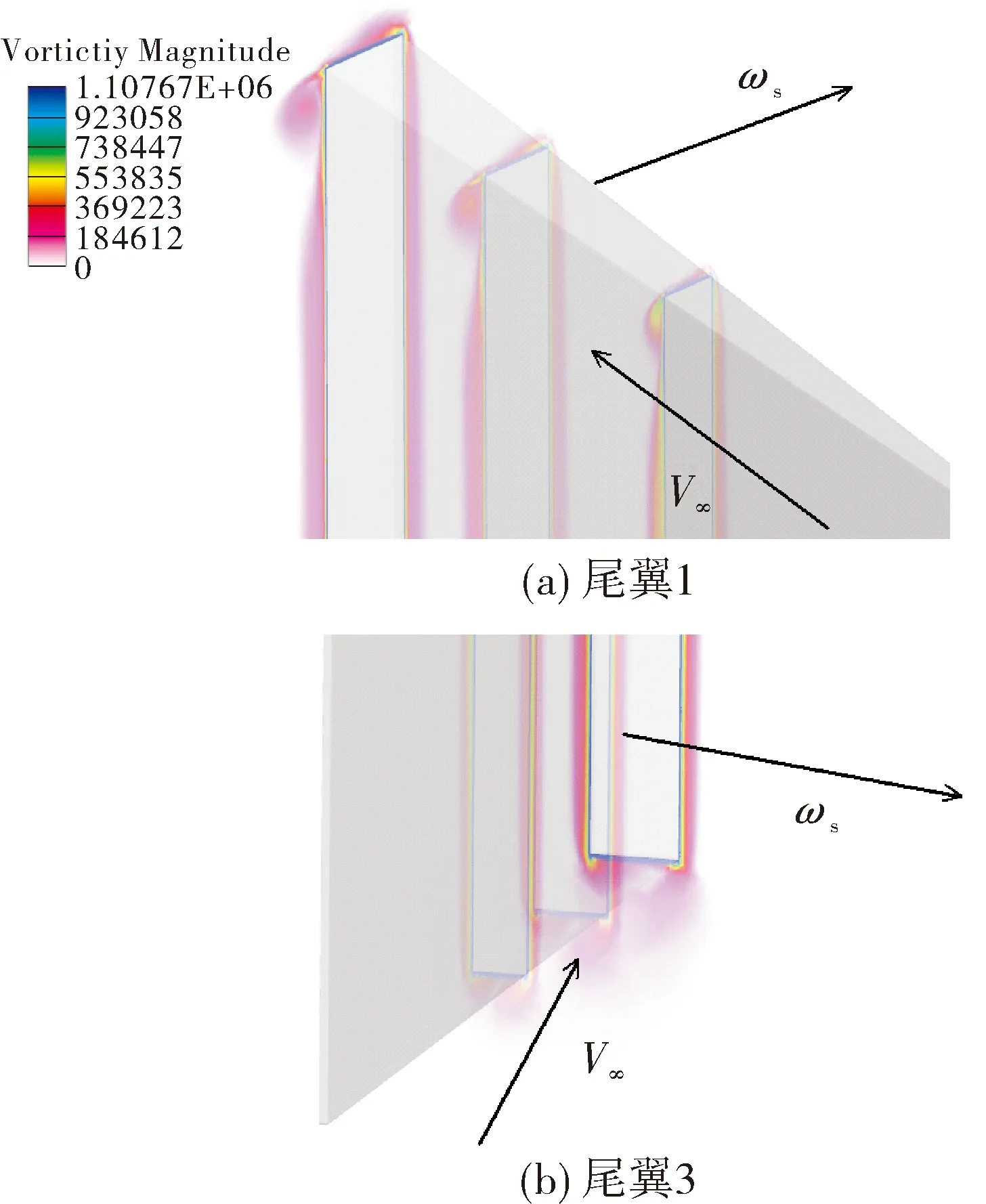
图9 零相位时尾翼附近流场涡量图

2.3 锥形运动中自转的影响

工况3考虑自转角速度,弹体旋进过程中自身相对姿态也在不断变化,取弹体底部过弹轴一点与翼梢处某固定点作为观察点,弹体进动一个周期的观察点轨迹如图 10所示(为方便观察,示意图中旋转中心设在弹头,实际计算时弹体旋转中心在质心处),红色虚线为进动过程的轨迹,而蓝色虚线则为弹体绕弹轴自转的轨迹,在一个进动周期内弹体自转两圈。图 11为工况3与工况2全弹在惯性系下受力分量随进动角变化曲线,通过对比,工况3曲线仍具有一定的正弦变化特征,但与似月运动结果已有较大差别：1)相位略有提前；2)在曲线的波峰与波谷处,即相位角90°、180°与270°处,工况3与工况2的姿态完全相同,但受力分量明显较小；3)曲线整体光顺性较差。

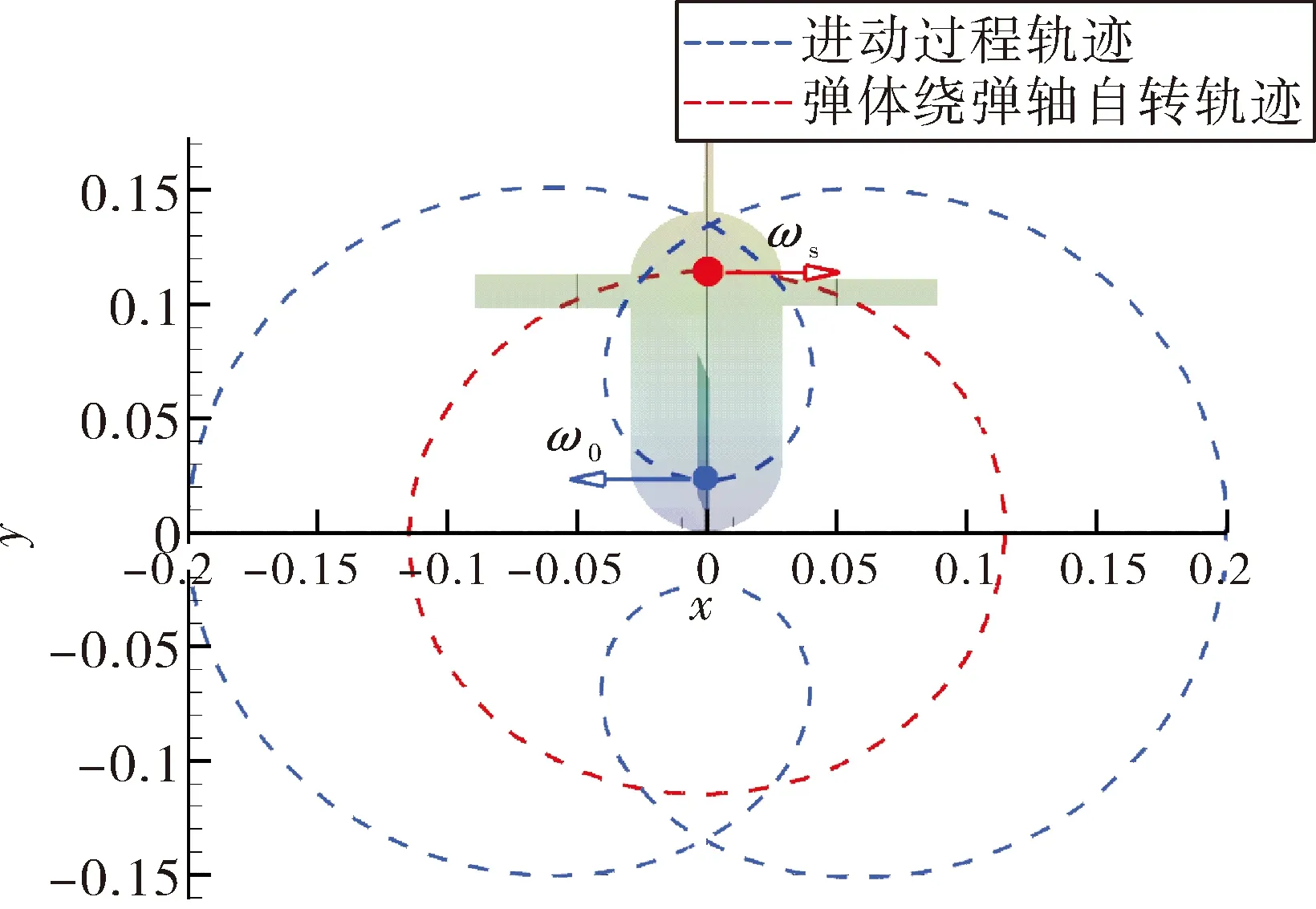
图10 弹体旋进一周期尾部与翼梢观察点轨迹

图11 工况2、3在惯性系下受力曲线

在随体风轴系下进一步分析,首先给出工况3与工况2的受力曲线如图 12所示。对比可知,弹体绕弹轴自转后,其合攻角平面内Cyb与合攻角平面外Czb的均值、振幅、周期均有较大改变。对于工况3,每进动180°,曲线经过一个大周期,每个大周期内有4个小周期,每个小周期对应弹体自转90°；工况3中受力曲线振幅远大于工况2的似月运动,说明弹体自转诱发的翼梢处涡脱落现象更加显著,翼梢处的流动分离也将引起合攻角方向上升力的损失,因旋转引起的平均升力损失大约占总升力的4.55%；两种工况侧向力Czb的变化主要由弹体自转产生的马格努斯效应造成,在有翼弹箭翼体干扰和弹体进动过程与气流的相对作用综合影响下,侧向力Czb均值明显增大,增量占全弹法向力的6.5%左右。Cyb与Czb合力的变化与振幅的不规则改变可以看作是马格努斯效应影响的结果。

图12 随体风轴系下工况2与工况3受力曲线

图13给出进动90°(即1/4周期)时不同截面的涡量分布。两种工况弹身背风区均出现明显流动分离现象；在弹身圆柱段,似月运动使背风区下侧分离涡受到挤压更贴近壁面,而上侧则受相对似月运动的等效来流影响,分离涡远离弹体壁面。工况3结果见图 13(b),弹体旋转引起的环流在弹体上侧与来流分量相反,二者相互阻碍使分离涡更远离弹体且更容易脱落；弹体下侧环流与来流方向相同,使边界层局部速度梯度更大。

图13 t=1/4T时刻不同截面涡量分布

在x=0.54L截面作工况3的压力分布云图,同时给出工况2、3在该相位下弹身截面处的流向压力分布曲线,如图 14所示。从图中可知,由于弹体的进动,两个工况弹身下侧压力均大于上侧压力,同时在背风面处都表现出了明显的上下不对称现象,最高压力点从270°处偏移至255°处；工况3中由于弹身的自转影响,背风区压力分布不对称性更加明显,且普遍在180°相位至270°相位压力更大,弹身旋转所产生的实际面外力指向图中40°相位方向处,符合理论上旋转弹弹身产生马格努斯力方向的规律。靠近弹尾处流动分离与不对称性更加显著,由于弹翼的遮挡作用,背风面漩涡强度降低,涡的形状分布特点与弹身类似。翼梢涡的规模取决于当地垂直翼面气流的相对速度,在尾翼中部靠中后缘区域受激波干扰,边界层增厚,流动更易分离(见图 15)。

图14 x=0.54L压力分布云图与曲线图

图15 尾翼不同截面马赫数分布

3 结论

文中针对旋转诱发的复杂角运动现象,建立适用于计算流体力学的多轴角运动表达形式,对标模Basic Finner的似月运动以及锥形运动开展数值计算,从流场结构和气动载荷变化进行了研究,通过分析得出以下结论：

1)弹箭作似月运动时,沿惯性系各方向受力随相位角变化的曲线,相比定常结果具有相位提前的特征,且进动角速度越大,相位提前量越大。

2)锥动过程中尾翼翼梢及弹尾处存在小尺度流动分离,使得弹体在合攻角平面内与平面外受力呈振荡现象；弹体自转速度为零时侧向力振荡幅值较小,当自转速度不为零时,侧向力均值与振荡幅值显著增大。进一步准确观测和分析该现象需要更精细的网格与更适合的湍流模型。

3)弹体自转会使得弹身背风面以及尾翼翼梢处不对称流动分离现象更显著,二者综合作用下弹体产生额外的侧向力。