冰冲击载荷下螺旋桨轴系动态响应的变参数分析

王 勇 吕 昊 王文全

（1.海军装备部装备项目管理中心 北京100071；2.中国船舶及海洋工程设计研究院 上海200011）

引 言

船舶在冰区航行，漂浮的冰块不仅会与船体发生碰撞，还会与水中工作的螺旋桨接触产生冰载荷，相比于正常工作在敞水中时受到的水动力，巨大冰载荷不仅会对螺旋桨桨叶产生巨大的应力作用，造成桨叶的损坏，进而对推进轴系造成影响，甚至造成推进轴系的破坏。当海冰的位置、大小、速度和密度等不同的参数变化时，海冰和螺旋桨接触的冰载荷必然不同，故而对推进轴系的影响不同。在这种情况下，研究冰参数对轴系的影响情况、发现其中的规律、从而得出相应的结论，对冰区船舶及其螺旋桨、轴系的设计十分必要。国内外学者关于冰载荷对推进轴系影响的研究有很多。耿厚才等［1］得出对于冰区加强船，常规的改变轴系直径、调整飞轮或调频方法难以满足推进轴系稳态扭振应力的要求；杨红军等［2］证明NEWMARK法可较好地用于冰载荷下推进轴系瞬态扭转振动分析；杨红军等［3］表明在冰载荷冲击下，轴系转速有很大的下降，当转速降到一定程度时，扭转振动响应达到最大值；吴帅［4］利用有限元法就冰载荷下轴系振动的固有特性进行研究，得出相位角对轴系扭振响应的影响并非很有规律性；Brown 等［5］通过进行实尺度实验研究表明螺旋桨受到最大扭矩和推进轴系的转矩的比例在0.99 至1.74 的范围内；Dahler［6］研究表明，当螺旋桨受冰载荷超过一定时间后，螺旋桨和推进轴的转矩响应会有明显的差异；Ikonen 等［7］通过使用不同的逆模型提出了螺旋桨桨轴对螺旋桨扭矩的响应变换。DNV·GL［8］（挪威船级社）、IACS［9］（国际船级社）指出冰载荷产生的扭矩分量可表示为敞水水动力扭矩和海冰撞击产生扭矩的和，并可用于冰载荷引起的机械响应变化 ； Polić 等［10］得出的研究为选取最适合的频率和评估工具来转换海冰和螺旋桨载荷对推进轴系响应打下基础。Aki 等［11］对冰载荷下推进轴系激振力动态扭矩进行实尺度模型对比研究。

国内关于冰区螺旋桨轴系的研究资料较少，用于研究轴系结构响应的冰载荷多来自国外学者的研究，这不利于国内关于冰区船舶推进轴系的研究推进；另外国外研究所用的冰载荷集中来自数值统计或者基于冰区航行国家船级社的经验公式，这种载荷与实际情况下船舶推进轴系受到的冰载荷相比更为保守，并且冰载荷在实际情况下变化更为复杂。本文以ANSYS/LS-DYNA 与ABQUAS 为工具建立一套变冰块几何参数工况下，螺旋桨轴系动态响应的数值模拟方法，能较准确地获取冰-桨接触下的动态冰载荷及其变化趋势，具有一定的创新性。

海冰和螺旋桨接触碰撞的过程中，海冰的物理参数直接影响螺旋桨受到的冰载荷大小和冰载荷的变化规律，进而影响船舶推进轴系的工作，因此计算分析海冰参数对冰载荷和推进轴系的影响十分重要。本文利用ANSYS/LS-DYNA 中流固耦合法获取海冰和螺旋桨接触载荷，用ABQUAS隐式有限元法计算该冰载荷对轴系的动态响应，进而分析不同海冰参数（如海冰的位置、尺寸和速度）对推进轴系动态响应的影响规律，为冰区船舶推进轴系的设计、布局以及冰区航行船舶的操纵提供参考意见。

1 数值计算

1.1 理论分析

分析推进轴系在海冰-螺旋桨接触碰撞载荷下的动态响应，其关键在于获取两者耦合作用下的载荷，而海冰-螺旋桨的接触属于流固耦合问题。流固耦合的关键难点在于处理材料的变形行为。一般材料的变形可分为两种类型，变形过程中体积不变和变形过程中体积变化。变形中的应力张量可以分成两部分，即应力偏量和压力。对于任何材料，都可以用应力偏量和压力来描述它的应力张量。在对流体材料处理的过程中，就需要同时使用两种方式来描述材料，用本构模型和状态方程来同时描述一种材料特性：用本构模型来描述应力偏量和压力的关系，用状态方程来描述体积变形和压力之间的关系。在ANSYS/LS-DYNA 中提供一种空材料模式*MAT_NULL 用来描述具有流体行为的材料，改材料模式本身提供本构模型来描述材料的偏应力，然后使用状态方程EOS 来提供压力行为组件，这样它们一起提供材料的整个应力张量。对于每种状态方程，压力都可以表示为比体积和温度的函数方程［12，20］。

NEWMARKS 法是有限元隐式动力分析中主要的分析方法。NEWMARKS 法最初是作为一种常值平均加速度法被提出的，也被看作是线性加速度法的扩展，加时系统的运动微分方程为：

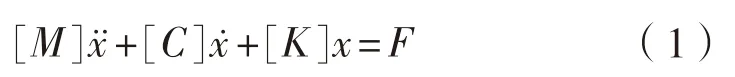
式中：［M］为质量阵 ；［C］为阻尼阵；［K］为刚度阵；F为外力向量。

通过变化运动微分方程，最终可以得到有运动系统质量阵、阻尼阵、刚度阵和外力向量的含假定参数的运动微分方程，通过假定参数的数值范围可以使运动微分方程的解无条件稳定，最终获取系统稳定时的状态。

1.2 数值模型

1.2.1 螺旋桨和推进轴系模型

本文参考加拿大海岸警卫R 级破冰船上装载的四叶1200 系列R-class 冰级桨［13］，选用各方面性能与之相当的ICEPROPELLER-I 设计桨为计算模型，该型螺旋桨为四叶桨，实桨直径为4.1 m、毂径比0.3、盘面比0.67、螺旋桨桨叶后倾10°，计算采用实尺度模型计算（模型如图1 所示）。

图1 螺旋桨网格模型

实际应用中的推进轴系十分复杂，在进行数值分析的过程中适当对其进行简化不仅不影响其动态响应还能提高计算效率。本文在建模过程中进行轴上倒角、孔槽等过渡部位的曲面简化，轴系进行轴承、轴间接触简化，推进轴系重力载荷、油水支撑等载荷的简化施加，从模型和刚度来看各轴承都是单支撑点［14］，然后按照如图2 所示的轴系简图进行推进轴系的模型建立。轴系全长54.2 m，轴系半径为0.5 m，由螺旋桨轴、三段中间轴、尾轴组成，轴段长度分别为12.8 m、12.6 m、9.6 m、9.2 m、10 m。推进轴系总共8 个轴承，从螺旋桨至齿轮箱依次为后托架、前托架、尾轴管轴承、3 个中间轴承、齿轮轴前轴承与后轴承。本文为便于表述，将上述各轴承依次编号为1 号、2 号、3 号、4 号、5 号、6 号、7 号、8 号轴承。各轴承对应的轴承刚度如表1 所示。轴系的材料特性：弹性模量E= 2.1×1011N/m2，泊松比μ= 0.3，密度ρ1= 7 800 kg/m3。

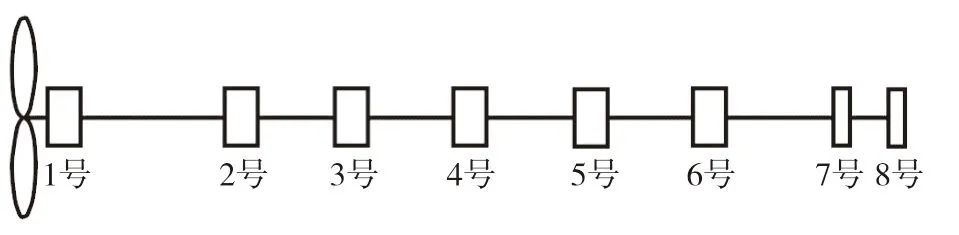
图2 轴系简图

表1 各轴承的刚度N/m

1.2.2 计算工况的设定

本文对海冰的径向位置、海冰冰块大小和海冰速度大小进行变参数计算，关于海冰和螺旋桨接触的冰载荷是在LS-DYNA 中获取。本文中海冰采取正六面体空间形状进行海冰和螺旋桨碰撞的数值模拟；同时，变参数海冰的网格的划分皆采用一种方式进行划分以确保变量的统一；为兼顾求解结果的准确性和求解效率，经过多次计算比较，选择0.04 m 的网格密度对海冰进行划分。

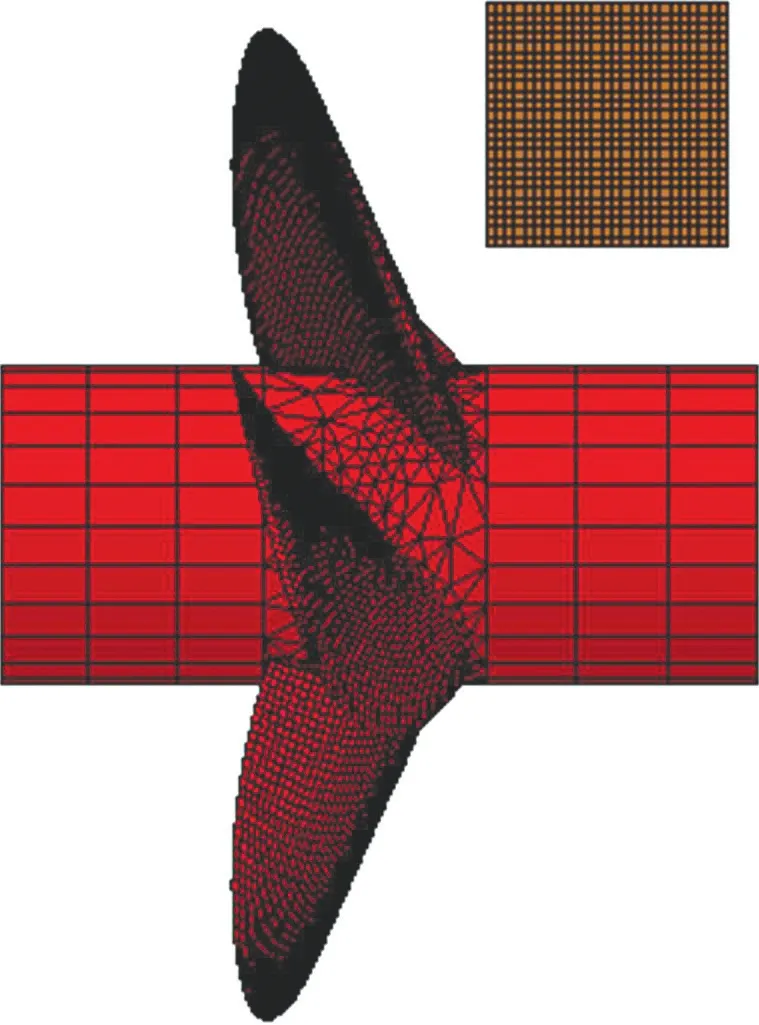
图3 海冰与螺旋桨的相对位置

对于海冰在螺旋桨不同径向位置的模型如下页图3 所示，海冰位置以海冰中心位置距离桨轴中线的径向垂直距离为准，径向垂直距离以螺旋桨半径（R）基准，分别取0.8R、0.9R和1.0R，螺旋桨转速统一取30 r/min，海冰前进速度与流域速度均为1.2 m/s，海冰边长1.0 m。通过改变正六面体海冰的边长进行海冰大小的变参数模型建立，海冰边长分别取0.80 m、1.00 m 和1.25 m，海冰的径向位置统一取0.9R，海冰前进速度与流域速度均为1.2 m/s，螺旋桨转速为30 r/min；海冰的速度可以通过软件速度参数设置进行控制从而获取其冰载荷，海冰速度取0.8 m/s、1.2 m/s 和1.6 m/s，海冰随流域的速度改变而改变，流域速度与海冰一致，海冰边长统一取1.0 m，海冰径向位置统一取0.9R，螺旋桨转速仍统一取30 r/min。

2 变参数分析

2.1 海冰-螺旋桨耦合动态分析

为验证本文获取海冰和螺旋桨接触碰撞载荷方法的正确性，本文结合Kim 的球型冰冲击试验［15］进行数值模拟验证，图4 为计算模型、图5为数值验证。通过和Kim 的实验对比发现获取的载荷和实验符合程度较好，证明本文获取冰载荷的方法是正确的。计算海冰边长1.0 m、速度1.2 m/s、海冰径向0.9R时螺旋桨的冰载荷曲线，提取冰载荷中轴向力Fx、垂向力Fz、轴向弯矩Mx和水平弯矩My，各个力学分量的示意图如图6 所示，计算结果参见下页图7。

图4 冲击计算模型

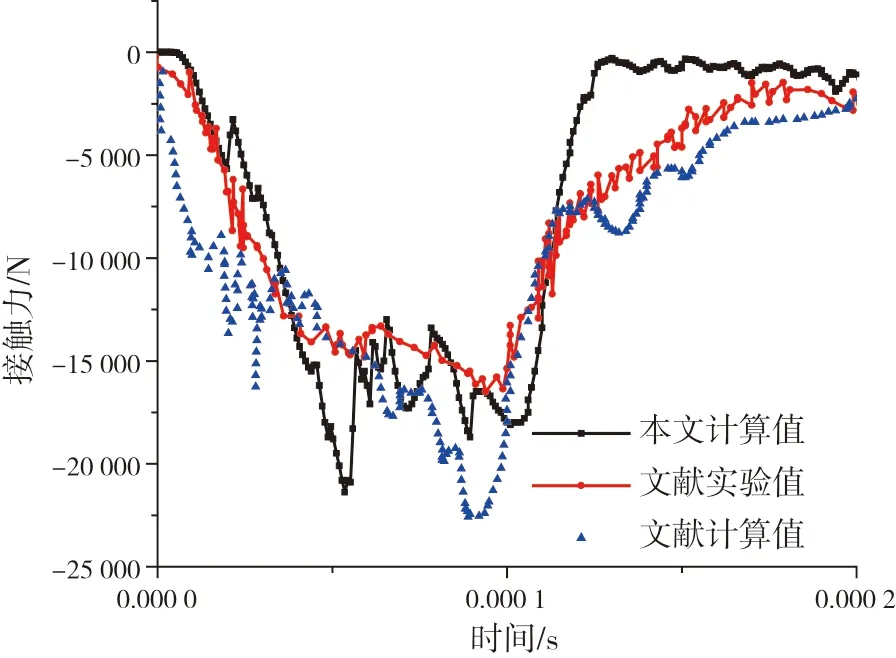
图5 接触力时程曲线

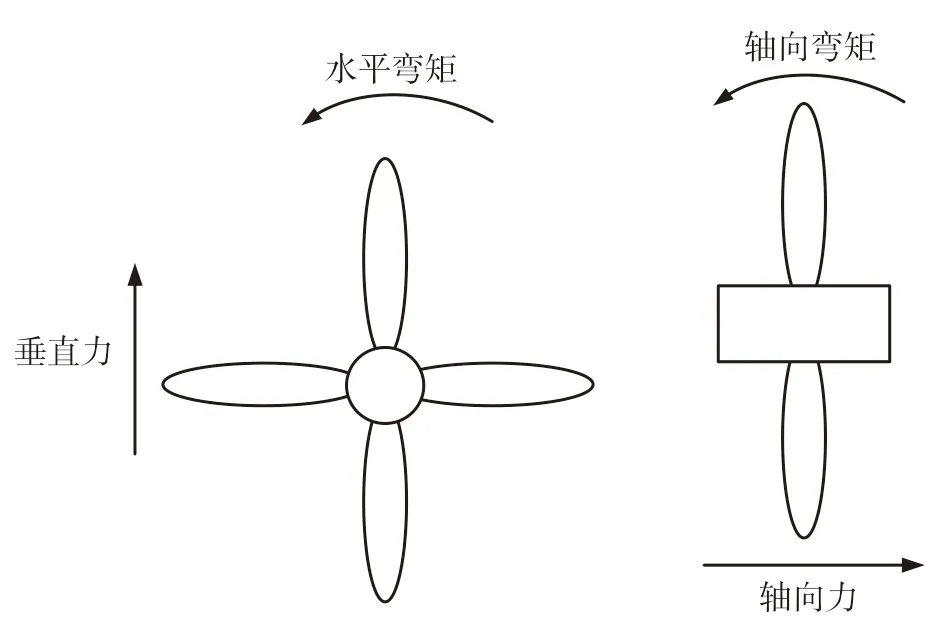
图6 螺旋桨所受力和弯矩示意图

把力和力矩结果输入ABQUAS运用NEWMARKS法，计算得到推进轴系轴承、推进轴的动态响应情况，分析海冰-螺旋桨接触载荷对螺旋桨和轴系的影响计算得到不同轴承的等效应力（即屈服准则的值）、应变以及扭矩响应时域图，通过对比得知冰载荷对尾托架即1 号轴承的影响最大，故在进行海冰不同参数产生的冰载荷对轴系的影响时，以1 号轴承作为分析的重点，其动态响应图如图8所示。

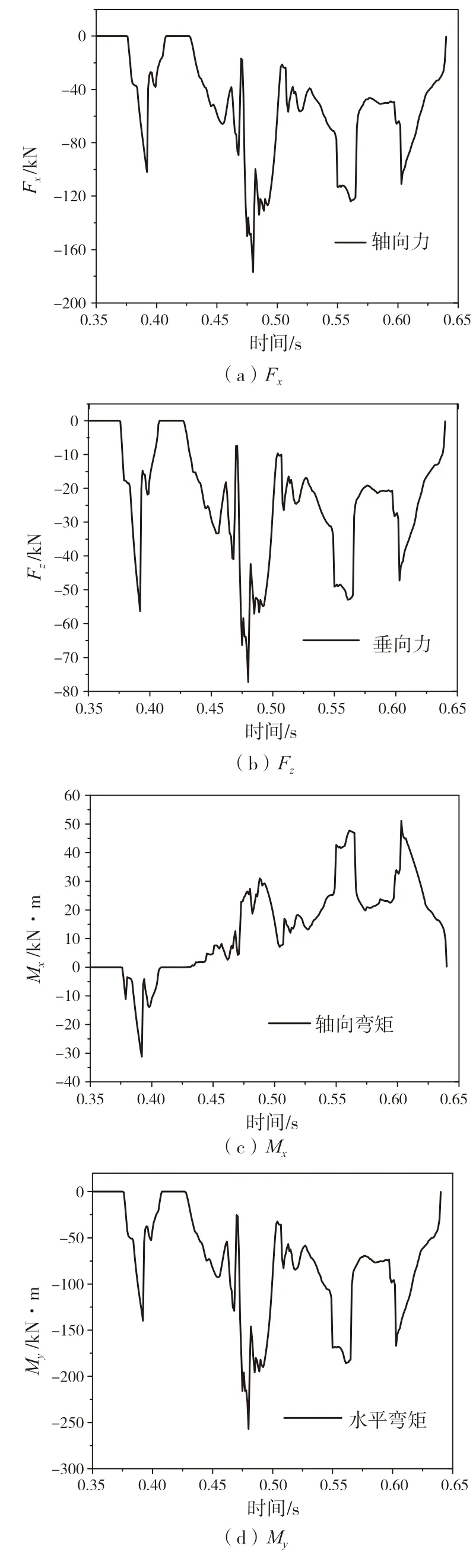
图7 冰载荷时间历程曲线

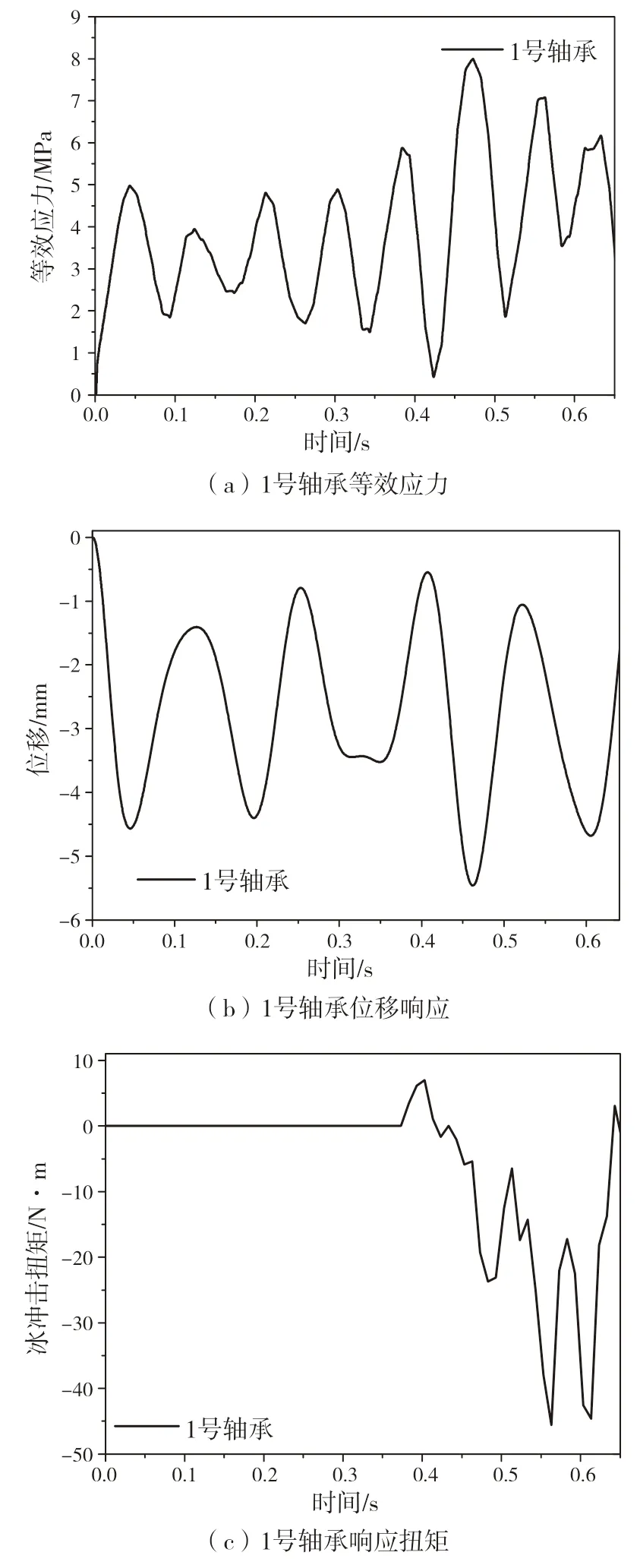
图8 1号轴承动态响应图

2.2 海冰不同径向位置轴系动力响应分析

计算得到海冰和螺旋桨接触下冰载荷，提取冰载荷的轴向力Fx、垂向力Fz、轴向弯矩Mx、水平弯矩My，得到如图9 所示的海冰不同径向位置冰载荷时间历程曲线。图中A、B、C三点分别是位于不同半径处的冰块和螺旋桨接触的时刻，分别为0.278 s、0.369 5 s、0.477 s。海冰越靠近桨轴中心线，与桨叶接触时间越早，反之则越晚。表2 给出冰载荷不同分量在冰桨接触过程中的峰值及不同半径处峰值对比结果，其表明改变海冰径向位置对冰载荷的轴向力、垂向力影响较大。对于不同径向位置的海冰，虽然海冰的强度相同，但海冰和螺旋桨接触面积与两者间的碰撞角度不同，从而导致两者的接触冰载荷不同。

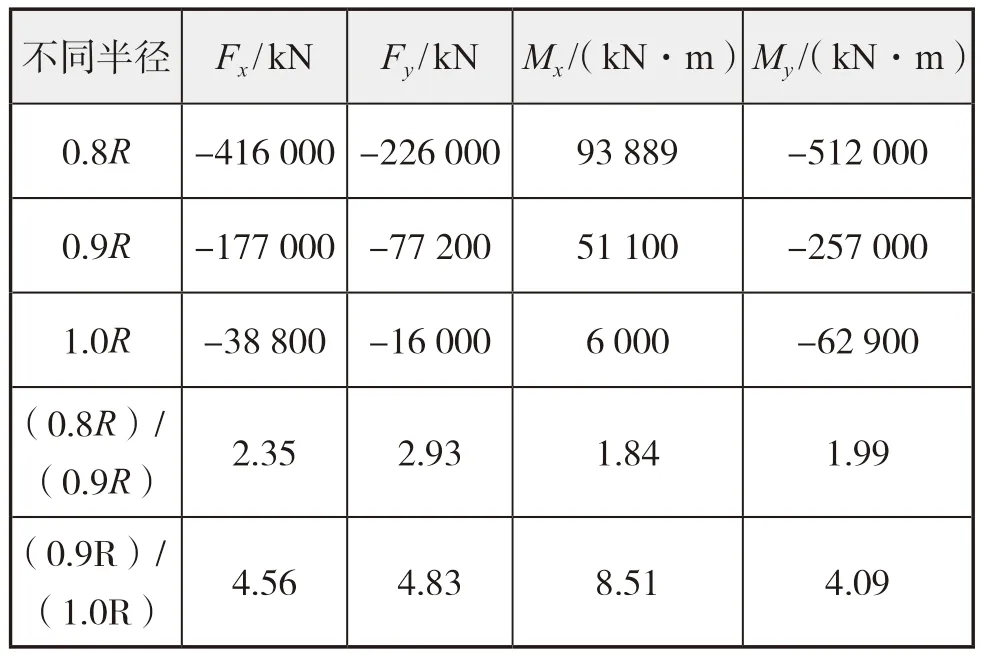
表2 海冰位于不同半径处的冰载荷分量峰值

图9 为海冰不同径向位置冰载荷时间历程曲线。从图中可以看出，海冰位于0.8R处时，海冰和螺旋桨的接触时间大于海冰位于0.9R处的，0.9R处的又大于1.0R处。可见，越靠近桨轴中心线，海冰脱离桨盘面的时间越久，海冰和螺旋桨接触时间越久，会导致螺旋桨切入海冰的深度增加，最终导致海冰和螺旋桨接触面积增加以及海冰和螺旋桨接触载荷增加；这也说明图中越靠近桨轴中线，海冰和螺旋桨接触载荷峰值出现的时间越早，且峰值越大。

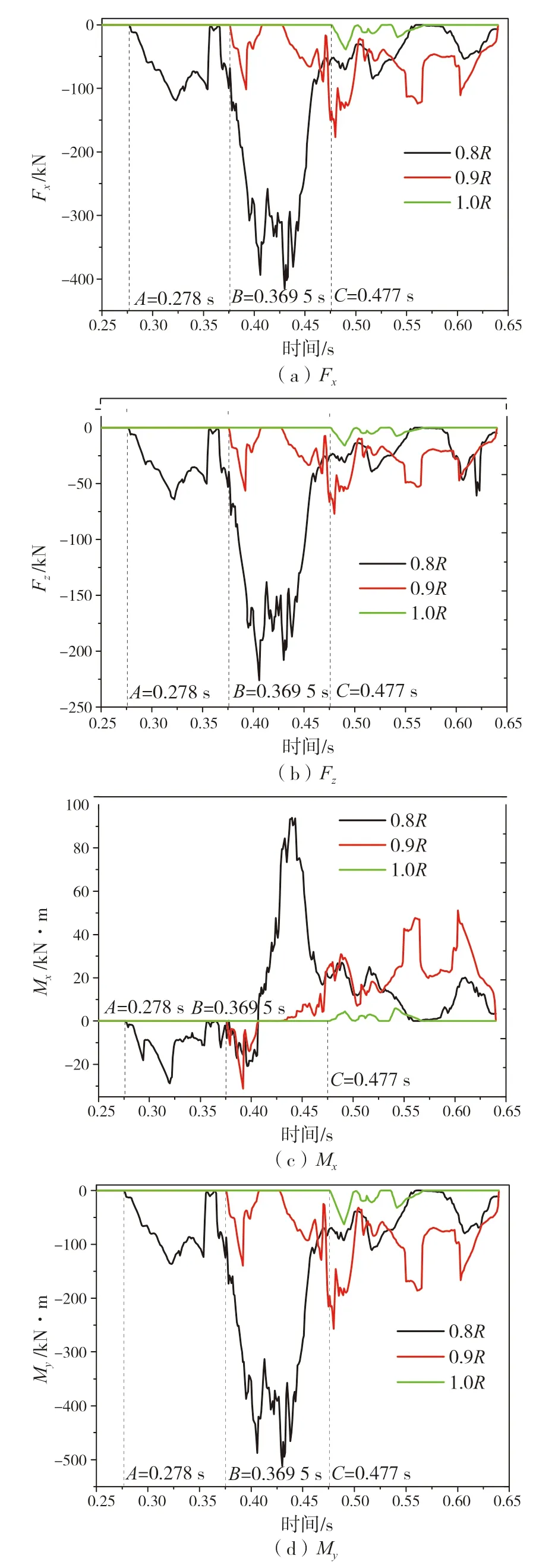
图9 海冰不同径向位置冰载荷时间历程曲线

冰载荷下的轴系动态响应中，1 号轴承（后托架轴承）所受冰载荷的影响最大。下页图10 是海冰不同位置冰载荷下，后托架轴承的位移、等效应力和响应扭矩时域图，表3 给出不同径向处的最大位移、最大等效应力和最大扭矩结果。

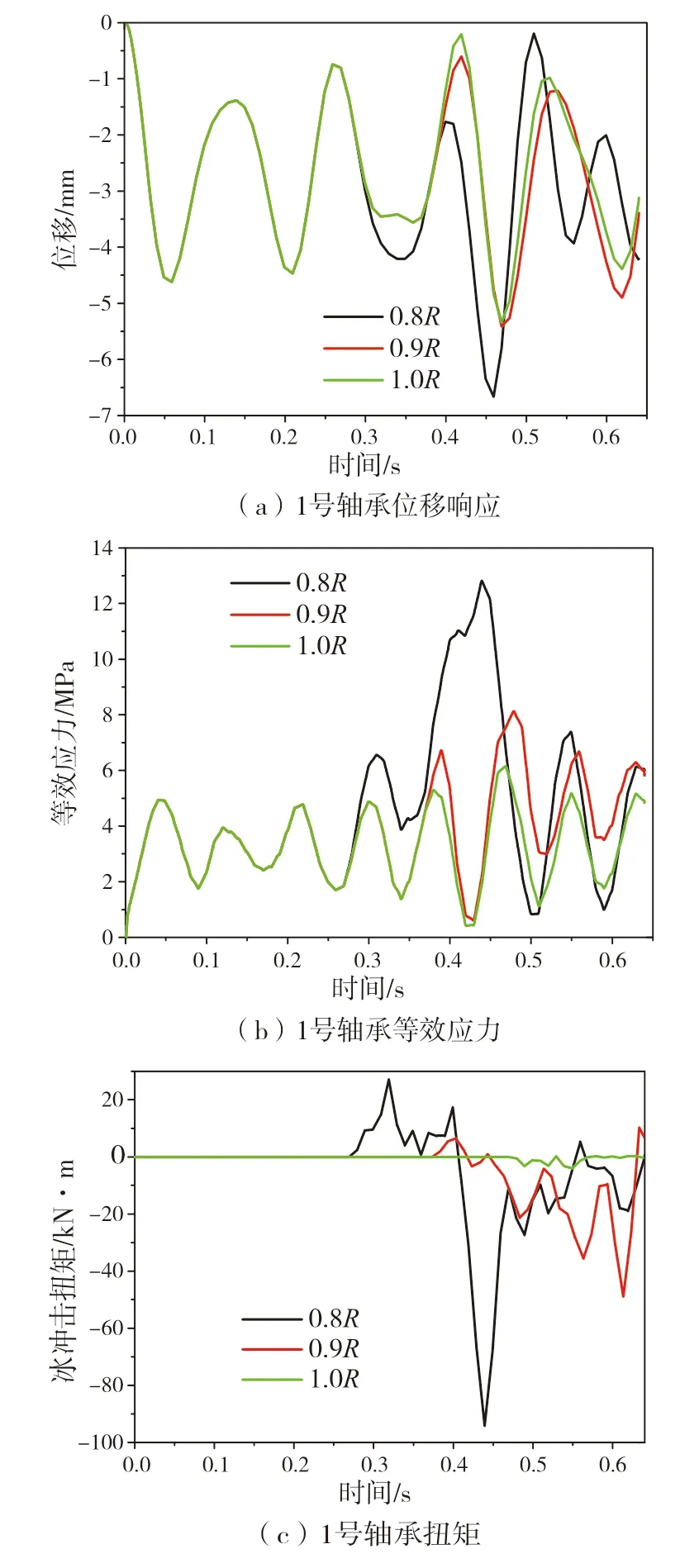
图10 海冰不同位置冰载荷下1号轴承动态响应时域图

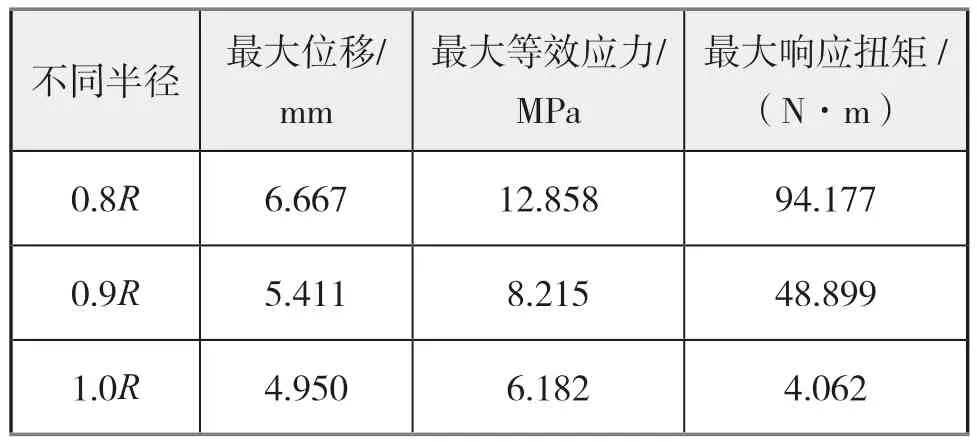
表3 海冰位于不同径向处的1号轴承动态响应值

从计算结果来看：推进轴系遭受的载荷或结构响应的极值的时刻与冰桨接触碰撞的时刻大抵一致。由此可推断，冰桨碰撞产生的载荷会显著影响推进轴系，尤其可以看出随着海冰与螺旋桨的径向相对位置减小或者海冰在桨盘面的投影面积增大，轴系的结构响应也随之增大，而海冰和螺旋桨径向相对位置的减小或海冰在桨盘面投影面积的增大是冰桨碰撞载荷增加的直观体现。由此可知，轴系的结构响应与冰桨碰撞载荷成正比。由该图可见，在海冰尺寸相同的情况下，海冰轴向位置愈靠近桨轴中心，两者之间碰撞接触的时间愈长，碰撞载荷亦愈大，故而轴系的结构响应幅值越大。把简化的轴系看视为一根悬臂梁，则可以推断在更长且更大的冰载荷条件下，轴系的变形必然是最显而易见的；冰桨之间的载荷主要以扭矩的方式传递至轴系，且与载荷成正线性相关。

2.3 海冰不同尺寸轴系动力响应分析

轴系的动力响应不仅和海冰径向位置有关，还与海冰的尺寸有关，在实际航行状态下，推进轴系遭遇的海冰尺寸具有一定的随机性，与其航行水域的海冰分布有关系［14-16］。不同航行区域的海冰因为气候环境、水文环境等原因导致冰的大小不同，所以研究不同尺寸海冰对轴系的影响十分必要。

下页图11 给出不同海冰尺寸下的冰载荷分量的时域曲线图。从中可看出：海冰边长0.8 m 时海冰和螺旋桨接触时间最晚，碰撞周期最短，接触力也是最小，冰载荷的最大值随着海冰尺寸的增大而逐步上升，产生这一现象的原因是海冰的尺寸越大，海冰和螺旋桨铣削时的接触面积越大，导致冰载荷力越大；同理，海冰尺寸越大，海冰和螺旋桨接触的时间越早。从轴向力、垂向力的时域曲线上可以发现，海冰边长1.25 m 的情况下冰载荷达到峰值的时间最短，碰撞周期最长，说明海冰尺寸的增大导致海冰和螺旋桨碰撞过程中相对速度的增大和接触面积的增大。

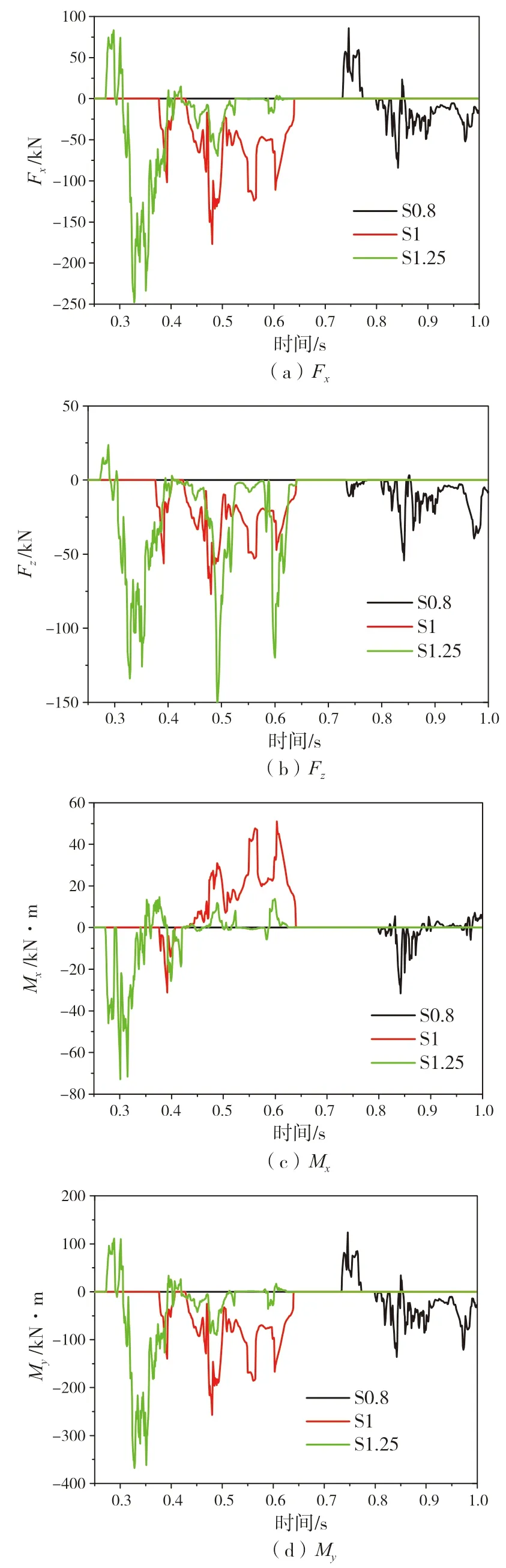
图11 海冰不同尺寸冰载荷时间历程曲线

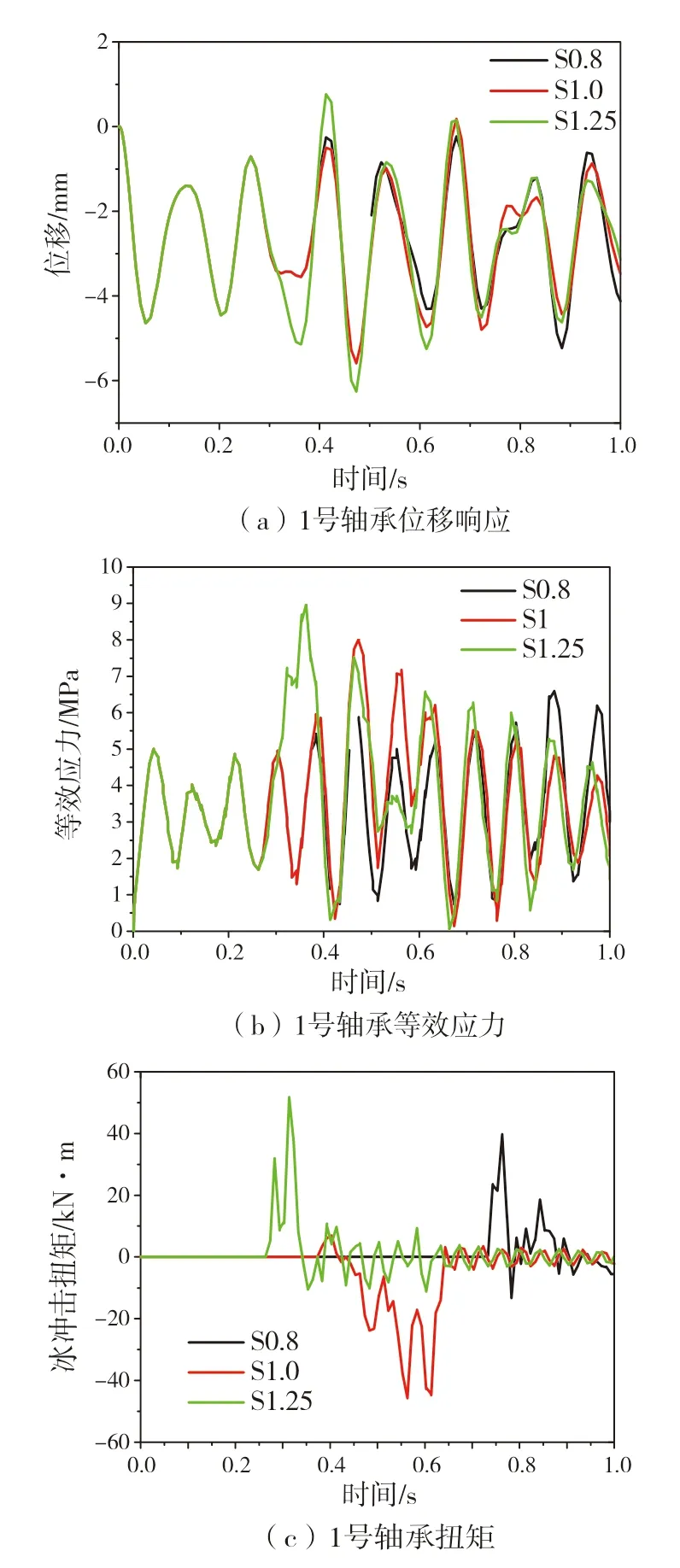
图12 海冰不同尺寸冰载荷下后托架动态响应时域图

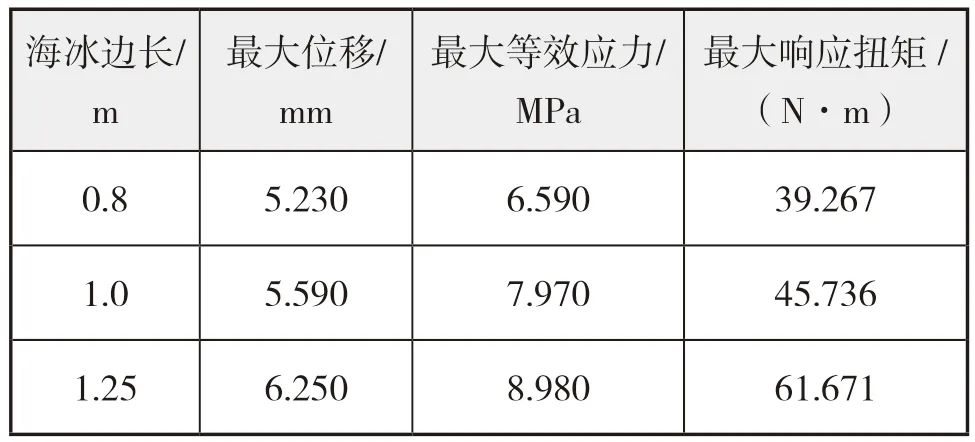
表4 不同海冰边长下的1号轴承动态响应最大值

海冰尺寸不同时后托架轴承动态响应如图12所示，各参数的最值如表4 所示。通过对比分析图12 和表4 可以发现本文计算选用的轴系直径较大。从中可以看出：以海冰边长为1.25 m 为临界，当海冰尺寸小于此值时，冰桨之间的碰撞载荷明显小于海冰尺寸大于该值时，但无论哪种海冰尺寸，轴系响应的极值与冰桨碰撞载荷的极值出现的时刻基本一致，说明两者的碰撞载荷对轴系影响较为显著，也从侧面证明冰桨之间的接触面积愈大，两者之间的碰撞载荷也愈大。

2.4 海冰不同速度下的结果分析

船舶在不同海域航行，受风、流等气象因素以及船舶航行速度、状态等影响，海冰与螺旋桨接触时的速度也不一样［14-16］。本节计算不同海冰速度下的海冰和螺旋桨接触冰载荷冰，并提取轴向力Fx、垂向力Fz、轴向弯矩Mx、水平弯矩My时域变化曲线（如图13 所示）。

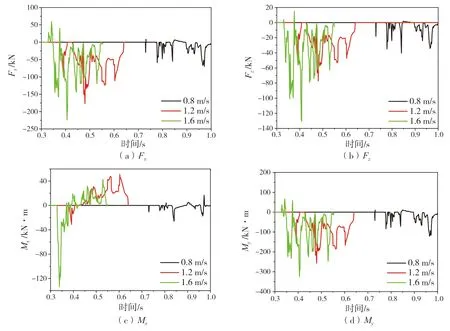
图13 海冰不同速度冰载荷时间历程曲线

由结果可知，海冰移动速度相同且为低速，冰桨之间的相对距离比其他速度时更长，进而可以推断冰桨接触之前螺旋桨的相对旋转位置与海冰移动速度高时不同。结合图14 可以看出：冰桨的接触位置由高速时的桨叶1 转换为桨叶2，从而出现在图13 中海冰移动速度较低时，冰桨之间的碰撞载荷出现时刻比其他两个工况晚；另外，由于海冰的移动速度不同进而造成海冰和螺旋桨发生碰撞的位置不同，直接造成两者之间的碰撞载荷不同。

从图13 中可以看出：海冰移动速度最大时，冰桨之间的碰撞载荷持续时间最短；并且载荷如轴向力、垂向力均值较其他两个航速工况更大。从海冰自身角度来讲，由于海冰的移动速度增大，其自身的动能增大，接着导致冰桨接触时的碰撞载荷增大，螺旋桨和轴系由此产生的结构响应增大，这同上面的载荷曲线变化相吻合。

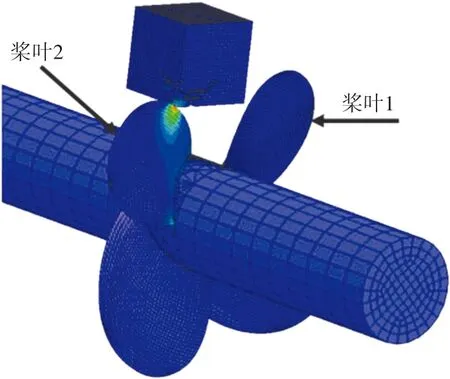
图14 冰桨接触

图15 是海冰速度不同时，后托架的动态响应时域图，表5 对应为各参数曲线的最大值。对比图15（a）中曲线可知，后托架轴承的位移值为负，说明轴系向下进行动态响应；海冰速度为0.8 m/s时，后托架的位移时域曲线较为均匀平缓，但在t= 0.47 s 时刻，三种海冰速度下，后托架的位移皆出现一个较大的峰值。对于海冰速度为1.2 m/s 和1.6 m/s 的情况，由于冰载荷在该时刻存在峰值，故可能由于冰载荷峰值原因致使位移曲线出现峰值；对于海冰速度为0.8 m/s 的情况，由于这个时刻海冰和螺旋桨还未接触，所以可能是阻塞效应造成的螺旋桨冰载荷的增加，进而导致后托架轴承位移响应出现峰值。结合下页表5 可知轴承的最大位移值并不是特别大，主要原因仍是该推进轴自身较粗，与实际船舶的推进轴存在差异，导致数值计算结果偏于保守。如何能更贴近实际的建模计算，则是后续的研究工作。由图15（b）可看出，海冰速度为1.6 m/s 时，后托架轴承等效应力的整体曲线对比以上两种速度工况幅值有明显增大，且在这种工况下托架轴承的等效应力达到最大，其主要是冰所获得的动能转化为轴系自身的变形能所造成的，即转化为较大的冰载荷。形成的冰载荷增加了托架轴承所受的等效应力和水平弯矩。同时，由以上分析可知，水平弯矩在海冰行进速度最大时达到最大，所以等效应力的最大值也应在海冰速度为1.6 m/s 时。由表4 后托架轴承最大等效应力随工况变化的曲线变化趋势也可以看出，海冰行进速度第二次增加导致的幅度增长小于第一次海冰速度增长。由图15（c）得出使轴系发生扭转变形的主要原因是冰激励扭矩，冰激励扭矩正负交替变化造成了抗扭矩也产生相应地变化；通过后托架最大响应扭矩随海冰速度变化图，发现响应扭矩的最大值与海冰行进速度基本成二次相关，在海冰行进速度为1.6 m/s 时所产生的最大扭矩值大约为行进速度是0.8 m/s 所产生的扭矩7 倍；轴系的抗冰载荷扭矩取决于冰激励扭矩的大小，冰激励扭矩的增加会使轴系为维持原来形状不变而产生抗冰载荷扭矩。

图15 海冰不同速度时后托架轴承动态响应时域图

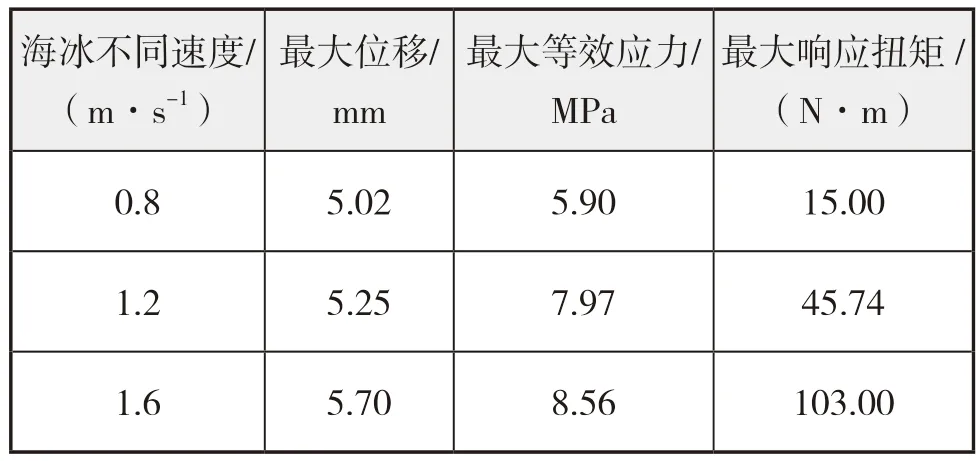
表5 不同海冰速度下的1号轴承动态响应最大值

3 结 论

本文基于采用流固耦合和有限元方法，就海冰和螺旋桨碰撞下轴系动态响应进行冰参数变化计算分析，并得出如下结论：

（1）冰桨之间的碰撞产生的冰载荷会对推进系统的轴系产生维系，尤其在推进轴系尾端靠近螺旋桨位置处的轴承结构安全威胁较大，会引起其产生剧烈的应力及位移变化。

（2）海冰与螺旋桨的相对位置越接近，即海冰与螺旋桨间的径向相对位置或海冰在桨盘面的投影面积越大，造成两者间碰撞载荷越大，从而增加轴系损坏的风险。因此在极地海冰较多的地区，不仅需要对螺旋桨的结构强度进行加强，保证推进系统轴系的强度对保证船舶安全也十分重要。

（3）通过上述分析可知，推进轴系后托架是整个推进轴系在遭遇冰载荷过程中最容易遭受损坏的部分；因此在轴系的设计过程中，如何加强和保证这部分的结构性能安全需要船舶设计者重点考虑，这同时也是本文写作的初衷。

本文建立的数值计算模型与实际情况相比，由于作了较大简化，因此导致计算结果与实际存在一定误差，但也由此总结出一套研究变参数的方法，并初步获得不同冰参数对轴系的影响情况，而后，我们将进一步完善数值计算模型并增加计算精度。