往复泵十字头轴承疲劳寿命计算
郑祥,陈宇,宁小波,王玉勤
(巢湖学院 机械工程学院,安徽 巢湖,238000)
滚动轴承由于受力情况比较复杂,统计数据显示旋转机械中约30% 的机械故障是由滚动轴承的失效引起,轴承的寿命计算一直是工程中的热点研究问题[1]。孙玉凤等[2]利用有限元分析软件对调心滚子轴承接触应力进行数值模拟分析;宋博峰[3]通过对圆锥滚子轴承30207为研究对象,推出了外滚道接触刚度系数的计算公式。十字头轴承是往复泵中重要的传动部件,在工作过程中承受到的是交变载荷,文章通过建立往复泵传动端的运动模型,求解出十字头轴承的载荷曲线,进而得到轴承的平均当量动载荷,计算出可靠度为90%时的轴承疲劳寿命。
1 往复泵十字头载荷计算
往复泵主要由传动端和液力端组成,图1为某型号的三缸单作用往复泵的结构示意图。外部动力源通过人字齿轮轴5输入动力,经过与曲轴1上的大齿圈6啮合,实现泵内减速及动力的传递,从而带动连杆2的平面摆动及十字头3和活塞部件4的直线运动,实现往复泵的吸入及排除行程。十字头是传动端重要的零部件,将连杆的运动和力传递给活塞部件,十字头轴承是整个功能实现的核心。

1-曲轴;2-连杆;3-十字头;4-活塞杆组件;5-人字齿轮轴(输入轴);6-人字齿圈(曲轴)图1 往复泵传动端结构简图Fig.1 Structure diagram of transmission end of a reciprocating pump
1.1 建立运动模型
十字头带动活塞做往复直线运动,为了便于分析,简化成一个曲柄滑块机构,如图2所示。图中,OA为曲柄、AB为连杆,其中C是连杆的质心,A是连杆大端,B是连杆小端。

图2 十字头运动示意图Fig.2 Cross-head motion diagram
建立平面运动微分方程[4],易得十字头的位移方程s、速度方程u、加速度方程a。
(1)
(2)
(3)
式中:R为曲柄半径;λ为连杆比,λ=R/L(L连杆AB的长度);ω为曲柄角速度;φ为曲柄转角,φ=ωt。
连杆AB的平面运动可以等效为绕其质心C(xc,yc)作平动和定轴转动的组合,易得连杆的运动方程。
(4)
yc=Rsinφ-L1sinδ=Rsinωt-L1λsinωt
(5)
δ=arcsin(λsinφ)=arcsin(λωt)
(6)
式中:δ为连杆的摆角。
连杆质心C点的加速度分量acx、acy及角加速度εc。
(7)
(8)
(9)
1.2 十字头载荷计算
图3是传动端平面力系简图。其中,十字头和连杆自重分别为m2g和m3g;十字头受到连杆小端的力F1x和F1y、滑履的力F2x和F2y;曲轴受到连杆大端的力F3x和F3y。

图3 往复泵传动机构的平面力系Fig.3 Plane force system of transmission mechanism of reciprocating pump
根据刚体平面运动方程可得[4],F1x和F1y。
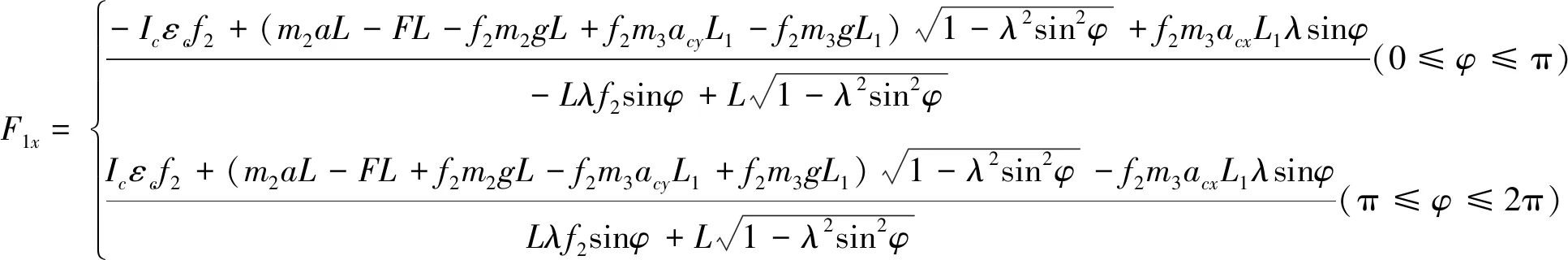
式中:f2为十字头运动副的滑动摩擦系数;
F为活塞的介质力;
Ic为连杆在质心C处的转动惯量,kg·m2;
F1为十字头轴承所承受的载荷,N。
往复泵的性能参数选自型号为W-446的三缸单作用泥浆泵,具体参数见表1。
表1 往复泵性能参数
Table1 Related parameters of a reciprocating pump

参数名称参数值曲柄半径R/m0.076活塞行程s/m0.152连杆长度L/m0.605连杆比λ0.126连杆质量m3/kg77.349连杆大端到质心的长度L1/m0.138连杆对质心C的转动惯量Ic/(kg·m2)6.755十字头组件质量m2/kg72.899D缸套内径/m0.152缸套内孔面积A/m20.018活塞冲次n/(次/min)220曲柄角速度ω/(rad/s)23.038十字头与滑履之间的滑动摩擦系数f20.1额定排出压力p/MPa9.17
带入计算数据可得十字头载荷F1与曲柄转角关系图。
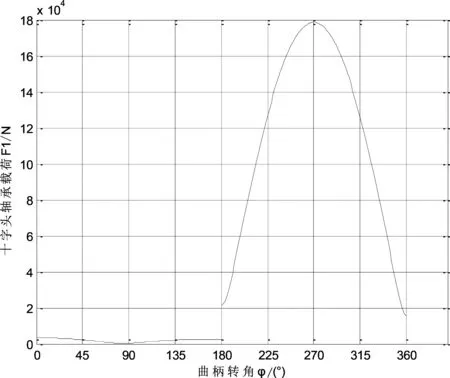
图4 十字头载荷F1与曲柄转角关系Fig.4 The relationship between cross-head load and crank rotation angle
令
一个活塞行程中,当曲柄转角φ≈269°,十字头轴承承受的最大载荷F1max=178 660 N。
2 十字头轴承寿命计算
往复泵中滚动轴承的失效形式主要有表面疲劳破坏和表面磨损两种,磨损失效的寿命仍没有可靠的计算方法[5],文中采用疲劳破坏的方法来计算轴承寿命。
2.1 十字头轴承基本额定动载荷计算
十字头轴承承受的载荷具有交变性、周期性,要计算轴承的寿命,必须要获得轴承的基本额定动载荷[5]Cr。
式中:bm为系数,bm=1;fc为系数,fc=76.564;i为滚针列数,i=2;α为接触角,α=0°;Z为滚针个数,Z=70;Dwe为滚针直径,Dwe=5 mm;Lwe为滚针有效长度,Lwe=17.56 mm。
该型号往复泵十字头轴承为双列滚针轴承NA6914,带入数据。
基本额定动载荷为Cr=166.2 kN。
2.2 十字头轴承平均当量动载荷计算Pm
当轴承受变载荷时,因为活塞吸入行程和排除行程轴承载荷属于不同函数曲线,并且φ=π处函数曲线不连续,所以采用分段积分计算轴承的平均当量动载荷Pm。
2.3 十字头轴承疲劳寿命计算
以疲劳破坏为条件的滚动轴承寿命计算早已获得公认,当可靠度为90%时的寿命计算公式如下式[5]。

式中:Lh为可靠度为90%时轴承的疲劳寿命,h;n为十字头轴承的转速,n=250 r/min。
所以,型号为NA6914双列滚针轴承,可靠度为90%时的十字头轴承疲劳寿命为292 h。
3 小结
通过对往复泵十字头进行运动学分析,从而建立刚体平面力系方程,推导出十字头所受载荷与曲柄转角间的关系曲线图,在此基础上获得十字头轴承载荷最大时曲柄的转角值。利用分段积分得到十字头轴承平均当量动载荷。最后计算出可靠度为90%时十字头轴承的疲劳寿命。文章的计算过程中,未充分考虑轴承的流体动压油膜及弹性变形[6-7]的影响,有待进一步的分析与研究。

