巧点妙拨方能化蛹成蝶

陆娟

摘 要：帮助学生积累数学活动经验是数学教学的重要目标。在教学中，教师巧妙的点拨能让学生感悟数学的基本思想，积累数学思维活动和实践活动的经验。

关键词：数学活动;点拨;培养思维;感悟方法

中图分类号：G633.6          文献标识码：A

文章编号：1992-7711（2019）21-071-2

不少数学教师教学时常感到自己教得费劲，学生学得吃力，长期困恼大多数老师的是：怎么才讲过的知识点一做题就又错了？其实，这要从教师的教学方法中找原因。传统的数学课堂教学一般由教师问，学生答，教师问什么，学生答什么。活动形式相对单一，学生的思维很封闭，没有伸缩的空间。有人形容传统的数学教学是“带着镣铐在跳舞”，久而久之学生的思维逐渐变成“直线型”。

一、实践探索

1.巧点妙拨，积累数学活动经验

苏科版九上《学习与评价》P60探索与研究：如图1是某学校存放学生自行车的车棚的示意图（尺寸如图所示），车棚顶部是圆柱侧面的一部分;图2是车棚顶部截面的示意图，AB所在圆的圆心为O，车棚顶部是用一种帆布覆盖的，求覆盖棚顶的帆布的面积（不考虑接缝等因素，计算结果保留π）。

批改作业的过程中我统计了两个班大概有1/4的同学不会或者做错，就本题我先设问：①覆盖棚顶的帆布面积这一实际问题转成数学问题其实质是什么？（生：侧面展开图的面积）;②怎样求侧面展开图的面积？（生：原来问题的实质是求弓形的弧长）③该题中有我们熟悉的数学思想或数学模型吗？（生：作垂直根据垂径定理得直角三角形用勾股定理解决问题）

解题是对问题中所含信息的提取、组织、加工的过程，是对已有基本知识、基本活动经验的综合应用过程、解题过程能否顺利进行受到许多因素的影响，如：对问题的熟悉程度、原有的知识经验及观察能力、归纳概括能力、元认知能力等。所以通过解题反思强化基本活动经验：①将实际问题抽象为对应的数学问题;②抽象出解决数学问题的基本模型。

用这样积累的活动经验可以继续解决苏科版九上《学习与评价》P67应用与延伸：工人师傅为了检测该厂生产的一种铁球的大小是否符合要求，设计了一个工件槽（如图），其中工件槽的两个底角均为90°，尺寸如图（单位：cm）。将形状规则的铁球放入槽内时，若同时具有图中的A、B、E三个接触点，该球的大小就符合要求。请结合图中的数据，计算符合要求的铁球的直径。

2.巧点妙拨，感悟数学思想方法

《数学课程标准（2011年版）》指出：“数学思想蕴涵在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概况，在义务教育阶段应结合具体的教学内容逐步渗透数学的基本思想。

苏科版九上《学习与评价》P66的填空题（5）如图1、图2、图3分别是边长均大于2的三角形、四边形、凸n边形。分别以它们的各顶点为圆心，以1为半径画弧与两邻边相交，得到3条弧、4条弧、n条弧。图1中3条弧的弧长的和为    ，图2中4条弧的弧长的和为    ，图3中n条弧的弧长的和    （用n表示）。

这题有将近1/5的同学不会，这次我没有直接设计问题启发他们思考，而是让他们把回看：苏科版九上《学习与评价》P58的填空题（3）如图，⊙A、⊙B、⊙C两两不相交，且半径都是1cm，则图中的三个扇形（即阴影部分）的面积之和为   cm2。

先将两题一起回看然后完成这样的流程：“读——理解感悟（题意）”、“疑——比较鉴别（异同）”、“做——解决问题（数学化）”、“说——交流思想（积累经验 形成方法）”。

在学生完成上面自我领悟、反思碰撞的过程之后，我又继续追问：求阴影部分面积这题可以继续变式吗？于是类比弧长模型，學生很快设置了如下问题：图中四个扇形（即阴影部分）的面积之和为    cm2;……图中n个扇形（即阴影部分）的面积之和为    cm2。

二、回顾反思

1.积累数学活动经验，重在“做”

《数学课程标准（2011年版）》特别强调：“数学活动经验的积累是提高学生数学素养的重要标志。帮助学生积累数学活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动过程的结果。”积累数学活动经验的目的之一是建立数学的感悟、数学的直观。

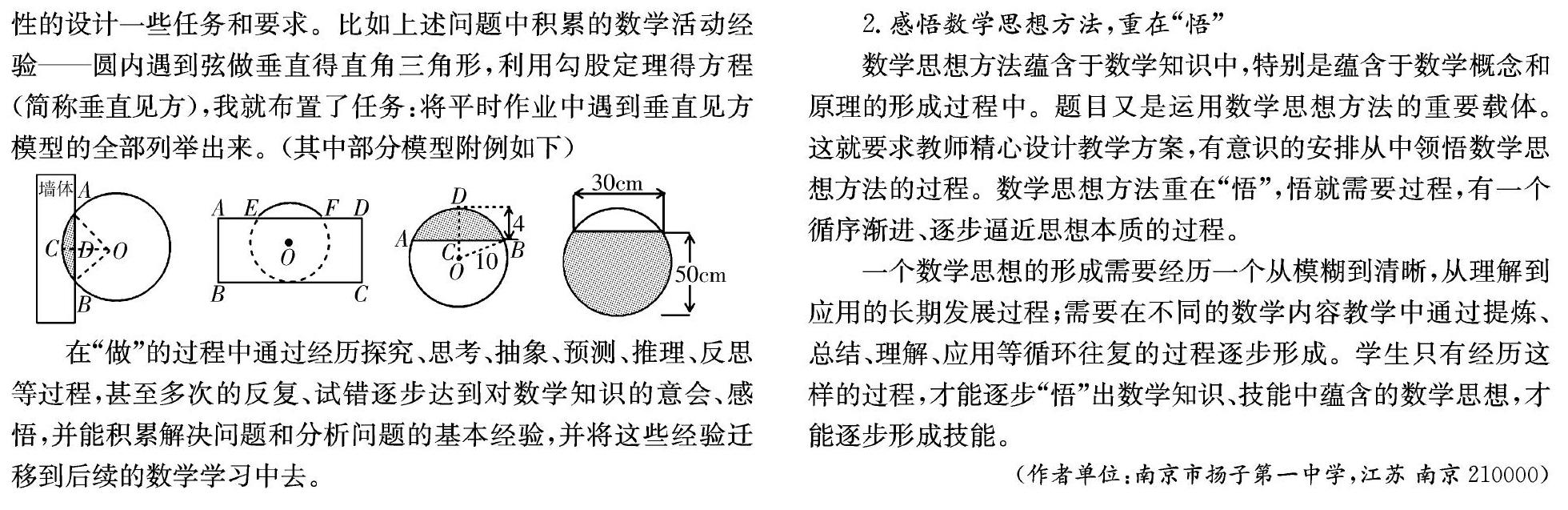
这个需要我们老师在平时的教学过程中多引导，甚至有指导性的设计一些任务和要求。比如上述问题中积累的数学活动经验——圆内遇到弦做垂直得直角三角形，利用勾股定理得方程（简称垂直见方），我就布置了任务：将平时作业中遇到垂直见方模型的全部列举出来。（其中部分模型附例如下）

在“做”的过程中通过经历探究、思考、抽象、预测、推理、反思等过程，甚至多次的反复、试错逐步达到对数学知识的意会、感悟，并能积累解决问题和分析问题的基本经验，并将这些经验迁移到后续的数学学习中去。

2.感悟数学思想方法，重在“悟”

数学思想方法蕴含于数学知识中，特别是蕴含于数学概念和原理的形成过程中。题目又是运用数学思想方法的重要载体。这就要求教师精心设计教学方案，有意识的安排从中领悟数学思想方法的过程。数学思想方法重在“悟”，悟就需要过程，有一个循序渐进、逐步逼近思想本质的过程。

一个数学思想的形成需要经历一个从模糊到清晰，从理解到应用的长期发展过程;需要在不同的数学内容教学中通过提炼、总结、理解、应用等循环往复的过程逐步形成。学生只有经历这样的过程，才能逐步“悟”出数学知识、技能中蕴含的数学思想，才能逐步形成技能。

（作者单位：南京市扬子第一中学，江苏 南京210000）