基于非零均值比的RS 码盲识别方法

龙 浪 杨俊安 刘 辉 梁宗伟

（1.国防科技大学电子对抗学院，合肥，230037；2.安徽省电子制约技术重点实验室，合肥，230037）

引 言

在数字通信中，信道编码可以提高通信的可靠性，目前信道编码主要包括线性分组码、RS（Reed-Solomon）码、卷积码和低密度校验码（Low-density parity-check，LDPC）码等[1-2]，其中RS码是一种特殊的非二进制BCH（Bose-Chaudhuri-Hocquenghem）码，具有纠错能力强的特点，在数据存储、军事通信、卫星通信和数字视频广播（Digital video broadcasting，DVB）系统中起着至关重要的作用。因此，研究RS码的盲识别方法有重要意义。

现有文献表明，国内外已有大量学者对RS码盲识别算法展开研究。文献[3]对各种非二进制纠错码的码长进行了盲识别，并扩展到有噪环境下的研究,但未对RS码其他编码参数进行识别。文献[4]在文献[5]对偶码的识别基础上研究了有噪环境下的RS码盲识别，但算法抗误码性能不佳。文献[6]提出一种基于后验校验对数似然比[6-8]的方法来对RS码进行识别，但需要在发射端和接收端预定义RS编码集。以上方法并未对缩短RS码进行识别，识别分析不够全面。

针对以上不足，本文提出一种基于非零均值比的盲识别算法来完成RS码和缩短RS码的识别。利用截获到的RS码序列建立分析矩阵，通过有限域的高斯约当算法[9]获得分析矩阵的非零均值比，以此来识别码长、符号数和本原多项式，然后通过伽罗华域傅里叶变换(Galois field Fourier transform，GFFT)来完成信息位长及生成多项式的识别，最后针对典型的RS码和缩短RS码编码方式，设计了仿真分析实验，对不同识别算法在不同误码率下的识别性能进行了分析比较。

1 RS码识别基础

RS码属于一个特殊的非二进制BCH码，码符号来源于伽罗华域(Galois field，GF)，GF(2m)，其中m表示每个符号的位数且m≥3。假设α为GF(2m)的本原元，则α2m-1=1。在纠错能力为t的(n,k)RS码中，α,α2,…α2t是 n-k次生成多项式 g(x)的根，则 g(x)为

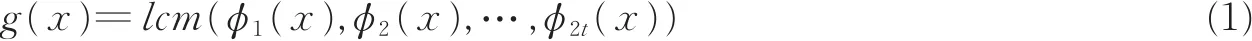
式中：φi(x)是 αi的最小多项式，由于 αi是 GF(2m)中的元素，φi(x)=x- αi，则 g(x)可以表示为[10]

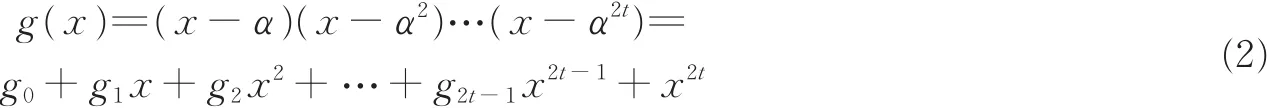
式中：g(x)有2t+1非零项，而g(x)是n-k次多项式，所以n-k=2t。

综上所述，需要识别的GF(2m)上的RS码参数分别为：

(1)码字长度n。其中本原RS码n=2m-1，而缩短RS码[11]是原(n,k)本原RS码删除前i位信息位为0的码字后所构造的新码，由于仍可构成一个(ki)维的线性子空间，所以能得到一个(n-i,ki)(1≤ i≤ k)的缩短RS码，其码长n≠ 2m-1，其他参数均与原RS码相同，识别方法基本与本原RS码一致。

(2)信息位长k=n-2t。

(3)校验位长2t=n-k。

(4)生成多项式g(x)。

(5)符号数m，一般m取3～8。

(6)本原多项式p(x)，一般采用十进制表示，如p=41表示 p(x)=x5+x3+1，因为4110=1010012。符号数m及其本原多项式如表1所示[12]。

表1 m值及其对应的本原多项式十进制表示Tab.1 m and decimal primitive polynomial

2 基于非零均值比的盲识别算法

在实际通信系统中，(n,k,m,p)RS码是以二进制等价码流进行传输的[13]，所以需先将截获得到的RS码序列转化为GF(2m)码元，并构建分析矩阵，通过有限域的高斯约当算法[9]获得分析矩阵的非零均值比，以此来识别码长、符号数和本原多项式，最后通过GFFT来完成信息位长及生成多项式的识别。

2.1 基于非零均值比的码长、符号数和本原多项式的识别

利用假定的符号数m′及本原多项式p′将截获到的RS码流转化为GF(2m)上的0～2m元素，按行放入一个a×b的矩阵A中，其中a表示矩阵的行数，b表示矩阵的列数，且a≫b。如果矩阵A的矩阵列数为真实码长且符号数及本原多项式估计正确时，则每行的信息位和校验位对齐，由于校验码元与信息码元线性相关，每行均存在着相同的线性关系，当对矩阵A进行高斯消元变换后，n-k列相关列（校验位所在的列）将会被消去，只会留下k列非零列即独立列（信息位所在的列），如图1(a)所示，分析矩阵将会出现秩的缺失；反之，当列数不是真实码长或符号数及本原多项式估计错误时，同一码字的信息位和奇偶校验位在不同的行中被隔离，在同一列中没有正确对齐，校验位不能被表示为信息位的线性组合，在特定的行中线性关系将受到影响，而这将导致列之间的线性关系消失，因此，矩阵A会表现得像一个随机矩阵。当矩阵A进行高斯消元变换后，由于不存在相关列，所以秩被完全获得，如图1(b)所示，则分析矩阵为满秩矩阵。

简而言之 ，当且 仅当m′=mest,p′=pest,b=nest时，矩阵A为秩缺矩阵，在无误码的情况下计算矩阵秩ρ如式(3)所示，归一化秩ρ′如式(4)所示，此时，秩ρ等于信息位长，归一化秩ρ′为码率r。

图1 分析矩阵结构图Fig.1 Structure of analysis matrix

其他情况下，矩阵A为满秩矩阵，此时矩阵秩ρ如式(5)所示，归一化秩ρ′如式(6)所示，此时，秩ρ等于列数，归一化秩ρ′为1。

在无误码的情况下，可利用有限域的高斯约当法对矩阵A求秩来识别码长、符号数及本原多项式，当且仅当归一化秩ρ′最小时完成识别。然而在有误码的情况下，直接求秩法并不适用[5，9，14]。如前所述，当一个矩阵所有行和列都是线性无关的，此时称为满秩矩阵；如果一个矩阵至少有一列/行依赖于其他列/行，那么此时会出现秩缺。在实际通信系统中，传输错误或白噪声的存在增加了行/列之间的线性无关性[15]，并且这种线性无关随着噪声强度的增大而增大，当噪声水平超过阈值时，使分析矩阵A不会有任何相关列/行，就像一个随机矩阵。此时，不管列数b是否等于真实码长，矩阵A均会是一个满秩矩阵。

但在有误码的情况下，利用有限域的高斯约当算法将矩阵A转换成为三角矩阵Q，通过对下三角阵Q的观察可以发现，与独立列相比，相关列的非零元素较少，因此，存在秩缺失的矩阵比满秩矩阵含有的零元素要少，因此，在有误码的情况下，可以根据矩阵Q中每列的非零元素所占的比例来确定矩阵的秩缺情况，故定义非零均值比u′(b)来表示矩阵的秩缺失情况为

式中：φ′(c)表示第c列中非零的数目，φ′(c)表示下三角矩阵Q中第c列含非零数目所占比重。

利用有限域的高斯约当消元法将分析矩阵A转化为下三角阵Q后，通过计算矩阵Q的非零均值比u′(b)来完成 RS码参数的盲识别，当且仅当 m′=mest,p′=pest,b=nest时，u′(b)最小。

2.2 信息位、校验位及生成多项式的识别

设GF(2m)上的多项式[16]

则它在GF(q)的谱多项式为

在RS码中，码多项式与生成多项式具有相同的码根，因此，在码长，符号数及本原多项式正确识别后，将接受序列按正确码长分组对其进行GFFT变换，并采用最大似然法来评估根数，当多组码字经GFFT后具有相同的连零位置且个数相同时，由此可以估计出码根数即校验位长2t，通过计算n-2t=k即可求取信息位长，最后通过式（2）得到生成多项式g(x)。

2.3 算法流程

（1）设RS码的估计码长为n′，遍历对应的符号数m′及本原多项式p′，并利用p′将截获的RS码序列由GF(2)转化为GF(2m)中的元素。

（2）将转化后的RS码序列按行放入a×b的矩阵A中，其中a为矩阵的行数，b为矩阵的列数，b=n′且满足a≫b，构建分析矩阵。

（3）利用有限域的高斯消元法将A转化为下三角阵Q。

（4）计算每列列中非零的数目φ′(c)，并计算出每列非零数目所占比重φ′(c)。

（5）计算整个下三角阵Q的非零均值比u′(b)。

（6）改变 RS 的估计码长 n′，重复步骤（1）—（5），当且仅当非零均值比 u′(b)最小时完成识别，即

（7）计算码字多项式的根，记录根的数目来估计n-k，从而计算出信息位长k。

（8）根据式(2)计算生成多项式g(x)。

3 仿真实验与性能分析

3.1 实验仿真

为了验证本文所提方法的有效性，分别针对本原RS码以及缩短RS码设计仿真分析实验，编码参数设置如表2所示。利用MATLAB随机生成0、1随机序列，然后以表2中编码参数进行编码，并叠加高斯随机噪声，信噪比SNR=10dB，产生误码率为pe=0.01的码序列，并用本文所提出的算法对其进行识别。

表2 参数设置Tab.2 Parameter setting

从图2可以看出，与其他可能的组合相比，当[n,m,p]=[63,6,103]时，u′(b)达到最小值，因此，可以识别出码长，符号数及本原多项式。当正确识别码长、符号数及本原多项式后，利用GFFT可以计算出在码根α5,α4,α3,α2,α处码谱为 0，码根数为 5，即校验位长 2t=5，则k=n-2t=58，即信息位长 58，将码根代入式（2），可以得到生成多项式g(x)=x5+62x4+32x3+53x2+3x+31。至此，完成了对本原RS码的识别。

同样地，在图3中，当[n,m,p]=[204,8,285]，u′(b)达到最小值，因此，可以识别出码长、符号数及本原多项式。当正确识别码长、符号数及本原多项式后，利用GFFT可以计算出在码根α5,α4,α3,α2,α处码谱为0，码根数为5，即校验位长2t=5，则k=n-2t=199，即信息位长199，将码根代入式（2），可以得到生成多项式g(x)=x5+62x4+63x3+229x2+197x+38。至此，完成了对缩短RS码的识别。

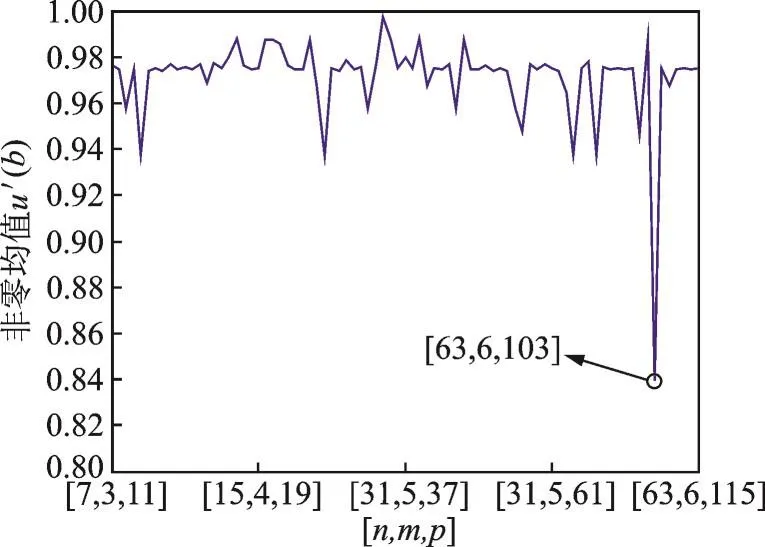
图2 本原RS码识别时u′(b)随估计参数的变化Fig.2 Values of assuming primitive RS code

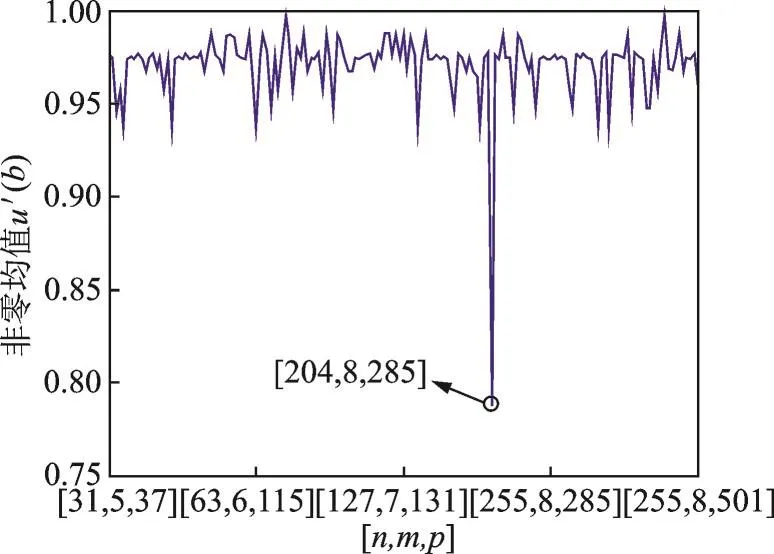
图3 缩短RS码识别时u′(b)随估计参数的变化Fig.3 Values of assuming short RS code

3.2 识别性能分析

在图4中，对n=15,m=4,p=19的RS码，选取k=7,k=9,k=11不同的信息位长在不同误码率的情况下进行识别性能分析，从图4中可以看出，RS码参数识别性能随着信息位长k或码率r的增大而减小。随着r的增大，n-k减小即相关列会随之减少，利用u′(b)区分满秩矩阵和秩缺矩阵难度加大，因此，识别难度加大，准确度下降。

在图5中，对码率r≈0.6的(63,38,6,67)RS码，(127,76,7,131)RS码和(255,153,8,285)RS码在不同误码率的情况下进行识别性能分析，从图5中可以看出，RS码参数识别性能随着码长n的增大而减小，在误码率不超过0.02时，对所有RS码都能达到90%的识别率，具有较好的识别性能。

图4 不同信息位长识别性能比较Fig.4 Comparison of recognition performance among different information bit lengths

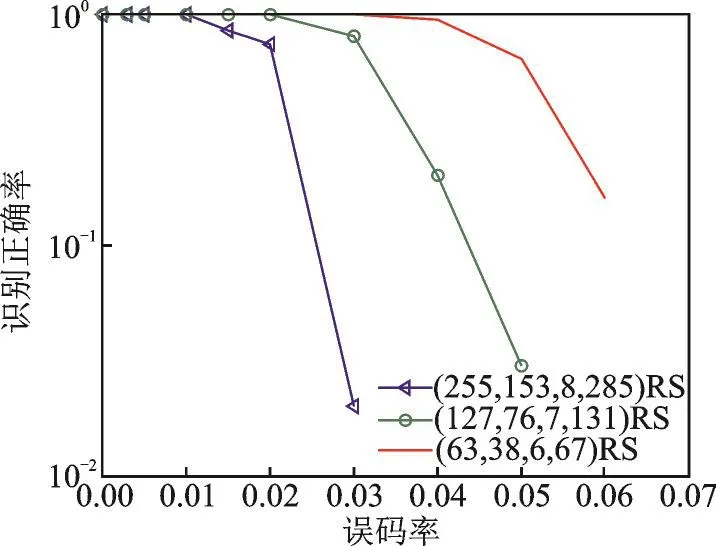
图5 不同码长识别性能比较Fig.5 Comparison of recognition performance among different code lengths

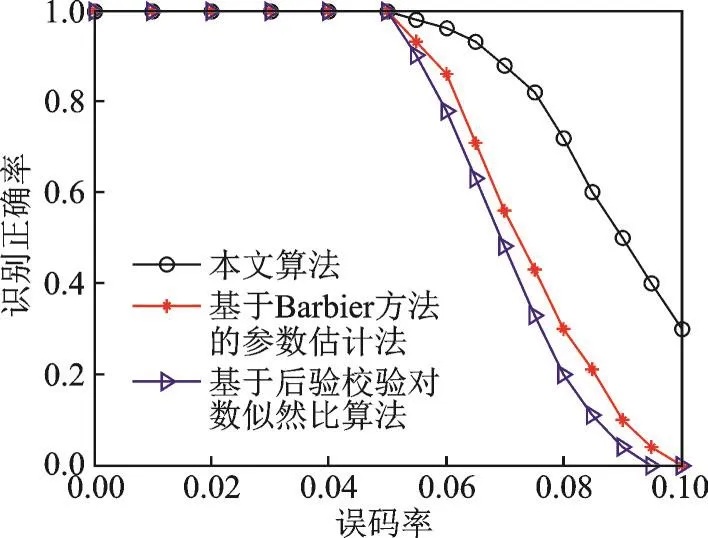
图6 3种算法识别性能比较Fig.6 Comparison of recognition performance among three algorithms

表3 不同算法的运行时间对比Tab.3 Comparison of run time among different algorithms

图6给出了在采用(15,7,4,19)RS码时，本文算法，文献[6]中基于后验校验对数似然比算法与文献[4]中基于Barbier方法的参数估计法的比较。随着误码率的增加，3种算法识别性能也随之下降，但本文算法下降较慢，优于其他两种算法，并给出了正确识别一次3种算法所需时间，如表3所示，本文算法运算时间由于经过多次行列变换，稍逊于基于后验校验对数似然比算法，但抗误码性能较优。

4 结束语

根据RS码的编码结构及特点，提出了一种基于非零均值比的RS码盲识别方法，利用有限域的高斯消元法计算出分析矩阵的非零均值比来确定码长、符号数及本原多项式，然后利用GFFT变换求解出其他参数，完成了对本原RS码缩短RS码的识别，并且分析了信息位长和码长与识别的准确性之间的关系，随着信息位长和码长度的减少，识别更加准确。并与文献[4，6]方法进行比较，本文算法抗误码性能优于其他两种算法，并且计算复杂度低，更适合有噪环境下的RS码识别。