利用部分采样的数字混合信号单通道盲分离算法

马 欢 郭 勇 吴广恩 闵 刚 张长青

（国防科技大学信息通信学院，西安，710106）

引 言

随着通信需求的不断增加，具有更高频谱利用效率的新型通信方式被提出，例如成对载波多址（Paired-carrier multiple access,PCMA），以其较高的频谱利用效率和较好的抗截获能力，在合作化军事通信领域得到运用。在通信侦察中，PCMA信号时频域均发生混叠，传统的信号分析方法不再适用，近年来基于单通道盲分离思想的混合信号处理方法是分析该类信号的主流算法[1]。单通道盲分离是指仅根据单路混合信号观测值实现多个时频混叠信号分量的分离。目前对于数字通信混合信号的单通道盲分离主要有基于Viterbi思想的逐留存路径处理(Per-survivor processing,PSP)[2-3]盲分离算法和基于粒子滤波(Particle filtering)的盲分离算法[4-6]。PSP算法具有复杂度低、对信道跟踪速度快等优点，其缺点是对信道参数的初始设置较为敏感，容易陷入局部极小点，且无法应用至符号速率不同情况下的盲分离。粒子滤波盲分离算法具有对各分量信号调制参数无特殊要求，可综合利用多个参数差异，以及适用于符号速率不同情况下的盲分离[4]等优点，但其最大的缺点是复杂度太高。

文献[7]基于贝叶斯递推估计思想，通过对混合信号中的发送符号序列和信道参数进行联合估计，实现了数字通信混合信号的单通道盲分离。文献[8]在文献[7]的基础上重新对混合信号的调制参数进行建模，改进调制参数粒子采样分布，改善采样效率，算法性能进一步提升。由于受到发送端成型脉冲拖尾以及信道的影响，接收端的等效信道往往具有记忆性，当前时刻的观测值可以为之前时刻的符号估计提供重要信息[9-10]。传统粒子滤波盲分离算法在符号粒子采样过程中引入了平滑处理，利用观测值yk-D:k辅助产生k-D时刻的符号粒子，D为平滑长度。采用平滑处理后，分离性能得到了很大提升。然而传统平滑算法在完成粒子采样和权重更新时需要对k-D时刻至k时刻的D+1个观测值进行波形重构[8]，算法的搜索状态空间数与平滑长度成指数倍关系增长，运算复杂度非常高。当采用较大平滑长度时，对于调制阶数较高的混合信号，计算机无法处理。因此，研究降低算法复杂度至关重要。

针对该问题，本文从降低粒子采样和权值更新过程中所需搜索的状态空间数出发，提出了两种新的采样方法：部分采样法和混合采样法。前者通过产生若干组序列，使用这些序列代替对平滑区间内的所有状态空间进行搜索，利用每组序列的增量权重完成粒子采样和权值更新。后者将平滑区间分为两部分，第一部分采用传统的全状态空间法进行搜索，第二部分采用部分采样法进行搜索，最后利用两个子区间的总增量权重完成粒子抽样和权重更新，实现降低算法复杂度的目的。

1 粒子滤波盲分离算法及复杂度分析

1.1 信号模型

为不失一般性，假设两路同频（或近似同频）多进制数字相位调制(Multiple phase shift keying，MPSK)信号混合的情况。为简化分析，假设混合信号中各分量信号具有相同的符号周期T，并对接收信号以符号速率采样，则其复基带模型可以表示为

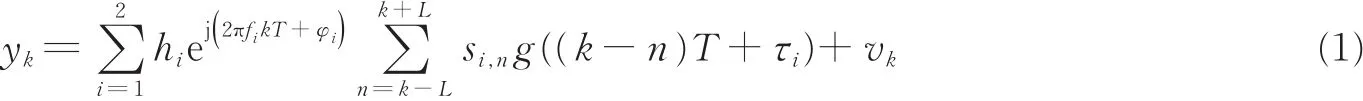
式中：幅度hi、频偏fi、初始相位φi、相对时延τi和第n个发送符号si,n为第i路源信号的调制参数，i=1,2；g为发送端成型滤波器；L表示其拖尾长度；vk表示方差为的高斯白噪声。

根据贝叶斯理论，单通道盲分离就是利用后验分布p(s1,1:k,s2,1:k,Θk|y1:k)，Θk={hi,k,fi,k,φi,k,τi,k}，迭代估计两路源信号的发送符号。受发送端成型脉冲的影响，可采用平滑的方法[5]，即估计后验分布为平滑长度，限定0＜D≤2L。假设混合信号的调制参数集Θk在一个信号帧长度内是不变的，单通道盲分离问题的动态系统模型可表示为

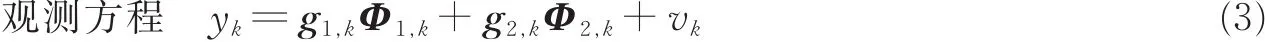
1.2 粒子滤波盲分离算法

得到观测序列y1:k后，需要对后验分布p(Φk-D,Θk|y1:k)进行递推求解。文献[7]基于贝叶斯思想，利用粒子集作为后验分布的估计，其中w(j)为权重，N为粒子总数。算法选择抽样函k数为

权重更新公式为

由于参数Θ的迭代与符号Φ的取值无关，式(4)进一步分解为

抽样分为两步，第一步根据p(Θk|Θk-1)抽取k时刻的参数粒子，可以采用核平滑方法[8]。第二步根据抽样得到符号粒子

参数Θk的最小均方误差估计值为

粒子滤波盲分离算法流程如算法1所示。

算法1粒子滤波盲分离算法

（5）重采样threshold重采样end；

（6）符号估计：根据式(8)和式(9)分别得到符号和参数的估计值；

（7）k=k+1，转至步骤（2）。

本文旨在降低粒子滤波盲分离算法中符号粒子采样和权值更新过程中的计算复杂度，为表述清晰，下文的复杂度分析和新算法介绍均不再提及参数粒子的更新和计算。

1.3 复杂度分析

传统粒子滤波盲分离算法中，需要计算式(7)和式(5)，但两者的直接计算较为困难，其近似数值计算公式为[4]

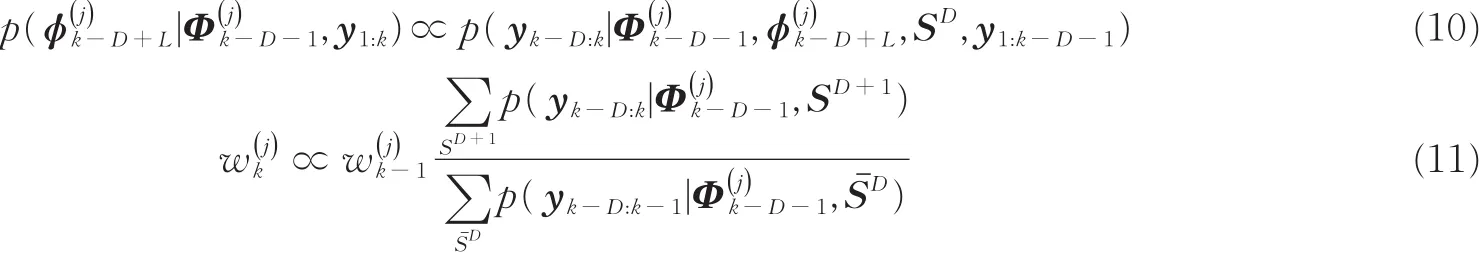
式(10,11)的数值计算关键在于计算其中的求和式。容易看出式(10,11)分母的计算包含于式(11)分子的计算过程中，以式(11)分子的计算为例来分析算法的计算复杂度。基于观测噪声的独立不相关特性，有

φk+L-j从 SD+1中取值。k时刻的似然函数，可表示为

式(12)的数值分析需对SD+1进行搜索。例如图1所示的搜索空间树，图中平滑长度D=2，圆点表示空间符号，线段表示符号更新，横轴代表时间。符号粒子位于初始时刻，搜索空间依照SD+1转移至k。注意到该树内k时刻之前所有状态的搜索计算已在之前时刻符号粒子的抽样过程中完成，因此，完成k时刻符号粒子的抽样，只需搜索计算图1所示的树在k时刻的所有状态。对于两路MPSK混合信号，每时刻符号对φk的取值有|M|2种可能，|M|为单路MPSK信号的星座点数。容易看出，图1所示的树在k时刻有|M|2()D+1种状态。因此,计算式(12)所需要搜索的状态空间数为|M|2()D+1。

可知随着D的增大，算法每时刻需搜索的状态空间数指数级增加，其计算复杂度为

图1 用于计算式(12)的树Fig.1 The tree used for computing Eq.(12)

本文通过合理丢弃不必要的搜索空间以期降低算法复杂度。

2 低复杂度符号粒子采样法

2.1 部分采样法

从前文的分析可以看出，如果能够按照某种方式合理地丢弃一些搜索空间，而仅保留对采样贡献较大的搜索空间，便可实现计算复杂度与性能之间的折中。

基于上述设想，本文给出一种部分采样法(Partial sampling)。对于两路MPSK信号混合，k-D时刻种状态，初始化|M|2组序列，分别以φk-D+L=λi（λi∈A，A为等效符号空间，即λi=(s,s)，s,s∈ M，m,n=1,…,|M|）开始，下面给出 φ= λ这组的采样方法：基于构

1,m2,n1,m2,nk-D+Li建计算其增量权重时刻每个可能的符号对取值λl∈A， 基 于构 建，按照此法获得|M|2个不同，利用其采样得到并计算对应的增量权重 γ同理更新至k时刻，得到和权重最终可以得到|M|2个总的增量权重，用其作为k-D时刻的符号采样分布，完成采样。图2给出了D=2时的算法示意图，图中实线代表保留，虚线代表丢弃。算法流程如算法2所示。

图2 部分采样流程示意图Fig.2 Illustration of partial sampling

算法2部分采样算法

end

（2）复杂度分析

2.2 混合采样法

更进一步，综合部分采样法和传统采样法的优势，将搜索空间划分为D1和D2两部分，D=D1+D2，分别利用传统方法和部分采样法完成搜索，称之为混合采样法(Hybrid sampling)。如图3所示，D1=1，D2=3，D=4。粗线和细线分别代表传统方法和部分采样法。算法流程如算法3所示。

算法3混合采样方法

forj=1:N

forλi∈ A

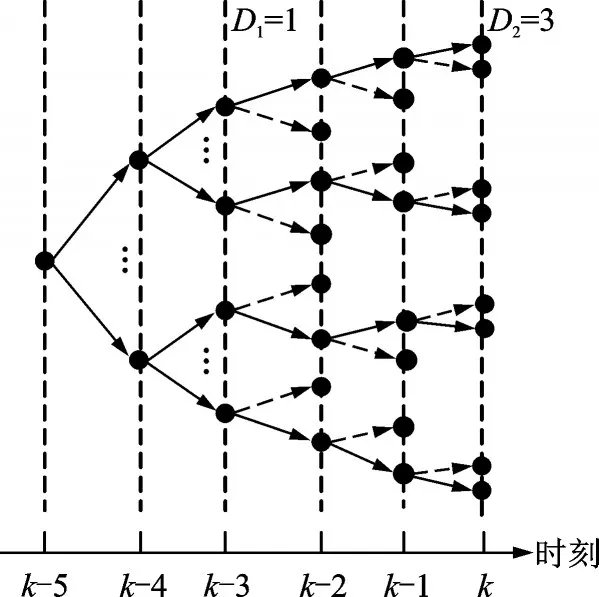
图3 混合采样方法采样流程示意图Fig.3 Illustration of hybrid sampling

end

end

forλi∈ A

依照式(24)计算 ρ(i,j)k-D；

end

权重计算：依照式(25)进行；

end

以下对混合采样法作几点说明:

证明：假设有 Φk-D上的可测函数 h(·)，定义其在 Φk上的拓展函数为 h*(·)，有 h*h(Φk-D)。设c为常数，且使式(26)左右相等，那么c在 SˉD1内均为常数，根据

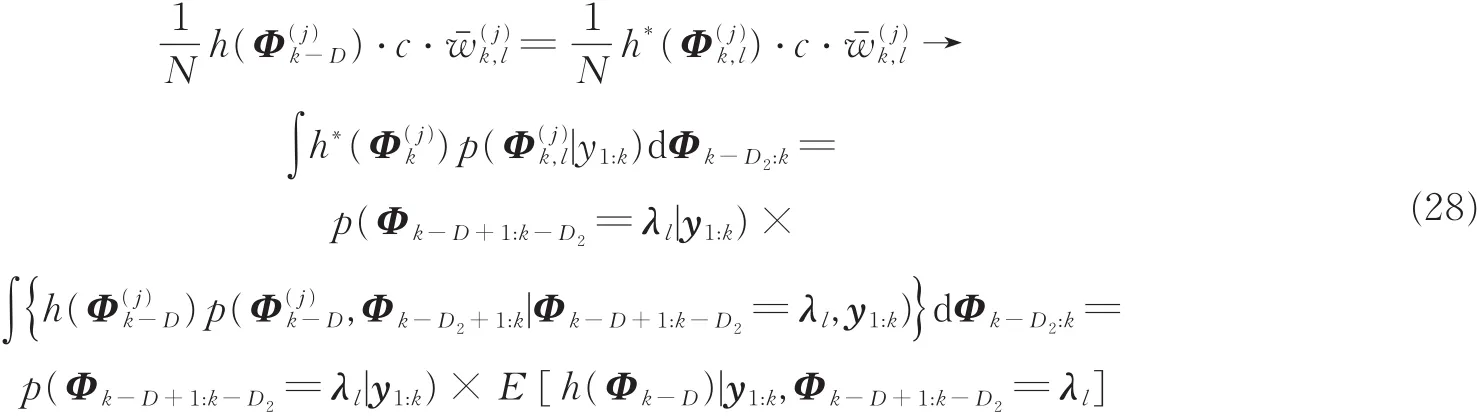
因此

按照粒子滤波理论[5]，，证毕。

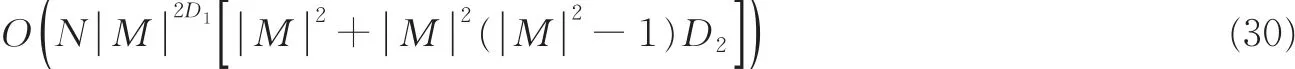
3 实验仿真

考虑两路BPSK调制信号的混合，仿真参数为：h1=1，h2=0.8；τ1=0.1T，τ2=0.3T；φ1=0，φ2=π/3；T=1× 10-5s；f1=0.02kHz，f2=0.04kHz；L=4，成型滤波器滚降因子α=0.3，N=100；算法性能由平均误符号率体现。

首先在不同D的情况下，对传统方法和部分采样法的搜索空间数进行了对比，结果如表1所示。随着D的增大，前者搜索空间数急剧增大，而后者不明显。例如D=4时，两者之比为20∶1。图4给出了二者的性能曲线，可见随着D的增大，二者性能均得到了提升。

表1 传统采样法和部分采样法在不同平滑长度下的搜索空间数Tab.1 Searching spaces of traditional and partial sampling methods at different smoothing lengths

图4 传统采样法和部分采样法在不同平滑长度下的性能曲线Fig.4 SER performance of traditional and partial sampling methods at different smoothing lengths

表2给出了D=4，D1和D2取值不同时，混合采样法的搜索空间数。可以看出，其搜索空间数介于前两者之间。图5给出了性能曲线。由图5可知，和部分采样法相比，其性能有明显改善；与传统算法相比，在降低复杂度的同时其性能损失不明显，例如，D1=2,D2=2时，性能损失不超过0.3dB。

表2 混合采样法搜索空间数Tab.2 Searching spaces of hybrid sampling method

图6给出了不同频偏下的性能曲线，仿真中令f1=ΔxkHz，f2=-ΔxkHz。可看出，当Δx增大时，混合信号的调制参数差异变得明显，算法性能均得到了提升[4]。但一味的增大Δx，性能并不会一直改善，这是因为性能仍受到其他因素的影响，不可能无限制的提升[4]。此外本文提出的两种算法对频偏均不敏感。图7考察了不同相对时延下的算法性能。仿真中令τ1=0.1，τ2=Δx×T。可以看出，同样随着时延差的增大，算法性能得到提升，这是因为随着时延差增大，混合信号调制参数差异变得明显，更易于实现分离；但超过0.5后，性能恶化，此时第二路信号码间串扰严重，误符号率增加，导致总体性能下降。

图5 混合采样法性能曲线图Fig.5 SER performance of hybrid sampling method

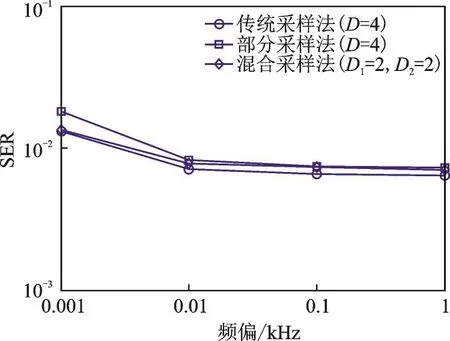
图6 不同频偏下算法性能曲线(SNR=12dB)Fig.6 SER performance under different frequency offsets(SNR=12dB)

图7 不同时延下算法性能曲线(SNR=12dB)Fig.7 SER performance under different time delays(SNR=12dB)

4 结束语

基于粒子滤波的盲分离算法在数字混合信号单通道盲分离应用中发挥了重大作用，但复杂度太高是其一大缺陷。通过深入分析算法的数值计算过程，得出复杂度高的主要原因为粒子采样和权值更新过程中搜索空间数与平滑长度成指数倍关系增长。提出按照一定方式合理的丢弃部分对采样和权重计算贡献度不大的搜索空间，降低复杂度，形成了两种采样方法：部分采样法和混合采样法。理论分析和仿真验证均表明，本文算法在降低复杂度的同时性能损失不明显，是一种有效的低复杂度盲分离算法。