基于ABAQUS的喷雾机喷杆结构拓扑优化

乔白羽，丁素明，薛新宇，崔龙飞，顾 伟，陈 晨

(农业部南京农业机械化研究所，南京 210014)

0 引言

近年来，随着中国农业机械化进程的加速推进，大型植保机械得到了快速的发展，地面植保机具中，大型喷杆喷雾机应用最为广泛，主要使用在大田作业中[1-5]。大型喷杆喷雾机的优点是作业效率高、施药面积大，能够极大程度地减小作业过程中对农作物的损害，因此具有较大的使用价值。但是，大型喷杆喷雾机在田间施药的过程中，由于地面不平所产生的外部激励会通过机架传递到喷杆，导致喷杆发生振动，进而影响到喷雾效率，降低药液的分布均匀性，严重时还会引起喷杆的断裂，从而降低喷雾效率，缩短喷杆喷雾机的使用寿命[6-9]。

为了减轻喷雾机喷杆的振动，提高喷杆喷雾机在田间作业过程中的喷洒效率，国内外学者在机械结构抑振方面进行了大量的研究。其中，Rong J.H.等人基于约束频率和约束响应之间的函数关系式，利用结构拓扑优化方法，对机械结构进行了拓扑优化研究，证明了拓扑优化对机械结构的抑振性能[10]；Niordson等人对梁结构进行了结构优化设计，结果显示优化后梁结构的抗振性能极大的提高[11]；李艳辉等以钢架结构作为研究对象，将钢架结构的固有频率作为目标函数，利用结构节点渐进法对其进行了动力学性能优化[12]；陈晨等人研究了喷杆的动力学特性以及结构尺寸优化，结果表明构成喷杆的钢管壁厚和截面尺寸均与喷杆的1阶固有频率成正比，为喷杆的进一步动力学性能研究以及结构优化做准备[13]；茅志颖等人对结构优化设计的渐进优化理论进行了研究，提出了基于渐近理论的结构性能优化方法，并通过试验验证了多目标多约束优化方法的合理性[14]；扶原放等基于变密度法对某微型电动车的车架结构进行了拓扑优化设计，优化结果显示优化后车架结构的动力学性能得到很大提升，并且实现了车架结构的轻量化设计[15]；陈达等以等腰梯形的喷杆悬架结构为研究对象对其进行了优化设计，采用动态测试分析、有限元模态分析及整机路谱模拟等方法，优化了悬架结构的动力学性能，减轻了悬架结构的振动[16]。

上述将拓扑优化方法应用到其他机械结构中已经实现了部分机械结构的动力学性能优化，但并没有从机械结构的原始设计方面考虑，也没有将拓扑优化方法应用到喷杆结构的优化设计中。为此，基于计算机辅助优化设计的设计理论与方法，从喷杆原始设计出发，通过改变喷杆结构的内部材料布局，对喷杆进行最优拓扑优化，从而实现减振的目的。

1 喷杆的结构设计

本文利用三维建模软件Pro/E建立了喷杆喷雾机的几何模型，如图1所示。此次研究的喷杆主要由方形钢管和圆柱形钢管焊接而成的5段式喷杆，整个喷杆总长为12m。其中，每侧喷杆的两段喷杆之间以回转关节的方式折叠放置，机架与喷杆直接相连，是振动传递的主要来源。整个机身主要包括4根方形钢管、6根圆柱形钢管、药箱、连接部件，以及其他辅助构件。此次拓扑优化不考虑药箱和喷头的作用，在优化过程中只对喷杆和机架部分进行拓扑优化。由图1可以看到，目前喷杆的内部分布多为四边形，此种结构形状不稳定，不利于减轻喷杆作业过程中所产生的振动，所以需要对喷杆的内部材料分布进行优化，以达到最好的材料布局，从而提高喷杆的动力学性能。

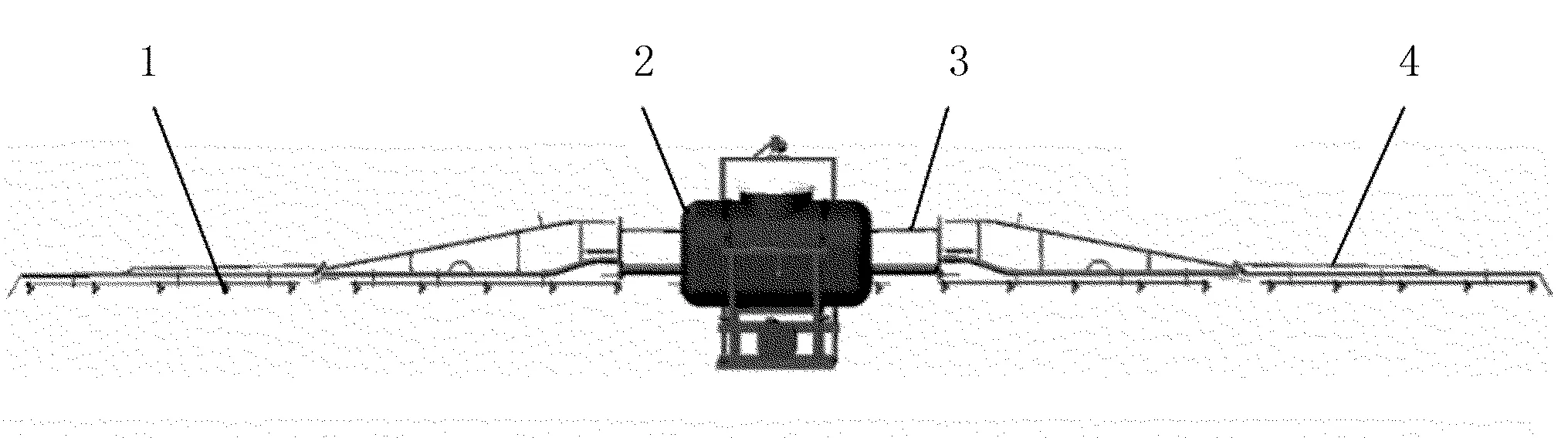
1.喷头 2.药箱 3.机架 4.喷杆

2 喷杆结构的拓扑优化

2.1 拓扑优化理论基础

拓扑优化技术已经广泛应用于机械结构的优化设计中，这种方法的优点就是可以在结构的初始设计过程中，使得材料得到合理分配，从而减轻机械结构的重量[17-19]。将拓扑优化技术应用于喷杆的结构设计中，不仅可以缩短喷杆的制造时间，还可以提高喷杆的结构性能。

拓扑优化的基本思想是在指定的区域内寻求材料的最佳布局。通过设置目标函数和约束条件，对设计域内的单元进行取舍，实现结构在指定约束条件下的最优设计。目前，机械结构拓扑优化的方法主要有均匀化法、变密度法、渐进结构优化法以及变厚度法[20]。本文采用的是变密度法对喷杆结构进行拓扑优化求解。变密度法的基本原理：假想一种密度可变的材料，人为的去设定材料的物理参数特性与密度之间的关系，在拓扑优化过程中将材料的密度定义为拓扑优化的设计变量，从而将拓扑优化的问题转变成材料最优分布的问题，实现材料的最合理分布，从而实现最优拓扑结构[21]。

拓扑优化的数学模型为

Minf(x)

s.t.gj(x)≤0j=1,…,m

hk(x)=0k=1,…,n

X=(x1,x2,…,xn)

0≤xi≤1i=1,…,r

式中x—单元密度；

f(x)—目标函数；

g(x) —不等式约束函数；

h(x)—等式约束函数。

结构拓扑优化的3个重要因素就是设计变量、约束函数以及目标函数，拓扑优化的具体过程是：在设置好设计变量和约束函数后，通过对其进行迭代，实现目标函数最优的过程。拓扑优化的本质就是材料最优分布问题，也就是通过拓扑优化去除不必要的材料，将材料添加到结构性能需要加强的区域，通过寻找合理的载荷传递路径，提高材料的使用效率，提升结构的刚度和模态性能[22-23]。

2.2 拓扑优化模型的建立

在进行结构拓扑优化之前，首先需要根据实际要求建立结构的初始拓扑优化模型，初始结构模型可以分为实体单元或者壳单元，通过简化结构的设计域和非设计域来控制结构的拓扑优化设计。由于此次研究的喷杆结构具有对称结构，因此只需要对喷杆的右侧进行拓扑优化即可。优化之前，所建立的喷杆结构模型为2 260×500的长方形模型，单元类型为壳单元，如图2所示。

图2 拓扑分析模型的初始结构

上述的拓扑优化初始模型采用一阶四面体单元建立，设计域是整个拓扑优化分析模型。拓扑优化的单元尺寸为20mm，壳单元数量为2 850个，材料的特性定义如表1所示。

表1 初始模型的材料特性

2.3 拓扑优化的过程

2.3.1 确定设计变量、约束条件和目标函数

本次拓扑优化采用变密度法，思想和前提是：①将离散单元的相对密度定义为拓扑优化的设计变量，单元内部的其他材料属性均为常数；②在拓扑优化过程中，单元相对密度一直在变化，由此使得单元材料属性也在变化。基于上述两个前提和假设，材料的属性可以理解为初始材料的属性和单元相对密度之间的指数关系，且每一个单元只将密度作为唯一的设计变量，这样可以大大地简化拓扑优化的过程[24]。

根据上述分析，以调整喷杆的固有频率避开外界激励力的频率为主要目标，在不会大幅影响喷杆整体结构重量的前提下建立喷杆的优化模型。一般的喷杆喷雾机在田间作业时，会受到田间路面凹凸不平和喷雾机轮胎弹性的影响，导致喷雾机的机架受到激励，从而传递到喷杆，引起喷杆的振动，激励频率为0～10Hz[25-26]。因此，在定义拓扑优化的设计变量时，需要考虑喷雾机动态性能的要求，并结合优化设计理论来进行确定。

此次优化的边界条件是在初始模型的末端施加100N的力，力的大小是由右侧喷杆的质量所决定的，这样可以模拟喷杆的实际受力情况。本次拓扑优化的设计目标是畸变能密度最小，约束条件是体积减小初始体积的50%，位移约束等于或者小于0.001，这样可以保证拓扑优化的材料分布实现最佳布局。因此，拓扑优化的目标函数是在满足结构约束的条件下，最小化整个喷杆结构的畸变能，约束函数是在给定载荷约束和满足最小畸变能的条件下，实现喷杆结构的整体体积比。拓扑优化的数学模型为

minF(ηi)

式中F—结构的畸变能密度；

ηi—第i个单元的伪密度；

a—体积减小的百分比；

V0—喷杆的初始体积。

2.3.2 优化结果分析

完成上述步骤后，就可以进行迭代优化。本次拓扑优化在ABAQUS中进行，将喷杆初始模型的壳单元导入ABAQUS后，定义各个参数化变量，随后进入优化过程。本次优化一共进行31次迭代，优化后的密度和位移云图如图3和图4所示。

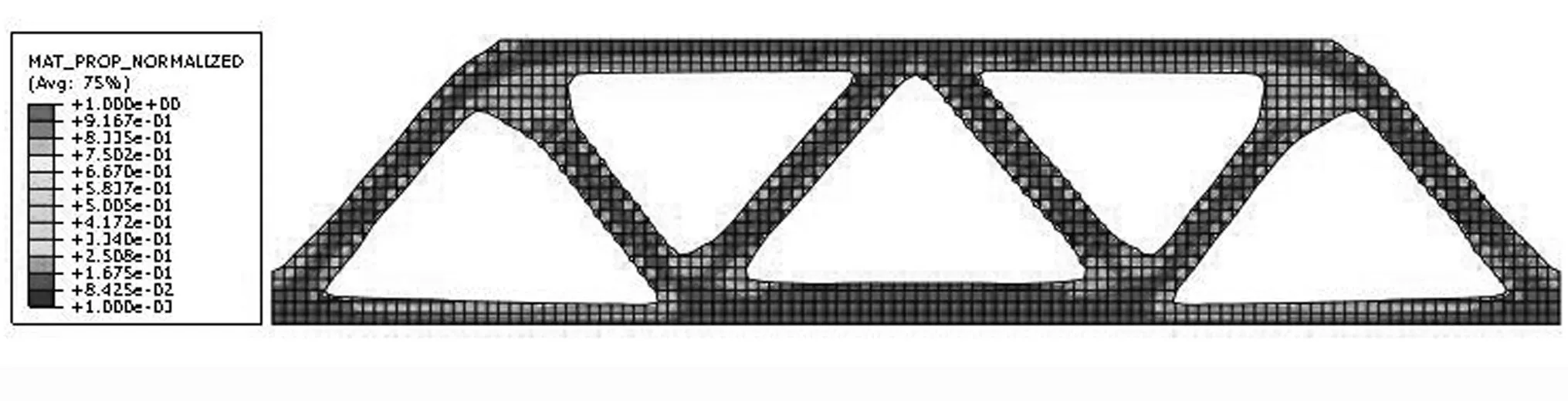
图3 拓扑优化后的密度云图

图4 拓扑优化后的位移云图

本次优化采用变密度法，可以看出，拓扑优化后的材料分布用单元密度值(0～1)来表示，图中的空洞部分表示密度值为0的部分，也就是拓扑优化后需要移除的材料。从图3、图4中可以看出：喷杆结构的最大变形量减少10.9%，最大应力减小27.6%，拓扑优化取得了很好的效果。

优化过程中的目标函数变化曲线如图5所示。它反映了在迭代过程中喷杆结构变形量的变化情况，随着迭代次数的增加，结构变形量在不断减小。约束函数变化曲线如图6所示。由图6可看出：随着迭代过程的进行，体积在不断减小，当体积减小到0.297m3时，总体积减小到初始体积的70%。

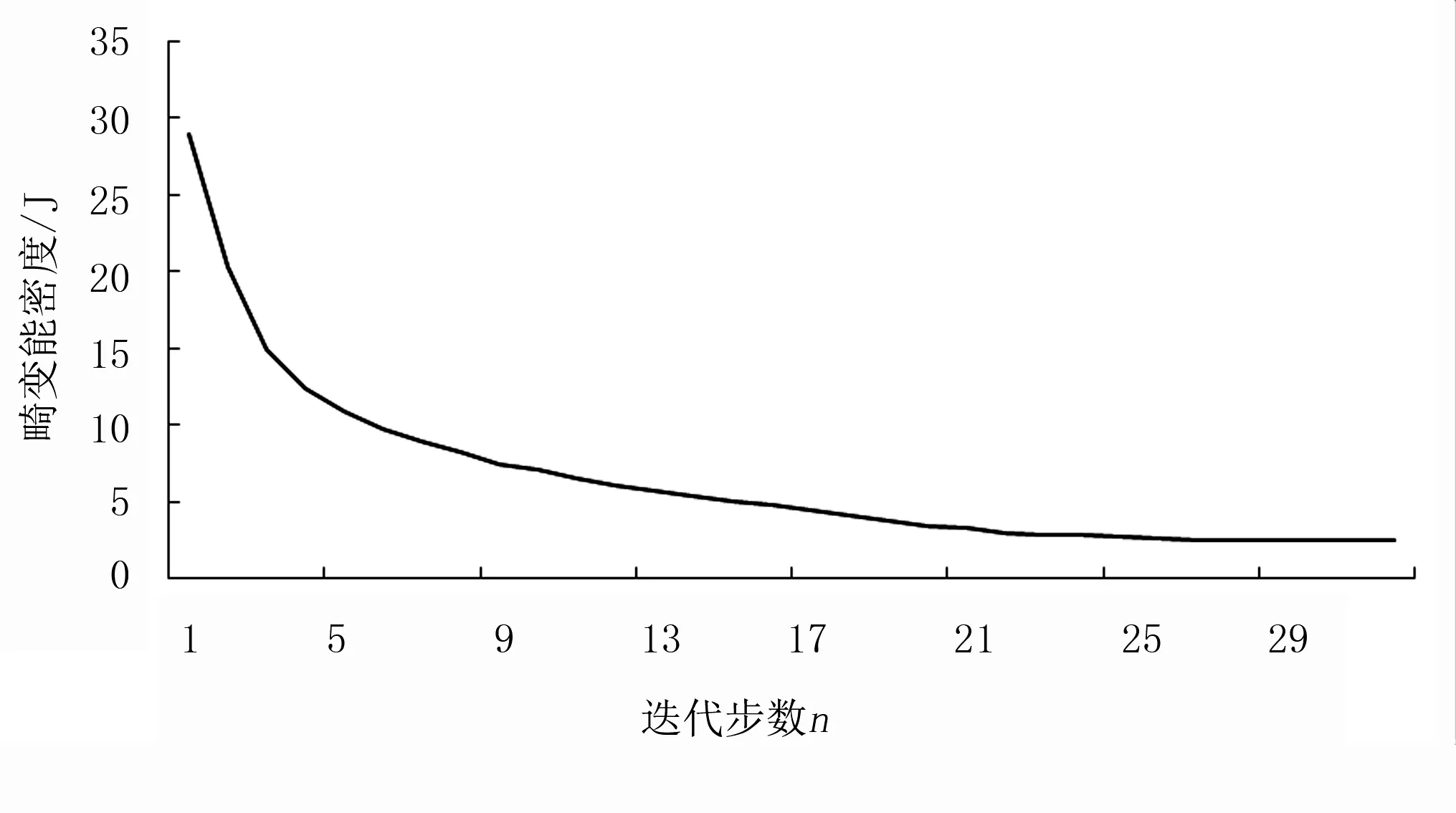
图5 结构变形量变化图

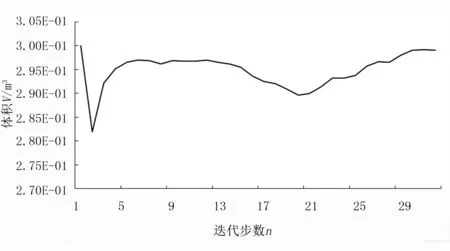
图6 体积变化图

3 优化后多段式喷杆的动态特性分析

根据上述分析，本次优化的主要目标是调整喷杆的固有频率使其避开外界的激励频率，同时在不大幅度改变喷杆质量的前提下建立喷杆的优化模型。 优化后的动力学特性分析就是为了比较喷杆在优化前后动力学特性的变化。通过将优化后的模型导入ABAQUS中，可以计算出优化后喷杆的前8阶固有频率和动力学性能。优化后喷杆材料的内部布局如图7所示。

图7 优化后喷杆内部材料分布

对优化后的整机喷杆进行动力学特性分析，获得优化前后前8阶多段式喷杆的阵型位移对比图，如图8所示。从图8可以看出：优化后喷杆的第1阶模态位移变形量由7.6mm下降到5.1mm；第2阶阶模态位移变形量由7mm下降到4.9mm，实现了低阶模态振动的有效控制，显著的减轻了喷杆的振动，进而改善了整个喷杆喷雾机的振动特性。

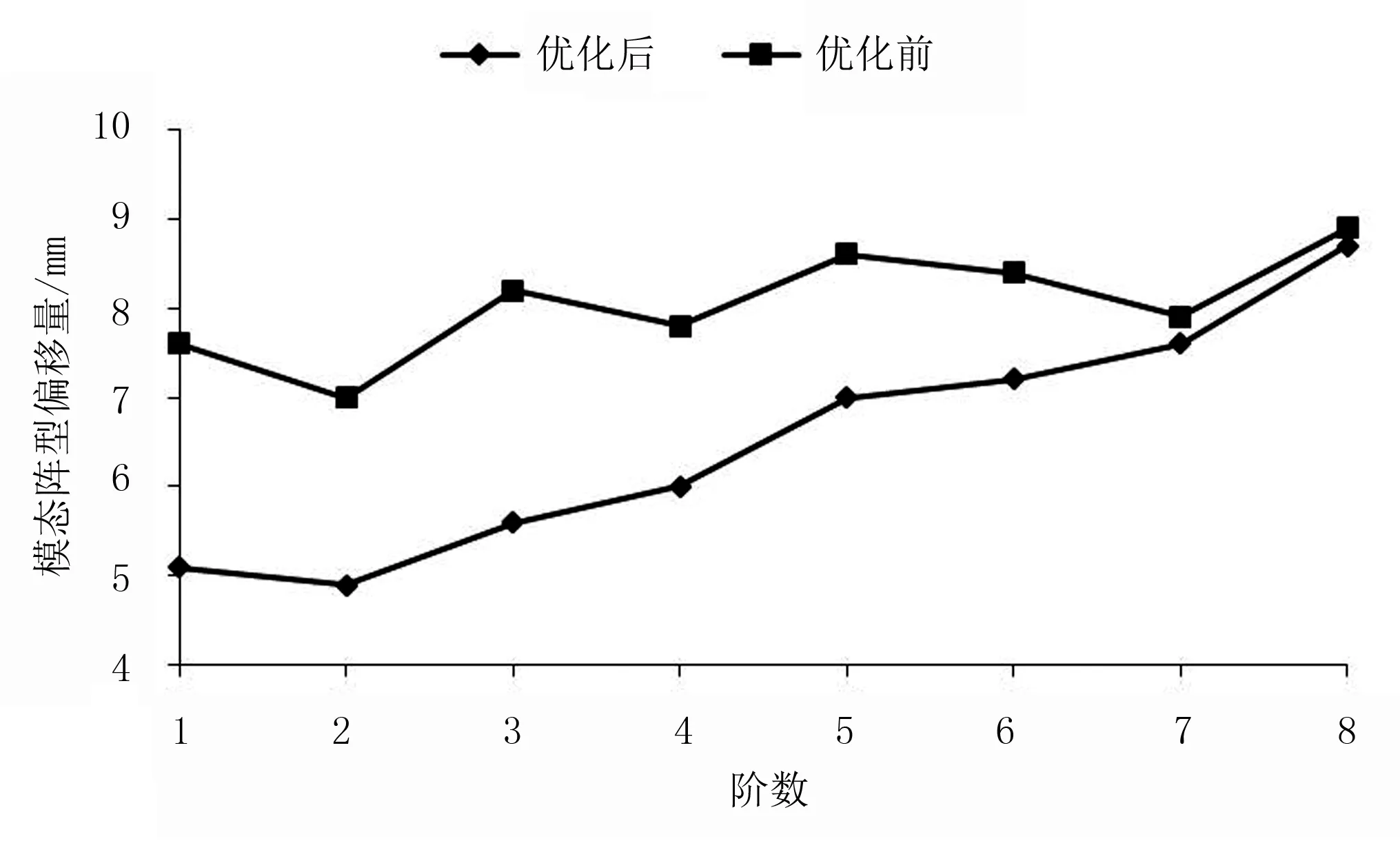
图8 优化前后模态阵型位移对比图

优化前后喷雾机喷杆的前8阶固有频率和阵型描述如表2及图9所示。

表2 优化前后各变量值对比

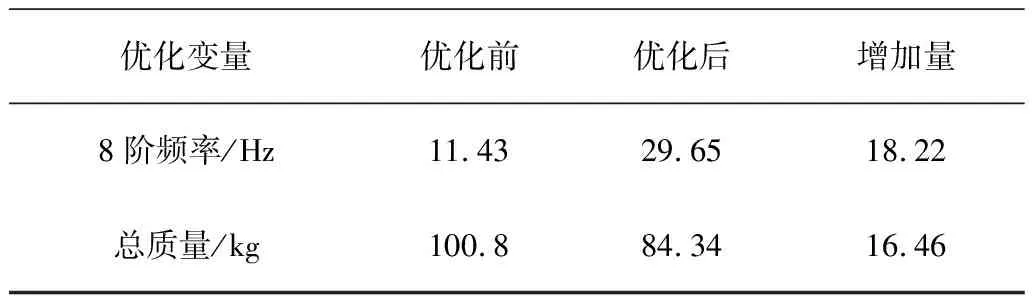
续表2

图9 优化前后前8阶固有频率对比图

优化结果表明：在喷杆的质量减少16.3%的情况下，喷杆的1阶固有频率增加9.56Hz，2阶固有频率增加11.87Hz，有效避开了喷杆的共振区间，减轻了喷杆整机的振动。同时，对比优化前后喷杆的分析结果可以看出：优化后喷杆的频率集中在10～50Hz，优化后喷杆的低阶固有频率远离了路面激励以及容易引起共振的频率区间，实现了固有频率的提升，从而优化了喷杆的动力学特性。此次拓扑优化的使得喷杆结构在田间作业时运行会更加平稳，极大地减小了发生共振的概率，在材料最佳分布的情况下，实现了喷杆最优的动力学性能。

4 结论

1)采用变密度法对喷杆进行拓扑优化，分析比较优化前后喷杆的动力学特性。结果表明：优化后的第1阶模态位移变形从7.6mm减小为5.1mm，第2阶模态位移变形量从7mm减小到4.9mm，极大地改善了喷杆整机的振动。

2)在喷杆整机质量减小16.3%的情况下，喷杆的1阶固有频率提高9.56Hz，可以有效避免激励源的共振区间，减轻喷杆的振动。