植保机可变量喷雾鲁棒控制
张凯丽,王向东,李树江,郑 薇
(沈阳工业大学 信息科学与工程学院,沈阳 110870)
0 引言
精细农业是现代农业发展的必然趋势,在施药方面人们一直研究变量喷雾技术,旨在通过提高农药的利用率来减少对环境的污染问题。目前,需要设计出功能更加良好的控制器,以满足精准农业对稳定性能、动态性能、控制精度及全工况调节性能的高精度要求,主要通过改进控制算法和优化电磁阀结构[1-5]的方法来提高控制性能。在控制算法上,很多学者依据具体的场合设计出相应的控制算法。WINDROW等[6-7]于1985年想出了比较完善的自适应逆控制理论,将该理论引入到控制问题的研究中,得出了一种控制参考模型,这种模型对每种类型的对象都能够实用;存在的不足是自适应逆控制一定要先通过迭代辨识系统的模型,才得以构建系统的自适应逆模型。刘志壮等[8]为变量喷雾系统设计了机电流量控制阀,并建立了流量控制阀的传递函数模型,设计了模糊控制算法,还对阀进行了模糊控制和PID 控制的 MatLab仿真。通过对上述两种算法的比较可知:由于模糊控制具有适应能力强和超调量小等优点,因此可以选择模糊控制算法对机电流量控制阀进行控制;但是,在现实变量喷雾的过程中,为了满足精准控制的目的,实际的响应时间一定要通过实际测量响应曲线的方法获得,而且变量喷雾控制的超前时间需要通过响应时间、植保机械行走的速度及农作物的位置来确定。陈树人等[9]依据实验所获得的数据,设计了自适应神经模糊控制器,并通过神经网络理论制定了5条模糊规则,当植保机速度和杂草面积发生变化时,自适应神经模糊控制器根据制定的模糊规则实时进行变量喷药。仿真结果表明:自适应神经模糊控制方法与传统模糊控制方法相比,具有自适应性强、控制效果良好、可减少药剂用量等优点,有助于保护环境,在今后的应用中具有一定的实用价值。但是,它目前仍处于实验室阶段,只有提高控制器的响应速度及控制精度,才能实现产业化。
本文根据系统的数学模型,设计了最优鲁棒输出跟踪控制器,使实际输出流量跟踪到目标值,并采用MatLab对其进行了仿真,得到了比较满意的控制效果。
1 系统数学模型
本研究的变量喷雾系统主要由药箱、给药泵、比例溢流阀和相互并联的多个喷雾单元组成,每个喷雾单元由比例减压阀、电磁阀、喷杆、喷头、压力传感器和流量传感器构成。变量喷雾系统原理简图如图1所示。
在工作过程中,CCD摄像机被安装在植保机的前面,以获取喷药目标的图像信息,这些信息通过图像采集卡送入计算机进行处理;同时,雷达传感器、 压力传感器和流量传感器同步将辅助信号通过I/O模块送入计算机进行处理;计算机将处理结果分别送至控制器,不仅可以控制各个喷雾单元进药的多少,还可以控制电磁阀的开关,从而实现各喷雾单元喷药和停喷的状态;计算机还把喷药量的信号由I/O模块传送到每个喷雾单元的比例减压阀上,通过改变阀的控制电流,控制阀的输出压力,从而调节各喷雾单元的工作压力,通过喷头实现变量喷雾。

1.电源 2.给药泵 3.比例溢流阀 4.过滤器 5、8、14.电磁阀 6.药箱 7.CCD摄像机 9.雷达传感器 10.嵌入式计算机 11.比例减压阀 12.流量传感器 13.压力传感器 15.喷头
本文选用的控制阀为比例减压阀,由电磁铁、阀芯和液压流体组成。电磁阀所受的电磁力和通过线圈的电流呈近似线性关系。当电磁阀线圈通电,电流不断变大时,衔铁所受到的电磁力也会随之逐渐增加,当电磁力大于电磁阀右端所受弹簧预紧力,电磁铁推动阀芯移动,此时球阀打开,药液流进药液腔内,输出口由压力输出转化为流量输出。由于流体的流量和压力之间存在关系,所以可以通过调节喷药口的开口大小,控制药液口的压力,进一步可以控制输出口的流量。喷药口处的药液压力会随着电磁阀进药口药液压力的增大而增大,作用在阀芯喷药口处的端面,当阀芯受到的作用力大于电磁力的作用时,阀芯向左移动,导致喷药口的开度随之增大,达到溢流的目的。通过改变电磁阀调节弹簧的长度,调节溢流压力值的大小。综上所述,根据电磁阀的工作原理,开始时由于阀芯所受弹簧力的作用,确保在没有给电磁阀通电的情况下,电磁阀一直处于关闭状态;当电磁阀通电以后,很小的电磁力就可以使阀芯产生位移,加快了电磁阀的响应速度,便能使电磁阀快速打开。因此,当液压流体部分结构不变时,电磁力的设定不仅要很小得以达到电磁阀溢流的标准,而且要满足电磁铁推力相对于阀芯位移成近似线性关系。
1.1 磁路方程
由于电磁阀所受的电磁力与驱动电流呈近似线性相关,因此有必要在电磁阀的驱动回路中引入电流反馈,提高驱动电液的一致性,增强驱动电路的可靠性。线圈通电后产生的电磁力Fm[10]为
若令
则有
Fm=kFi2
(1)
其中,δ为线圈与衔铁之间的气隙;N为线圈匝数;Sa为有效作用面积;μ0为真空磁导率;i为线圈中的电流。
1.2 运动方程
工作过程中,对电磁阀进行受力分析,主要受到以下几方面力的作用:①电磁阀阀芯加速运动而产生的质量惯性力;②推杆移动后所产生的粘性阻尼力;③线圈通电后产生的电磁力;④阀芯所受的弹簧力。建立模型时忽略流体动量变化产生的稳态液动力和瞬态液动力以及液体静压力,因此得到阀芯的运动平衡方程[11]为
(2)
其中,m为阀芯的等效质量;c为阀芯的等效阻尼;x为阀芯的位移;x0为预先弹簧压缩量;k为弹簧刚度;kF为比例系数。
1.3 流量方程
电磁阀的流量方程[12]为
令
则有
Qf=a(P)x
(3)
其中,Qf为通过阀口的流量;Cf为流量系数;Sa为有效作用面积;x为阀芯的位移;P为出口压力;ρ为药液密度。
根据方程(2)、(3)建立状态空间为
由式(2)、式(3)有
y=Qf
则有

(4)

在模型(4)的计算中,状态方程可表示为
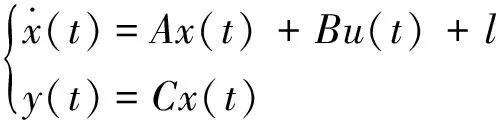
(5)
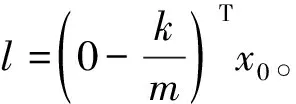
本文所涉及到的一些有关电磁阀的数据参数来自于文献[12],如表1所示。
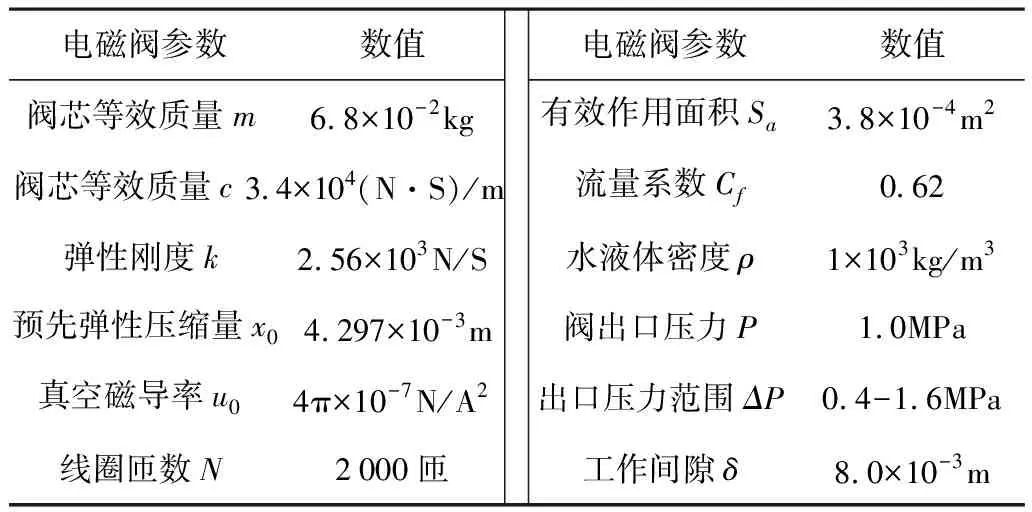
表1 电磁阀的数据参数
将上述工作点带入状态方程,出口压力取中间值1.0MPa,得到方程中各矩阵A、B、C与常数矩阵l为
由于需要对电磁阀出口的流量进行合理有效地控制,因此需要设计一个控制器。一般情况下,需要把方程转换成标准的线性状态方程,因此要对常值矩阵l进行变换,设定输入u=u1+u2。在此公式中,预设定的控制器为u1,通过计算取u2=0.737 2,即满足Bu2+l=0。那么,便可以通过控制输入u2消除l,于是可以得到标准的二阶线性状态方程,即

(6)
本文中,由于出口压力的不确定性,使得模型参数存在一定的误差,使所得的模型具有不确定性。将参数的不确定性用不确定矩阵ΔA表示,不确定矩阵ΔA主要依赖于压力P的变化,则不确定线性系统的方程变为
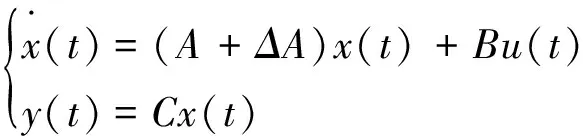
(7)
并且这里的ΔA能满足下述特征,即
ΔA=EθF
(8)

2 鲁棒输出跟踪控制器设计
跟踪问题是控制中的主要问题之一,要想进行很好的跟踪,则需要使系统的输出值尽可能地追踪到外部的参考值。在1970年初,就已经解决了线性确定系统的跟踪问题;但由于考虑到现实情况,被控对象本身的特性会随使用时间或生产过程发生变化[13],所以得到的模型一般都会存在着参数不确定性的现象。在本文中由于出口压力的不确定性,使得模型参数存在一定的误差,使所得的模型具有不确定性。所以,本文引入一种鲁棒控制方法来对带有不确定性的变量喷药系统的喷药量进行鲁棒控制。
考虑不确定线性系统的一般方程,则
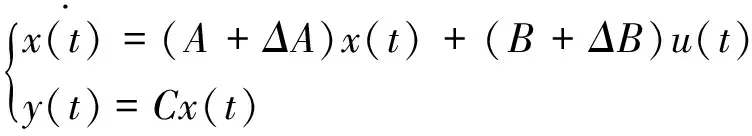
(9)
其中,x(t)∈Rn作为状态向量,u(t)∈Rm作为控制向量,y(t)∈Rp系统的输出向量;A、B、C依据模型而具有的合适维数的标称矩阵,ΔA和ΔB与矩阵A和矩阵B维数一致的不确定性矩阵。
就鲁棒控制器的设计而言,首先需要建立一个増广系统。本文所设计的控制目标是使系统的实际输出值流量值渐近跟踪到所设定的目标流量值,在t→时,能够使实际输出流量值与目标流量值之间的差值收敛到0,用公式可以表示为
(10)
为了能够让系统的输出误差向量e(t)=y(t)-yr敛到0,需要对误差向量进行积分处理,便可消除向量的误差,从而使误差为0,用公式可以表示为
(11)
将式(11)与本文控制系统中的状态方程联立,得到增广系统为
(12)
将上述方程重新整理为一个增广的状态方程的形式,即
(13)
其中,
并且这里ΔAz满足下述特性,即
ΔAz=EzθFz
(14)

为了能够达到控制器使系统稳定这一标准,本文所设计的性能指标只要满足线性系统是可控的即可,而最优控制不仅可以使输出流量值跟踪到目标设定的流量值,还能使性能指标达到最小值。系统的性能指标描述为
(15)
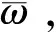
根据传统的最优控制方法,控制量为
u(t)=-ρ-1BzTPz(t)=-kz(t)
(16)
在这里P为对称正定解,并且是如下的 Riccati方程的稳定解,即
(Az+εIz)TP+P(Az+εIz)-ρ-1PBzBzTP+ζIz=0
(17)
其中,Iz为单位矩阵。
由于系统具有不确定性,因此推导出最佳的控制输入为
u*(t)=-Kz(t)=-(1+α)kz(t)
(18)
在这里α是调节因子,满足
(19)
3 仿真结果及分析
通过设计的鲁棒跟踪控制器的方法进行鲁棒控制器的设计,并选择指定的收敛率ε值为2,在性能指标中的加权参数ζ为2,ρ=2,设0≤r1≤1,0≤r2≤1并依据文中的公式,通过计算得出α=1,则对称矩阵P和最优反馈增益K为
P=
K=
[3.394973×1067.197748×10-26.790007×106]
本文对电磁阀输出的流量进行仿真,在MatLab的仿真环境下编写程序,用求解微分方程解的函数ODE45编写函数,编写基于鲁棒输出渐进跟踪方法设计鲁棒控制器的程序,并对其进行仿真,验证所设计的鲁棒控制方法的有效性。
1)取初始点为Z0=[8 2 1]的情况下进行仿真。当给定的电磁阀出口目标流量为20L、r1=0、r2=0时,在MatLab仿真工具中编写程序。仿真得到输出流量曲线和输出误差曲线如图2所示。

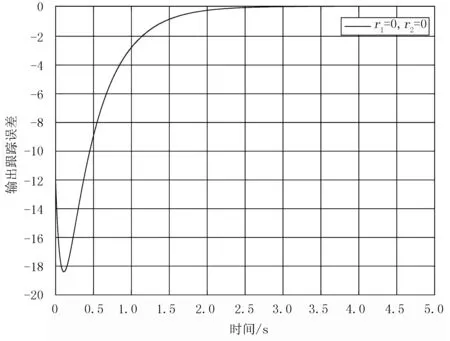
图2 输出流量/误差曲线图(r1=0,r2=0)
由图2可看出:在预设目标流量为20L时,基于最优算法的鲁棒输出跟踪控制流量,在初始输出流量为8L时,电磁阀输出流量的图像开始迅速下降,在0.1s附近时图像相对快速增长,并逐渐达到预设定的目标输出流量20L;当不确定参数r1、r2同取0时,即不存在不确定量的情况下,系统能够保持稳定。从两幅曲线图中能分析出,在初始点处进行仿真,其输出流量出现急剧下降并在控制器的控制作用下,上升并平缓的将实际输出流量跟踪到目标流量20L,且跟踪曲线逐渐接近于0。
当给定的电磁阀出口目标值为20L、r1=1/2、r2=1/2,在MatLab仿真工具中编写程序,得到的流量曲线和输出误差曲线如图3所示。
由图3可看出:在预设目标流量为20L时,变量喷药系统的输出流量在8L时,电磁阀输出流量的图像开始迅速下降,在0.1s附近时,图像相对迅速增长并逐渐达到预设定的目标输出流量值20L;当不确定参数r1、r2同时取1/2时,在系统存在不确定量的情况下依然能保持其稳定性,并且在输出误差为2.5s时收敛到0,能够满足实际输出流量值渐进跟踪到预设定的目标流量值,从而证明本文所设计最优算法的鲁棒输出跟踪控制算法对变量喷雾系统输出流量控制的可行性,具有良好的控制效果。
2)在初始点Z0=[13 2 1]进行仿真。当给定的电磁阀出口目标流量值为20L、r1=1/2、r2=1/2,在MatLab仿真工具中编写程序,得到的流量曲线和输出误差曲线如图4所示。
由图4可看出:在预设目标流量值为20L时,实际的出口流量在初始值为13L时,图像开始急速下降,在0.1s时迅速增长,并在2.5s时达到预设定的目标输出流量值20L;当不确定参数r1、r2同时取1/2时,在系统存在不确定量的情况下依然能保持其稳定性,跟踪误差也很快收敛到0,从而证明了本文所设计的鲁棒控制器能使实际输出流量值快速跟踪到目标设定的流量值,不仅跟踪性能良好,而且反应快。
仿真结果表明:所设计的鲁棒跟踪控制器能很好的跟踪输出流量,能使实际流量快速跟踪目标设定值,即使参数目标不确定,即r1、r2存在时,所设计的鲁棒控制器也能保证系统的稳定性,说明对于流量的输出控制具有可行性,且鲁棒性能良好。


图3 输出流量/误差曲线图(r1=1/2,r2=1/2)


图4 输出流量/误差曲线图(r1=1/2,r2=1/2)
4 结论
以变量喷雾系统中的比例减压阀作为被控对象,建立了喷药系统的数学模型,为对电磁阀输出的流量进行控制,设计了最优鲁棒输出跟踪控制器。首先,依据系统的运动方程和流量方程建立系统的数学模型,由于数学模型中压力存在不确定性,因此将不确定性代入空间状态方程中,最后求得系统模型为两阶的不确定性线性系统状态空间模型。其次,依据所构建的变量喷雾系统的数学模型,设计最优的鲁棒输出跟踪的控制方法,并设计出对电磁阀输出流量的实际值进行跟踪控制的控制器,并在MatLab仿真软件中对设计的鲁棒跟踪控制器进行仿真验证,作出电磁阀输出流量及输出跟踪误差的曲线图。仿真结果表明:所设计的鲁棒跟踪控制器能使输出的流量值跟踪到目标值,并有很好的鲁棒性,可对变量喷雾系统输出的流量进行有效控制,使系统能稳定安全的运行。

