探究高中阶段三角函数学习的心得体会

李 玲

(江苏省东海县石榴高级中学 222314)

一、高中三角函数的学习意义

一方面，强化学生的逻辑思维能力.与传统数学知识不同，三角函数可以结合现实图形进行问题探索，因此数形结合是当前课堂教学最常用的一种方法.由于高中阶段的三角函数中涉及很多基础知识，不仅繁琐而且零碎，所以在实践做题中要一步步推算，这也是解决问题的关键所在.由于解题思路有很多种方式，所以学生在探索问题时可以充分锻炼他们的逻辑思维能力；另一方面，可以在其他学科整合运用.以物理曲线绘制为例，其中就涉及部分三角函数知识.通过学好高中三角函数，既可以提高学生学习水平，又可以在全面认识三角函数的基础上，解决实践问题.因此，在三角函数教学持续优化中，教师要优化自身的教学模式，注重引导学生更加完善地掌握与应用三角函数相关知识，以此实现预期设定的教学目标.

二、当前高中三角函数学习难点分析

在初期接触三角函数知识时，学生会觉得学习难度大，且随着学习方式的转变，难以尽快适应课堂环境，更不会积极参与教师设计的教学活动，这样不仅无法提升课堂教学效率，而且会限制学生学习的自主性与积极性.从课堂教学案例分析可知，常见难点分为：其一，没有形成良好的学习习惯.由于高中三角函数包含的基础理论知识非常多，且要系统研究相关内容，如图象、单调性、周期性等，如果学生没有形成良好的学习习惯，将无法充分掌握所学知识，而且会影响他们的认知水平与理解能力；其二，解题有难度.在学习高中三角函数知识时，由于学生没有产生正确认知，且缺少系统的知识体系，所以在解题时很容易出错，长此以往很容易让学生产生抵触心理，并降低实践学习效果；其三，没有综合研究问题意识.高中生在解决问题时，会遇到涉及多个知识点的难题，不仅解决起来麻烦，而且会影响学生学习效果.但若运用综合分析思维对问题进行研究，可以有效解决这些问题.但了解当前高中生可知，他们并没有认识到这项技能的重要性，且没有在实践训练中进行培养与优化，致使最终面对的三角函数问题越来越难解决.

三、高中阶段三角函数学习心得分析

1.构建良好学习习惯

一方面，要具备自主思考意识.通过在课上课下培养学生自主思考意识，并正确观察与分析与三角函数有关的知识，不仅能活跃课堂教学氛围，而且可以提升学生水平.例如，在学习“象限角”时，因为角的顶点就是坐标原点，且始边与x轴的正半轴重合，因此角的终边落在哪个象限，就叫做第几象限的角.需要注意的是，若角的终边落在坐标轴上，那么这个角不属于任何象限.在这一过程中，教师可以让学生在演算纸上画出对应的坐标轴，并根据教师的提示绘画正确的“象限角”，如30°、-330°等都属于第一象限角；1180°属于第三象限角等.同时，还要让学生观察判断30°和-330°角的终边是否相同.此时，学生不仅会充分调动自身思维解决数学问题，而且会积极参与课堂教学知识，并形成自主思考意识；另一方面，构建学习精细化知识分析的习惯.在高中数学教学中，通过熟练掌握所学知识，正确理解与三角函数有关的性质与概念，并学会构建三角函数模型解决问题，严格按照三角函数知识规律分析问题，有助于提升学生学习水平.

2.熟练掌握解题技巧

在学习三角函数知识时，教师要指导学生了解各类知识之间的关联性，并注重强化数学思想与思维意识的培养力度.对实践教学工作而言，教师可以在教学中运用数形结合的思想，先从周期性入手研究相关数学模型，这样不仅能从基础上理解三角函数，而且可以优化学生数学学习水平.同时，在解题时，还要让学生累积解题经验，注重熟练运用解题技巧，更好落实实践学习任务.例如，教师在引导学生学习“三角函数的图象与性质”时，一方面要让班级学生熟练掌握图象和性质，并且可以运用数形结合的思想，将两者整合到一起；另一方面，要组织学生自主思考与发掘，并在实践训练中优化他们的思维形成过程.同时，还要结合不同的观点进行问题分析，而后对数形结合有更深认识，最终培养学生优质的数学品质.因此，在完成基础内容教学后，教师要为学生设计如下例题进行图象与性质的深层探索：

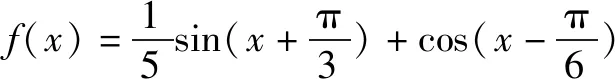
在上述问题的探讨中，学生可以熟练运用所学基础知识解决问题，并绘画对应图象进行自主探讨.在这一过程中，他们不仅能累积大量解题经验，而且可以优化自身数学学习水平，并形成自主学习意识，这对未来数学教学而言至关重要.

3.构建综合学习思维

要想更好实现预期教学目标，提升课堂教学效率，优化学生学习能力，必须要为学生设计具有针对性的习题，促使他们在总结经验的同时，形成正确的思维模式与学习态度.这样不仅能有效处理三角函数问题，而且可以为后续教学奠定基础.

综上所述，高中三角函数知识并没有想象的那么难，相反只要学生熟练掌握基础知识，并积极思考和探讨教师设计的数学问题，就可以在训练中掌握更多计算技巧，并充分发挥他们的学习思维.同时，在完成课堂教学任务后，教师还要针对班级学生学习水平设计复习习题，以此确保学生可以在寻找解题思路中，降低高中三角函数知识学习难度，并实现预期课堂教学目标.