扇形凹穴型微通道流动与传热的场协同与熵产分析

张 颖，冯振飞 ，2

（1.广西大学机械工程学院，南宁 530004；2.广西大学广西石化资源加工及过程强化技术重点实验室，南宁 530004）

0 引言

换热器广泛应用于化工、航空航天和制冷等各个工业领域。随着科技的不断进步，各行业对换热器的换热效果提出了更高的要求，包括要求换热器向微型化方向发展。常规尺度通道的换热器向微型化发展就形成了微细通道换热器。通道直径越小，传热系数就越高[1]。微细通道换热器较高的传热系数促使其成为研究者们关注的热点。为了使微通道换热器满足更大的热负荷换热需求，研究者们不断探索其强化传热方法。被动式强化传热不需要额外提供能源，成为研究者们主要的研究方向。

在微细通道内设置凹穴结构也属于被动式强化传热方法。Pan等[2]实验研究了扇形凹穴型微通道换热器的传热特性。Alfellag等[3]在直细微通道内加入梯形凹穴，并在凹穴内设置椭圆形针肋，研究尺寸改变的最优传热效果，结果表明，在研究范围内尺寸参数最优时的最大综合传热因子约1.37。Ma等[4]研究了在侧壁设置周期性喷射节流凹穴结构的微通道热沉的换热效果，研究发现，节流型微通道热沉的综合性能因子约为喷射型微通道热沉的2.5倍。Ghani等[5]研究了正弦型凹穴内置矩形肋的流动传热特性。Liu等[6]对设置扇形凹穴的环形微通道进行数值模拟，研究尺寸参数对微通道传热和流动特性的影响。冯振飞等[7]用对比方式研究了扇形凹穴结构对直细微通道和螺旋形微通道的流动传热特性影响，结果表明，凹穴不能提高螺旋形微通道的综合性能，但提高了直细微通道的综合性能，最大强化传热因子达1.27。贾玉婷等[8]研究了等直径段有不同夹角的水滴形凹穴微通道的流动传热特性。

从上述研究发现，研究者们往往基于热力学第一定律对凹穴型微通道的流动与传热特性进行研究，而基于热力学第二定律的研究较少。此外，凹穴结构对微通道流动和传热影响的内在本质尚未明晰。本工作是在前期扇形凹穴型微通道研究[7]的基础上，对扇形凹穴型微通道流动与传热进行场协同和熵产分析。具体是基于场协同理论，分析扇形凹穴结构参数对微通道内速度矢量与压力梯度及速度矢量与温度梯度的协同程度影响。并用热力学第二定律，分析流体流动和传热过程中的不可逆损失，最后用熵产增大数来描述扇形凹穴结构对各参数微通道能量损失的影响。研究成果可进一步揭示凹穴结构对微通道流动和传热影响的内在本质。

1 模型描述

1.1 物理模型

扇形凹穴型微通道（简称凹穴微通道，Microchannel with Cavities，MCC）是在传统的光滑微通道（Micro-channel，MC）基础上，加入扇形凹穴结构而形成的，其结构尺寸如图1所示。微通道的宽Wch=0.5 mm，高Hch=1 mm，微通道计算域宽W=1.5 mm，高H=1.5 mm，半肋宽a=0.5 mm，微通道长L=40 mm。基于上述尺寸得到微通道当量直径Dh=2WchHch/（Wch+Hch）=0.667 mm。根据不同的扇形凹穴尺寸R（整个扇形的圆半径）和相邻扇形凹穴间距S，可得到5种凹穴微通道结构，分别命名为MCC-0.5-1（R=0.5 mm，S=1 mm）、MCC-0.5-1.5、MCC-0.5-2、MCC-0.4-1.5、MCC-0.6-1.5，对应有31、21、16、21和21对凹穴，进出口与凹穴的距离b=5 mm。为了便于对比，建立了MC模型，其尺寸与上述一致。

图1 凹穴微通道结构示意图Fig.1 Schematic diagramof micro-channelwithcavities

1.2 数值模型

计算域模型如图2所示。固体域的材料为铜，其导热率为401.0 W/（m·K）；流体域的材料为去离子水，其密度997.0 kg/m3、黏度为8.899×10-4Pa·s、比热为4 181.7 J/（kg·K）和导热率为0.606 9 W/（m·K）。为了防止发生出口回流现象，在微通道出口处设置了长为40 mm的过渡段。

为了简化计算，假设本研究的流体的流动状态为连续且稳定的层流状态；在热传递中流体和固体的物性稳定不变；忽略体积力、热辐射影响和热量损失。由此，流体域的连续性方程、动量方程和能量方程可以简化为：

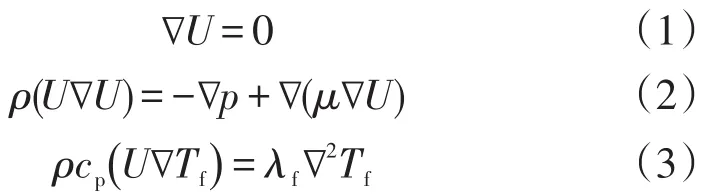
图2 计算域模型Fig.2 Camputational domain moldel

由于固体域是没有速度的，其能量方程为：

式（1）～（4）中：下标s和f分别代表固体和流体；U为速度矢量，m/s；ρ为该流体在某温度下的密度，kg/m3；μ为该流体在某温度下的粘度，Pa·s；cp为该流体在某温度下的比热，J/（kg·K）；p为压力，Pa；T为温度，K；λ为导热率，W/（m·K）。

在数值模拟计算之前需进行边界条件设置。微通道进口采用进口速度边界条件，进口温度Tin=293 K，进口速度uin为0.4～2 m/s，根据式（5），可得到雷诺数Re为298.76～1 493.80；微通道出口设为压力出口边界条件，出口压力pout=0 Pa（相对环境压力）；微通道的底面采用恒热流边界条件，热流密度q=400 kW/m2；固体和流体域接触部分设置为固液交界面边界条件，没有速度滑移和渗透；由于热沉内的多微通道具有周期性，因此研究的单个微通道计算域的两侧面采用周期性边界条件；模型剩余的壁面均为绝热边界条件。

上述控制方程组用CFD软件进行数值模拟求解，收敛残差为10-5。在数值求解之前需对6组模型的各个计算域进行网格划分。鉴于模型的复杂程度，采用四面体和六面体的混合网格对其进行划分，所有模型的网格数维持在130万左右。根据进口速度的变化（0.4、0.6、0.8、1.0、1.2、1.4、1.6、1.8、2.0 m/s），每个模型数值模拟9个工况，6组模型，共54个算例。

2 数据处理

平均摩擦阻力系数f的计算公式为：

式中：Δp为微通道段进出口的压降，Pa。

Shah等[9]发现，矩形直通道在正在发展的层流状态下，其平均摩擦阻力系数的理论计算式为：

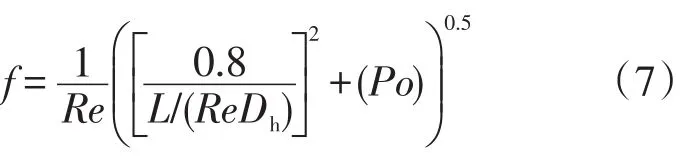
其中：

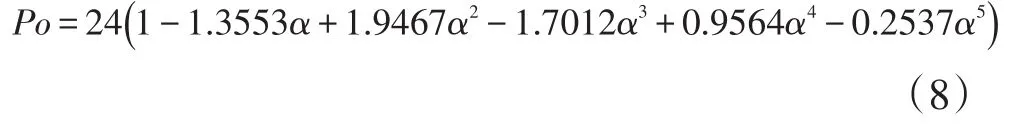
式中：Po为泊肃叶数；α为微通道的宽高比。平均传热系数h的计算式为：

式中：Aw和Aif分别为加热面和流固传热面的面积，m2；Tw和Tout分别为加热面和通道出口的平均温度，K。

平均努赛尔数Nu的计算式为：

根据能量守恒，微通道进出口温差的理论计算公式为：

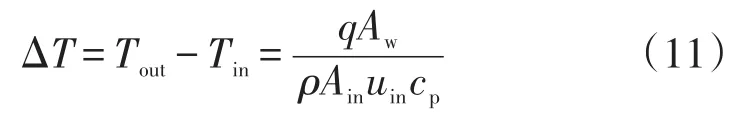
式中：Ain为微通道进口截面面积，m2。

根据Gao等[10]提出的场协同理论，可得到流体速度矢量与温度梯度之间的协同关系表达式为：

式中：β为速度矢量和温度梯度之间的协同角。协同角β越小，场协同效果越好，越有利于传热。

同理可得到流体速度矢量与压力梯度之间的协同关系表达式为[11]：

式中：α为速度矢量与压力梯度之间的协同角。协同角α越小，流体流动所消耗的泵功就越少。

式（12）和式（13）中的协同角为0～180°，为了便于分析，取绝对值来说明协同角，其在0～90°之间。即α和β的计算式分别为：

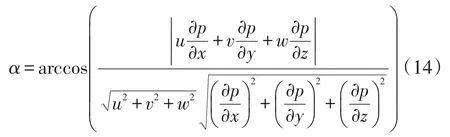
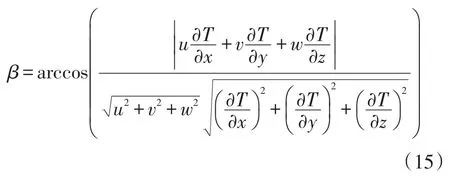
式中：u、v和w分别为x、y和z的速度，m/s。

微通道热沉内部流体之间的对流传热包含流动过程和传热过程，按照热力学第二定律，流体流动过程中压降造成摩擦损失耗能，对流传热过程中因温差存在造成传热能量损失。采用熵产原理分析微通道流动和传热过程的不可逆损失。流动过程中产生的流动熵产SF定义为[12]：

式中：m为质量流量，kg/s。

传热过程中的传热熵产SH定义为[12]：

总熵产Sg为[12]：

为了更清晰的体现MCC相对MC的节能程度，引入熵产增大数评价各个微通道热沉的综合性能。熵产增大数定义为[12]：

式中：Ns，a代表熵产增大数，无量纲；Sg，0为光滑微通道的总熵产。Ns，a值小于1表明总熵产相对光滑微通道而言有所减少，Ns，a值越小，不可逆损失越小。

3 数值模拟有效性验证

为了验证所采用的数值模拟方法的有效性，选择光滑微通道的数值模拟结果和理论计算结果进行对比。图3为光滑微通道摩阻系数和进出口温差的理论计算值与模拟值的对比结果。因为微通道内的流体状态是正在发展的层流，所以式（6）和式（7）中的L包含过渡段长度，即L=80 mm。

政府应该放宽出租车行业的准入机制，不仅要鼓励更多的企业参与到出租车行业的运营当中，将出租车数量的控制权交给市场进行管制，还可以通过更多的法律制度规范来约束整个出租车行业，更多地实施监管的责任，保证乘客的安全，提高人们对出租车的选择率。

由图3可知，在所研究的雷诺数范围内，光滑微通道摩阻系数的理论值和模拟值比较吻合，最大误差为15.79%；光滑微通道的进出口温差的理论值和模拟值非常接近，最大相对误差为1.55%。由此可见，所采用的数值模拟方法是可靠有效的，该方法也可以用于计算分析凹穴微通道的流动和传热特性。

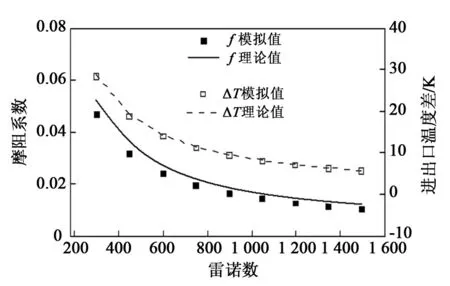
图3 光滑细通道摩阻系数和进出口温差的模拟值与理论值的对比曲线Fig.3 Comparisons between simulation and theoretical data of friction factor and temperature difference between inlet and outlet in smooth micro-channels

4 结果与讨论

4.1 流动与传热特性分析

图4为用式（6）计算得到的雷诺数范围内各结构摩阻系数的变化趋势。由图4可见，随着雷诺数增加，摩阻系数逐渐变小；在同一雷诺数下，各个微通道的摩阻系数各不相同，扇形凹穴型微通道的摩阻系数均高于光滑微通道。经计算，MCC要比MC摩阻系数平均高约53.6%；相比MC，MCC-0.5-1.5阻力变化最大，摩阻系数平均高约72.6%；MCC-0.6-1.5摩阻系数变化最小，平均高出约36.9%。

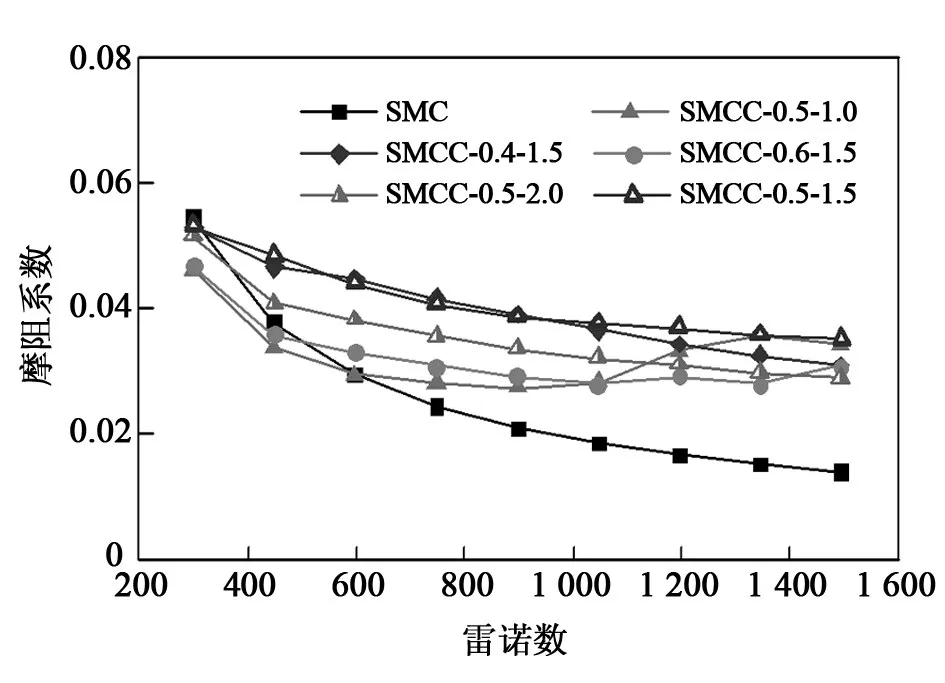
图4 摩阻系数f随雷诺数Re的变化曲线Fig.4 Variation of friction factor f with Reynolds number Re

图5 是由式（9）算得的传热系数随雷诺数的变化趋势。由图5知，传热系数随着雷诺数变大而变大；在多数工况下，相对于MC，MCC的传热系数均有所增加，计算得平均高约28.95%，说明扇形凹穴结构提高了微通道的传热效果。其中MCC-0.5-1.5传热系数最高，相比MC平均高约40.02%。

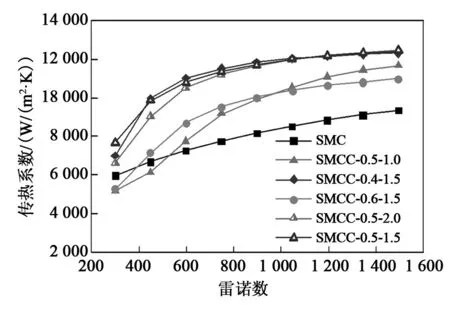
图5 传热系数h随着雷诺数Re的变化曲线Fig.5 Variation of heat transfer factor h with Reynolds number Re

4.2 场协同分析

图6 给出了6种微通道的速度矢量和压力梯度间的协同角云图。由图6（a）发现在MC整体区域内协同角α较小，说明速度场和压力场协同程度很高，这由于流体在直通道内沿程压降是沿着流动方向下降的，压力梯度和速度矢量的方向就比较一致。所以一定程度上协同角α的大小，能够体现能量的利用程度，即流体容易从压力高的位置流向压力低的位置。观察图6中5种MCC的云图，发现协同角α较MC均有所增加。显然在局部区域内尤其是扇形凹穴区域内，由于流动扰动作用增强，压降突然增大，这与光滑微通道内压降是沿着流动方向逐渐减小的现象相反。因此，MCC通道局部位置的压降梯度方向发生改变，导致协同角α变大。故而，相对MC，扇形凹穴结构增加了微通道的阻力损失，降低了能量利用程度。

图6 6种微通道的速度矢量和压力梯度间的协同角α云图（进口速度u in=1 m/s）Fig.6 Contours of synergistic angle α between velocity vectors and pressure gradients for six micro-channels（inlet velocity u in=1 m/s）

图7 是6种微通道的速度矢量和温度梯度的协同角β云图。对比图7各图可见，在整个MC内，速度矢量方向和温度梯度的方向是相反的，这点在另外5种MCC的直通道部分也很明显。而在扇形凹穴区域，发生层流边界层中断、流体扰动增强等作用，甚至产生不断循环的二次流，致使凹穴区域的速度矢量方向随着流动扰动和二次流作用发生改变，进而减少了局部区域内速度矢量和温度梯度协同角β，甚至会出现β极小的局部区域。所以，扇形凹穴结构的加入改善了速度场和温度场的协同程度，减小了协同角β，强化了传热效果。

但是，云图只能体现局部协同角β的变化情况，不能定量的描述其大小，所以引入场协同数来计算不同进口速度下的微通道速度场和温度场的协同程度，场协同数定义为：

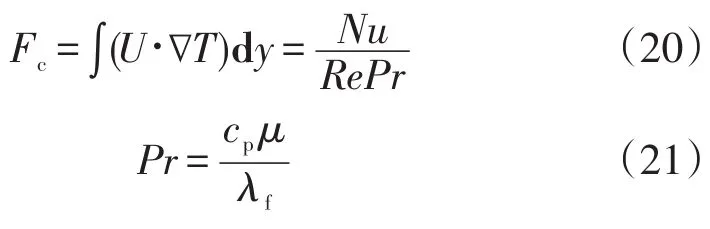
式中：Pr为普朗特数，无量纲。Fc为场协同数，是一个小于1的无量纲数，其值越大表示速度和温度场协同程度越高，越利于传热。

图8为场协同数随雷诺数的变化关系。由图8可知，随着雷诺数Re增加，场协同数Fc逐渐变小，这是因为微通道内流体流速过高时会削弱扇形凹穴结构的扰动作用，二次流现象减少，使场协同程度下降。在同一雷诺数Re下的大多数工况时，MCC的场协同数要高于MC。显然，扇形凹穴结构的加入改善了速度场和温度场的协同程度。经过计算，在所研究范围内，MCC-0.5-1.5的场协同数最大，平均约为0.002 94。

图7 6种微通道的速度矢量和温度梯度的协同角云图（进口速度u in=1 m/s）Fig.7 Contours of synergistic angles β between velocity vectors and temperature gradients for six micro-channels（inlet velocity u in=1 m/s）

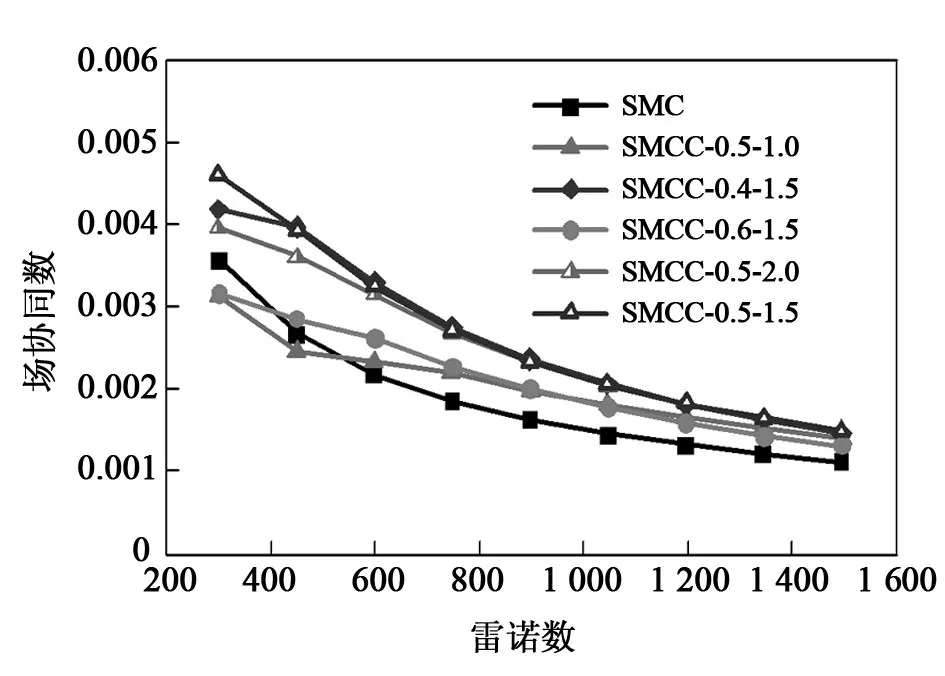
图8 场协同数F c随雷诺数Re的变化曲线Fig.8 Variation of field synergy number F c with Reynolds number Re

4.3 熵产分析

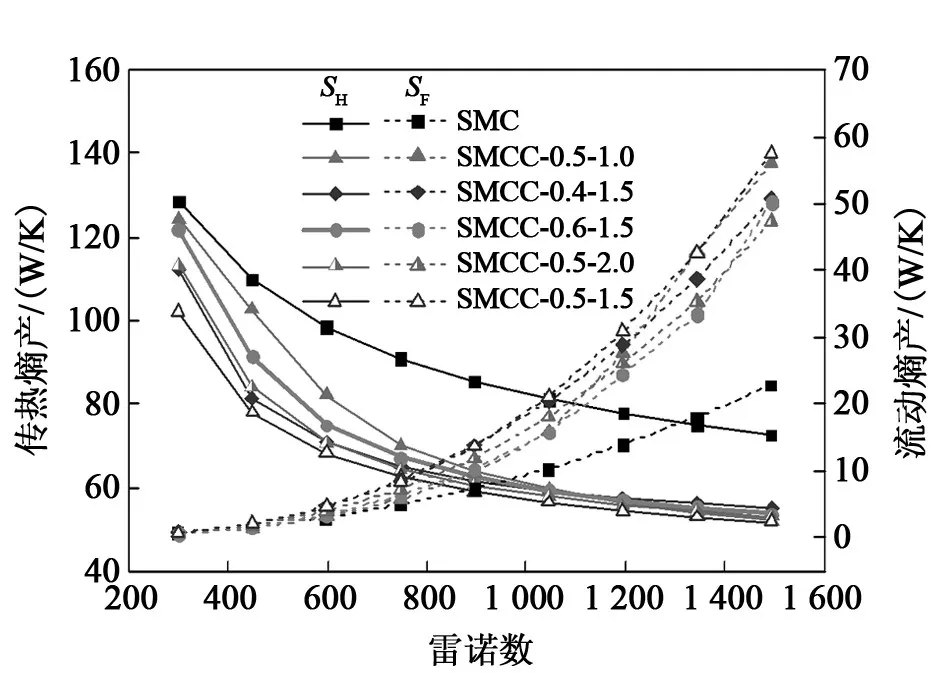
图9 6组微通道的流动熵产S F和传热熵产S H随雷诺数Re的变化曲线Fig.9 Variation of flow entropy generation S F and Heat entropy generation S H with Reynolds number Re in six microchannels

图10 为总熵产和熵产增大数随雷诺数的变化趋势。由图可知，随着雷诺数增大，总熵产逐渐减小，因传热熵产几乎可以代表总熵产，所以趋势与传热熵产基本一致；相对MC，MCC的总熵产均有所减小，表现为熵产增大数均小于1，说明，扇形凹穴结构虽带来阻力损失，但也带来更好的传热效果，总体上能够减少微通道的不可逆能量损失。根据熵产最小原则，计算可知MCC-0.5-1.5的熵产增大数最小，平均约为0.74，在Re=747附近工况下的最小熵产增大数约为0.69。

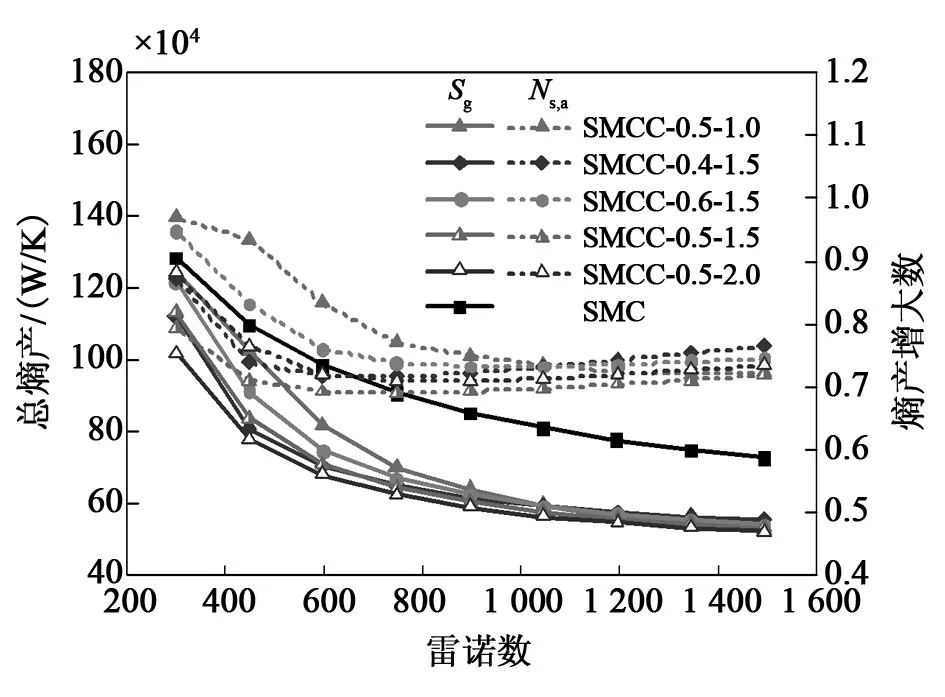
图10 总熵产S g和熵产增大数N s，a随雷诺数Re的变化曲线Fig.10 Variation of total entropy generation S g and augmentation entropy generation number N s，a with Reynolds number Re

5 结论

（1）对于光滑微通道而言，扇形凹穴结构增大了流阻，MCC的摩阻系数平均增加53.6%；扇形凹穴结构也提升了传热效果，MCC的传热系数平均提高了28.9%。

（2）扇形凹穴结构改变了MCC内局部位置压降梯度的方向，致使速度场和压力场协同配合程度下降，协同角α变大，扇形凹穴结构增加了微通道的阻力损失。

（3）流体在凹穴位置产生扰动和二次流作用，改变了局部区域速度场方向，速度场和温度场的协同角β有所减小，凹穴结构给微通道带来更好的传热效果。经过场协同数Fc的计算，MCC-0.5-1.5场协同数最大，平均为0.002 94。

（4）熵产分析表明，扇形凹穴结构给微通道带来的阻力损失远小于给微通道带来的传热效果，流动熵产的增大量远小于传热熵产的减小量，MCC的熵产增大数均小于1。其中，MCC-0.5-1.5的熵产增大数最小，平均为0.74。