星载铷钟频率漂移修正方法研究

王剑祥，张金海，陈溶波，涂建辉，杨 炜，崔敬忠

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

0 引言

铷钟具有体积小、质量轻、功耗低、可靠性高以及寿命长的优点，在导航卫星中得到广泛应用[1]，但是铷钟作为二级频标，主要存在几个方面的缺点：首先，其频率准确度稍差，比铯钟相差一个数量级（铯钟为10-13量级）；其次，铷钟的开机频率复现性不好；第三，其频率漂移率较大，为10-14/d量级（开机阶段和平衡阶段为10-13/d）；第四，铷钟长期频率稳定度随着无规噪声的影响而恶化。这些因素都会影响导航卫星的定位精度[2-3]。为了提高星载铷钟的导航应用能力，需要在保证其短期频率稳定度的基础上，降低频率漂移的影响。由于铷钟频率漂移具有非线性特征，采用线性漂移修正方法不能完全达到目的，需要根据铷钟频率漂移的特征开展工作，本文对实际工作的铷钟特征进行具体分析，研究频率漂移修正的方法，以期找到合理的途径，从而充分地发挥铷钟在导航定位中的作用。

1 铷钟漂移的特征

铷钟开机后，其输出频率随时间的变化与具体的设计和环境因素有关，但总的趋势基本相似[4-5]。图1为某星载铷钟开机后输出频率随时间的变化过程，开始阶段频率向正向漂移（漂移率为10-13/d水平），经过约两天以后，漂移逐渐从正向变为负向，趋于稳定漂移阶段（-10-13/d），之后随开机时间的延长，漂移逐渐减小（小系数10-14/d）。铷钟频率漂移对导航和守时的精度影响很大。

如果是线性漂移，对时间精度的影响可用式（1）来表示[6]：

式中：ΔT为时间误差；α为频率漂移率；t为时间校准间隔。

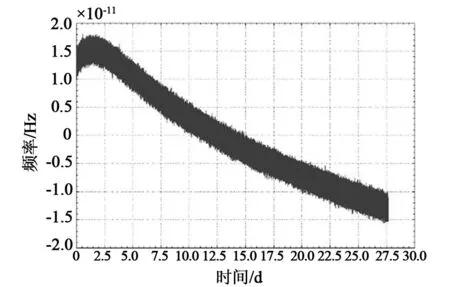
图1 星载铷钟开机后输出频率随时间的变化曲线Fig.1 Frequency curve of rubidium clock on poweron period

由时间误差引起的导航定位误差可以用时差乘以光速来估算，ΔL=cΔT。若取铷钟天漂移典型值为5×10-14/d，按每天校时一次计算，导航定位精度误差估计约为0.65 m。如果将铷钟漂移率修正为5×10-15/d，则其在同等校时间隔内对导航定位精度的影响可以降低一个数量级；在保持同样导航定位精度的情况下校时间隔可以延长两倍以上。时间同步信号如果来自于地面站，需要耗费星地数据链路带宽和通信资源，而且会受到电离层对信号传输的影响。我国的星载铯钟即将搭载升空，将铷钟的频率漂移与星载铯钟的进行比较并加以修正，不仅可以实现精确导航，而且可以借助铯钟长期频率稳定度好和漂移率低的特性，实现长时间的无地面干预自主导航。

在铷钟稳定工作阶段，可以根据铷钟漂移的非线性特征，采用多项式进行频率预估和漂移修正。通常在短时间用二次多项式近似，这时变化趋势可用式（2）表示：

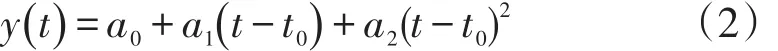
式中：y(t)为t时刻的相对频差；t0为计时起点。设â0、â1、â2为模型参数a0、a1、a2的估计值，可以利用已有ti时刻的测量数据yi进行最小二乘法求出模型参数估计值，并在此基础上进行后期频率预估。计算可用式（3）：

也可用矩阵表示：

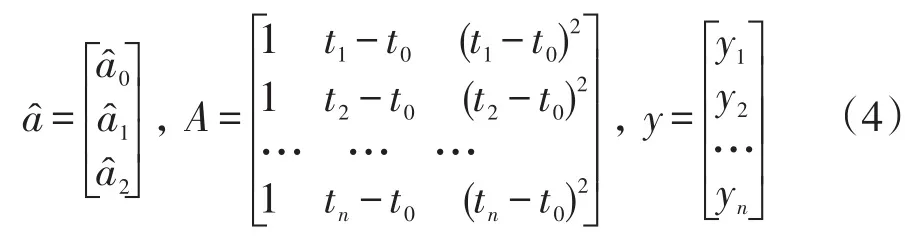
拟合系数可表示为：

图2显示利用Matlab工具对一个铷钟的测试频率数据进行漂移二次多项式修正的结果[7]。根据频率的变化可以计算出其105s取样时间的Allan方差、Hadamard方差（漂移为-10-13/d）和计时时间为天的时间误差分别为8.8×10-14、5.81×10-15和5.17×10-9s；经频率漂移修正后三者分别为8.29×10-15、5.68×10-15和3.12×10-10s。可以看出，漂移修正后的频率曲线较为平直，计时时间为天的时间误差估计精度提高了一个数量级，有利于提高导航定位的精度。但是这种修正方法会受到频率不规则变化的影响，尤其是在铷钟开机阶段和波动阶段表现比较明显。以图1铷钟为例，经二次项频率漂移修正的结果如图3所示（为了显示明显起见，频率数据进行了垂直整体偏置）。拟合结果剩余频率偏差较大（尤其是初始阶段，表现为拟合曲线不平直），这主要是初期频率漂移变化较大和数值由正变负所引起。为了减小二次多项式修正的偏差，可以采取分段修正的办法，但是在分段处会出现较大的误差。

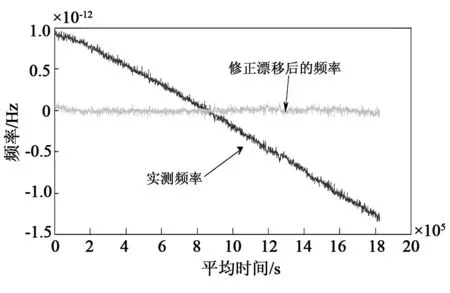
图2 铷钟漂移修正前后频率比较曲线Fig.2 Comparison of frequency of rubidium clock before and after drift correction

图3 铷钟开机和波动情况下的漂移修正效果曲线Fig.3 Drift correction effect of rubidium clock under the condition of start-up and fluctuation

图4给出了在开机后5×105s时分两段二次项拟合结果，可以看出，在分段处拟合曲线有较大波动。同时在拟合曲线两端也有偏离二次项拟合的现象，表现为拟合残差曲线上翘。为了提高精度，可以增加分段值。结合铷钟开机后的频率变化特征，大致分为预热过程、平衡过程和稳定工作过程。这样将漂移补偿过程也分为三段进行。预热过程频率漂移修正时间间隔缩短，以便跟上频率漂移的变化；平衡过程间隔适当延长，以适应导航需求；稳定工作过程频率修正时间可以更长，以保障导航系统的稳定性。但无论如何划分修正时间间隔，在接续点都会出现频率波动，对总体频率变化有较大的影响。考虑到划分越精细，频率修正的量值越小，也可以将分段值设为与测试数据数量相等，随时进行频率修正，这就是Kalman滤波[8]的思想。

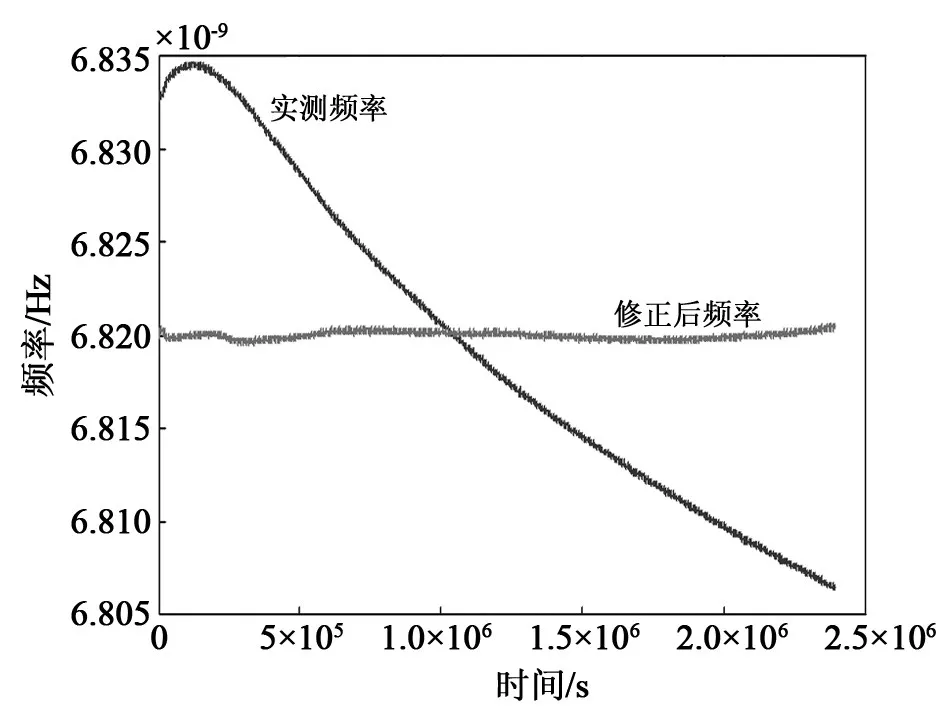
图4 铷钟漂移分段修正效果曲线Fig.4 Subsection correction effect of rubidium clock drift

Kalman滤波的方法是将频率和漂移率作为二维待估计向量x，测量值z为频率偏差，进行最小频率偏差估算和预测。递推公式如式（6）：

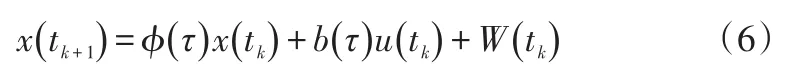
式中：x(tk+1)为时刻tk+1的估计值；φ(τ)为转移矩阵；x(tk)为tk时刻值；b(τ)u(tk)为控制量；W(tk)为过程噪声，τ为时间分步间隔。为调节量。表示过程噪声均值为0，方差为Q：

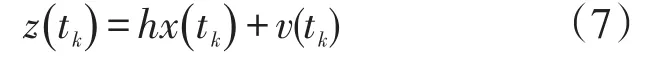
其中，v(tk)～N(0,R)，v(tk)为测量噪声，均值为零，方差为为测量矩阵。

在开始阶段，Kalman估计会随着初始条件的设定而产生不同的数据波动，之后进入稳定状态。这种少数波动不影响整体频差估计效果。如果初始频率和频率漂移设定与实际测量结果相近，则该波动较小。图5为采用Kalman递推的结果，可以看出，经Kalman滤波方法获得的频率残差曲线平直，没有大的波动和固定变化趋势，显示出其普适的拟合与预估能力。

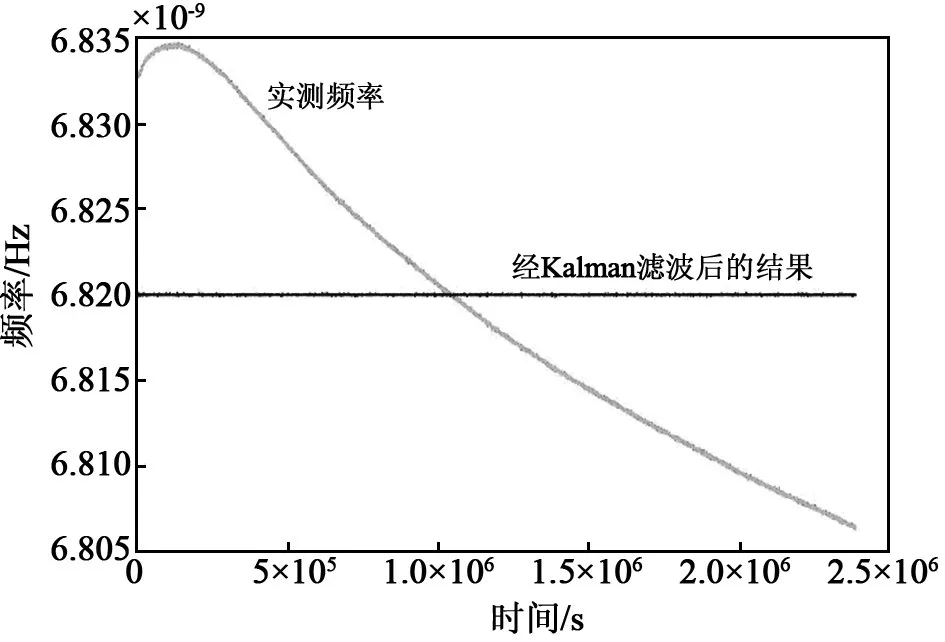
图5 Kalman滤波频率拟合结果Fig.5 Kalman filter frequency fitting results

2 铷钟频率漂移修正需要考虑的因素

修正铷钟频率漂移，首先考虑的因素是频率漂移随时间的变化趋势。短期内铷钟的频率漂移是存在波动的，长期看铷钟的频率漂移具有固定趋势。图6为2015-2018年全球GPS系统上原子钟的漂移变化。追踪铷钟的工作过程，其漂移从10-13/d逐渐降低为小系数10-14/d。在此过程中有小幅波动现象，需要在漂移修正过程中加以考虑。漂移的长期变化可以利用适当的数学模型修正。如果一次修正仍然有固定趋势剩余，可以采用多次修正的办法。经过对GPS星载铷钟的研究发现[9]，铷钟在轨工作500 d以后，进入稳定漂移阶段，可以利用数学模型进行较为完全的修正。在此之前，铷钟的漂移变化相对较快，需要进行实时的修正，以满足导航定位需求。最好的方法是对铷钟的漂移进行预估，这样对时间的保持有利。预估的方法有多种，例如最小二乘法、Kalman滤波和灰度滤波等方法[10]。最小二乘法线性回归计算需要确定回归的时间长度，时间过长会影响回归的线性度，过短会影响回归的准确性，这与标准频率信号的品质和测试系统的噪声相关。若以铯钟作为参考源进行铷钟漂移修正时，由于铷钟的短稳优于铯钟，在漂移率确定过程中需要重点考虑铯钟噪声对结果的影响。铯钟的噪声主要由白频噪声和频率闪变平台构成，假定铯钟的频率稳定度可以用式（8）表示[11]：

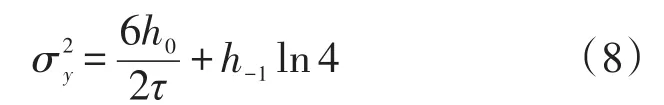
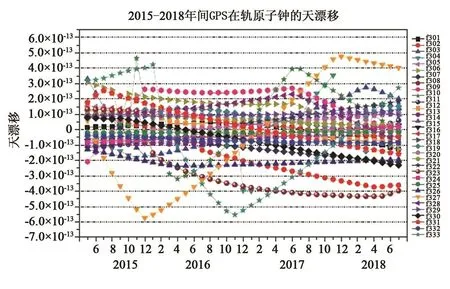
图6 2015-2018年全球GPS系统上原子钟的漂移变化曲线Fig.6 The daydrift of atomic clocks on board GPS in 2015 and 2018

由此引起的漂移率测试方差与测试时间T有关，测试时间越长，精度越高，方差可以用式（9）表示：

目前典型的地面铯钟的短稳指标水平为≤1×10-13@1 s，闪变本底为10-14，能够测出漂移的方差值，如表1所列。

表1 测量时间与漂移率测量误差关系Tab.1 Relationship between measurement time and drift rate measurement error

从表1中看出，在不考虑测量系统噪声的条件下，测试频率漂移率为3×10-14/d的铷钟需要3 d时间。准确修正到小系数10-15量级需要20～30 d的测试时间，修正到小系数10-16量级需要100 d的数据。因此对于铷钟初期漂移可以在开机3天后进行修正，准确修正需要再等待10 d左右，之后可以根据情况间隔20～30 d实施一次。这样由漂移引起的时间误差对导航定位精度的影响由式（1）估算可以减小到厘米量级。实际情况要复杂的多。例如测试系统的噪声和信号传输的噪声需要被考虑，如果测试的是时差，需要将Kalman滤波向量在频率、漂移的基础上增加一个时间（相位）量[12-13]。从自主导航的需求考虑，如果能够将星载铯钟和星载铷钟形成组合钟搭载于导航卫星上，利用比相仪进行比对，通过算法，实时对铷钟的输出频率漂移修正，将铷钟短期稳定度与铯钟的长期稳定度和低漂移结合，不仅可以保证导航和测速的需求，而且可以实现自主导航[14-16]。

3 结论

星载铷钟短期频率稳定度不断提高，已经达到小系数10-13水平，频率漂移对铷钟性能的制约就越发明显。随着对自主导航的迫切需求，修正铷钟的漂移是铷钟应用成败的关键。我国的星载铯钟即将入役，以星载铯钟为参考源对铷钟进行在轨频率漂移实时修正成为可能。本文针对具体的铷钟频率漂移变化规律和铯钟输出频率特征，提出了组合两者优势的铷钟频率漂移修正方法。铷钟和铯钟的组合将在导航卫星系统中更好地发挥作用。