微通道正弦型底面结构对局部流动和传热特性的影响

胡振俊 ，艾 鑫，冯振飞 ，2

（1.广西大学机械工程学院，南宁 530004；2.广西大学广西石化资源加工及过程强化技术重点实验室，南宁 530004）

0 引言

在航空航天、制冷等诸多工业领域中，设备在工作时往往产生大量的热量，因此需借助散热器进行冷却，以确保其能够在可靠的工作温度下运行。随着科学技术的不断进步，各种设备向着集成化和微型化方向发展，然而由此引起的高热通量散热问题却制约着其进一步发展。为了有效地解决此问题，工程师们一直致力于散热器的研究和改进工作。1981年，Tuckerman等[1]设计出一款微通道散热器，该散热器具有传热系数高、冷却效果好、体积小、质量轻和工质充注少等优点[2]。鉴于此，微通道散热器自提出以来，一直受到学者们的青睐，并进行相关的研究和改善，以进一步强化传热性能。在强化传热问题上，由于被动传热不需要额外的能量（泵功除外），因此该方法成为了强化微通道传热的重点研究方向之一。

众多的被动传热方法中，在微通道内增加凹穴、内肋、凸起物等凹凸结构以增强流体扰流的方法是研究的重点之一。冯振飞等[3]发现螺旋通道中的凹穴增加了流动阻力但对传热几乎没影响，而直通道凹穴对流动和传热影响明显。Pan等[4]实验研究了扇形凹穴型微通道换热器传热特性。夏国栋等[5]研究了具有内肋的凹穴通道，结果表明凹穴对熵产影响不大，而内肋的影响较大。贾玉婷等[6]对水滴型凹穴通道进行数值模拟研究，发现其结构使得局部压降呈锯齿形下降，在凹穴处会产生漩涡，从而使得传热效果得到强化。Chai等[7]从局部的流动和传热方面分析了不同凹凸结构的三角肋片传热特性。张弛等[8]探究了以硅为材料的正弦型波纹通道不同波长和相位对流动和传热性能的影响。Shen等[9]研究了错列布置的逆流波纹双层微通道散热器对流换热，结果表明交错排列结构的热性能比平行排列的好，并且没有明显的压降损失。Dharaiya等[10]采用数值模拟方法对微尺度下通道内正弦型结构流动和传热性能进行分析，并建立了一个数值模型来预测光滑通道和表面粗糙通道中流体流动特性的影响。Hamidreza等[11]通过对正弦型结构参数和雷诺数对超疏水材料的微通道摩擦阻力系数和努塞尔数影响的研究发现，用超疏水壁面代替传统材料的壁面后，摩擦阻力系数和努塞尔数均有所降低。

从上述的研究文献中可见，学者们在研究凹凸结构对通道传热性能的影响时，热衷于研究凹凸结构设在两侧壁面的微通道，而对设在离热源最近的底面的微通道研究较少，尤其是对正弦型底面的微通道鲜有研究。此外，这些研究往往更关注的是整体的流动和传热性能，而对利于发现其内在规律的局部流动和传热性能关注不足。鉴于此，本文以正弦型底面的微通道结构为研究对象，采用数值方法对局部流动和传热性能进行研究，分析其内在的流动和传热规律，进而揭示其传热强化机理。

1 模型描述

1.1 物理模型

本文研究的正弦型微通道模型如图1所示。该模型宽W=1 mm，长L=40 mm，高H=1.5 mm。模型顶部与绝热的盖板接触，形成微通道。通道内尺寸宽Wch=0.5 mm，高Hch=1 mm，由Dh=2WchHch/（Wch+Hch），可得到水力直径Dh=0.667 mm，半肋宽a=0.25 mm。通道的底面为正弦波面，波面总长l=30 mm。入口和出口两端分别设置长度为5 mm的光滑面，利于流体进入波纹段通道和防止出口回流现象。为了解正弦型底面结构对微通道的流体流动和传热性能的影响，通过改变正弦曲线的波长λ和振幅A，设计了5种不同类型的正弦型微通道模型。将这5种模型分别进行命名：MC-0.1-2（A=0.1 mm，λ=2 mm）、MC-0.2-2、MC-0.3-2、MC-0.2-1、MC-0.2-5。此外，还模拟了光滑微通道（MC），作为流体流动和传热性能优劣比较的基准。

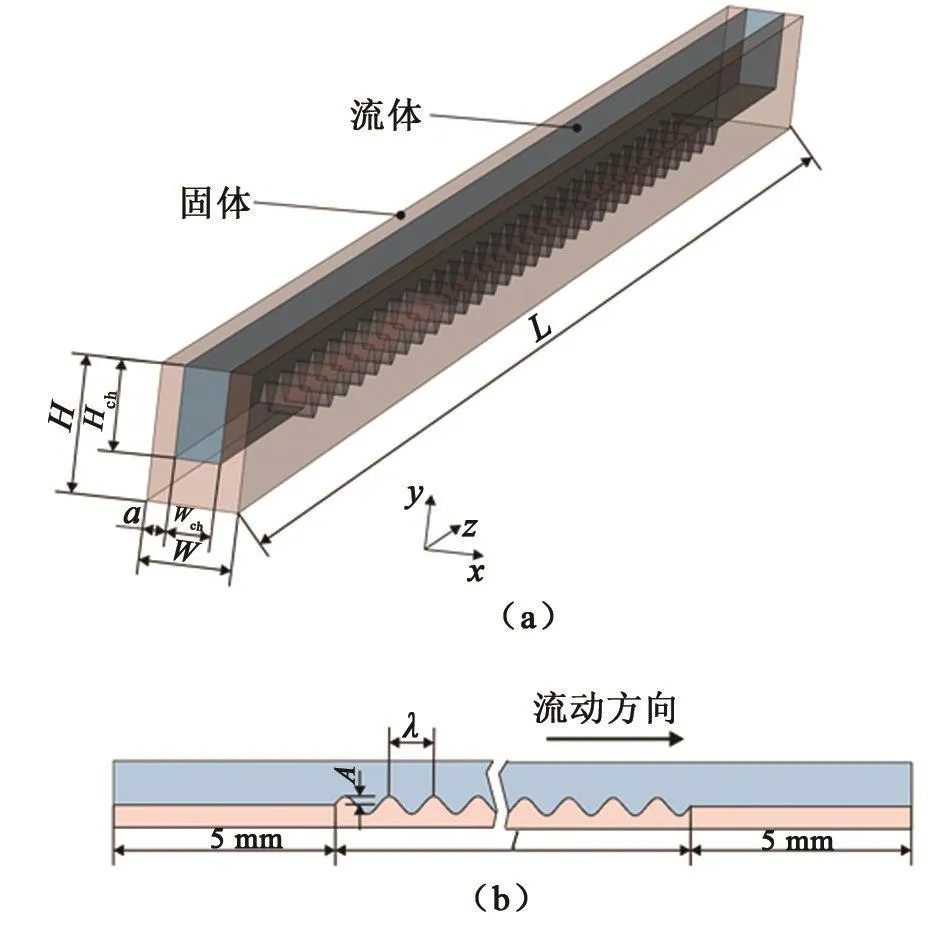
图1 正弦型微通道模型Fig.1 Sinusoidal microchannel model

1.2 数值模型

由假设可以得到连续方程、动量方程和能量方程分别为：

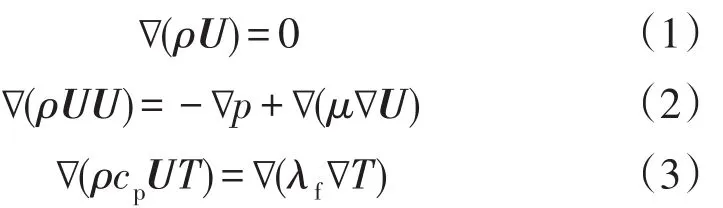
由于固体域没有流速，其U=0，故只需分析其传热，能量方程为：

式中：Ts、Tf分别是固体域和流体域温度，K；ρ为流体的密度，kg/m3；μ为粘度，Pa·s；cp为比热容，J/（kg·K）；p为流体内部压力，Pa；λs和λf为固体域和流体域导热率，W/（m·K）。

模型采用恒速度和温度进口边界条件，入口速度uin为0.4～1.6 m/s，由式（5）得到的雷诺数为230～1 060，入口温度Tin=293 K。出口处设置相对出口压力pout=0 Pa（相对于环境）。模型底面为恒热流加热，热流密度q=400 kW/m2。模型两侧设为周期循环边界条件，流体域和固体域交界处设为固液交界面，模型的顶部表面和其他面均设置为绝热面，计算的收敛残差设为10-5。

式中：ρin为进口流体密度，kg/m3；μm为流体质量平均粘度，Pa·s。

在数值模拟前，对模型进行网格划分，鉴于结构网格具有更高的网格质量，因此采用结构网格进行划分。选取结构MC-0.1-2为例进行网格验证，取网格数分别为106.4万和219.3万的模型与321.0万的进行比较。当雷诺数为530时，其压降误差分别为2.00%和0.77%，表明取网格数为219.3万时的计算结果是符合网格无关性要求的，因此取该网格数进行计算，即能节省计算时间，又能保证结果的合理性。MC-0.1-2的最终网格结构如图2所示。

2 结果分析

2.1 沿程摩阻系数和努塞尔数计算

流体沿着z轴方向的局部摩擦阻力系数fz及平均摩擦阻力系数fave计算如下：

门诊癌痛和慢性疼痛患者信息化管理平台的建立与实践…………………………………………………… 龚晓英等（4）：450

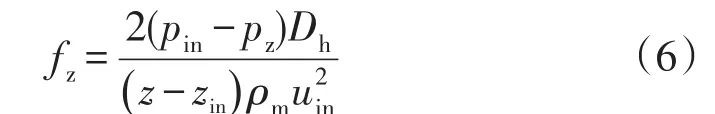
式中：zin为进口的z坐标，mm；pin和pz分别是进口和给定z坐标截面的质量流量平均压力，Pa；Δp为通道进出口压降，Pa；ρm为体积平均的密度，kg/m3。

图2 MC-0.1-2的网格结构图Fig.2 Grid structure of MC-0.1-2

流体局部努塞尔系数Nuz及平均努塞尔系数Nuave计算公式为：

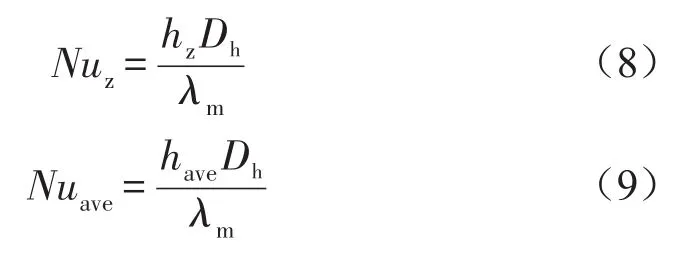
式中：λm为质量平均的导热率，W/（m·K）；hz和have分别为给定z坐标的局部传热系数和整个通道的平均传热系数，W/（m2·K），其计算公式如下：

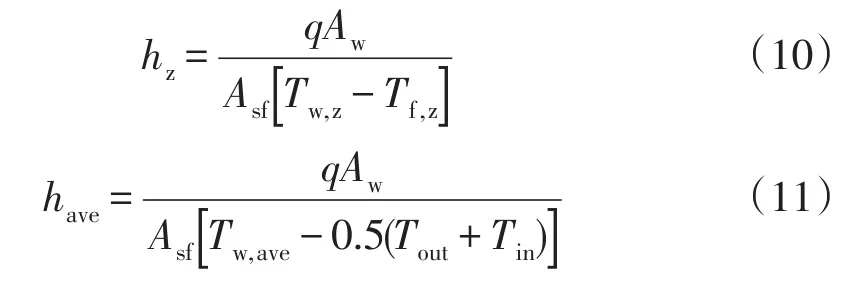
式中：Aw和Asf分别为通道加热底面和固液交界面面积，m2；Tw，z和Tf，z分别为给定z坐标的局部壁面平均温度和流体平均温度，K；Tw，ave为平均壁面温度，K；Tout为出口处的流体平均温度，K。

2.2 数值模拟有效性验证

将光滑通道进出口压降和温差的数值模拟结果与理论计算结果进行对比，以验证本文所采用的数值计算方法的有效性。根据文献[13]给出的关于光滑矩形直通道的理论计算压降公式为：

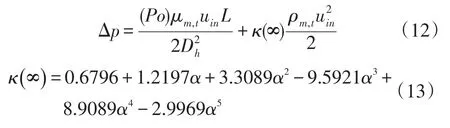
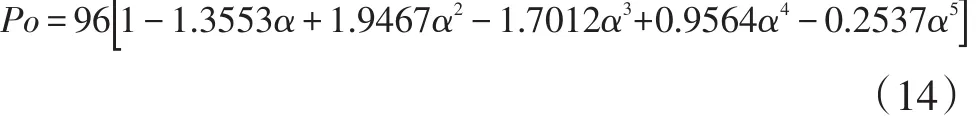
式中：Po为泊肃叶数；κ（∞）为Hagenbach修正系数；α为通道横截面的宽高比；ρm，t和μm，t分别是平均流体温度下的密度和粘度，当q=0 W/m2时，流体温度为293 K，因此其值分别为998.2 kg/m3和0.001 004 Pa·s。

理论进出口温差的计算见参考文献[14]，根据能量守恒，得出通道进出口温差的理论公式为：

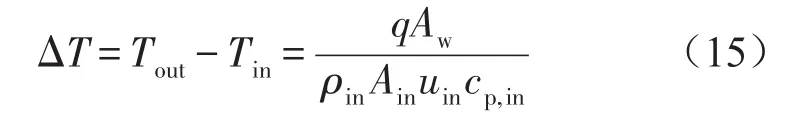
式中：Ain为进口横截面面积，m2；cp，in为进口流体温度对应的比热容，J/（kg·K）。

图3给出光滑通道MC进出口压降和温差的模拟值与理论值的比较。可以看出，模拟的压降和温差与理论值吻合较好，曲线趋势变化比较一致，最大误差分别为4.59%和1.85%，表明本数值计算所用的方法有效。

图3 光滑微通道MC进出口的压降和温差的模拟值与理论值的对比曲线Fig.3 Comparisons of simulation data with theoretical data for pressure drop and temperature difference in a plain microchannel

为了进一步验证本数值方法的有效性，基于文献[15]的实验模型（正弦微通道MCH-15）建立了相同的几何模型，并采用本数值方法进行计算。计算结果与文献[13]的实验结果进行对比，如图4所示。可以看出，压降的模拟值和实验值趋势一致，最大误差为17.2%，平均误差为7%，从而进一步验证了数值模拟的有效性。

2.3 局部流动分析

图5是雷诺数为1 060时，各微通道内速度场和速度矢量的分布图。为方便对比分析，固定速度为0～4 m/s。从图中可以直观地看出：（1）光滑矩形微通道流速最大在中心处，且速度分布均匀规则；（2）正弦型微通道在凹穴处出现了速度方向与主流方向相反的现象，说明在该处产生了二次流；（3）MC-0.2-2和MC-0.3-2在底面近壁面处流体在冲击壁面时回流速度较大，二次回流效果较为明显，而其他结构的二次流效果较弱；（4）MC-0.2-2和MC-0.3-2在底面近壁面处流体在冲击壁面时回流速度较大，能更好地混合冷热流体，提高传热性能，而其他正弦型凹面的二次流效果并不明显，速度较慢，有可能导致在该处形成滞留，恶化传热效果。

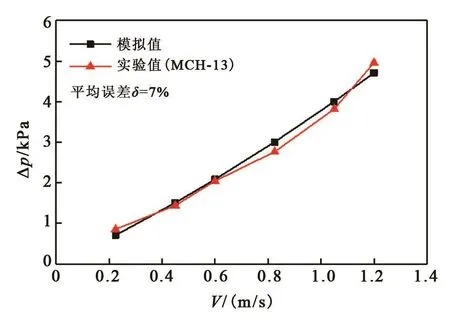
图4 正弦型微通道压降随速度变化的模拟值和实验值对比Fig.4 Comparison of simulated and experimental values of pressure drop with velocity in sinusoidal microchannels

图5 雷诺数为1 060时局部流动速度场分布图Fig.5 Local flow velocity distribution at Re=1 060

图6 是雷诺数为530和1 060时，不同结构下微通道的局部压力沿着流动方向z变化的情况。可以看到，正弦型微通道压力先沿着z轴平滑下降，而后呈现波浪状下降趋势。这是因为正弦底面微通道前有5 mm的光滑过渡段，因此压力趋势呈现出平滑的曲线。流体通过正弦底面后压力产生了波动，由伯努利效应可知，在正弦曲面的凸面，流体流过的面积减小，流速增大，静压力降低；在正弦曲面的凹面，流体流过的面积突然增大，流速减小，静压力升高。流体流过正弦曲面的凹凸面，使得局部静压力呈现周期性波动。由图还可知，当雷诺数为1 060时，在距离通道出口5 mm处，产生了较为明显的压降，甚至出现了负压，其中MC-0.3-2尤为明显。这是因为流体在经过正弦曲面和光滑面交界处时产生了剧烈的回流，形成漩涡（如图7所示），使得在该处的逆向压力梯度大于正向压力梯度，导致该处出现了负压。而当雷诺数为530时这种效果并不明显，说明在该雷诺数下流体运动相对平缓。

图6 雷诺数为530和1 060时沿程压力分布图Fig.6 Pressure distribution along flow direction with Reynolds numbers of 1 060 and 530

图7 MC-0.3-2的压力云图及速度矢量图（Re=1 060）Fig.7 Pressure distribution and velocity vector of MC-0.3-2（Re=1 060）

图8 是不同结构下正弦曲面微通道的局部泊肃叶数fzRe沿流动方向z/L变化的趋势。可以看出，泊肃叶数随着z/L的增大而减小，光滑通道MC平滑下降，而正弦型通道则呈现规律性波动下降，但其整体泊肃叶数比光滑通道大，说明正弦型曲面增大了通道的摩擦阻力系数。在本研究的范围内，将正弦型底面的通道MC-0.2-2、MC-0.1-2、MC-0.3-2进行对比可知，正弦型底面振幅A越大，泊肃叶数越大，即对应的摩擦阻力系数就越大；对比正弦型底面的通道MC-0.2-1、MC-0.2-2和MC-0.2-5可知，波长λ越小，泊肃叶数越大，即对应的摩擦阻力系数就越大。综合图的趋势来看，模拟的5个结构中，振幅A对摩擦阻力系数影响最大，而波长λ影响较小。

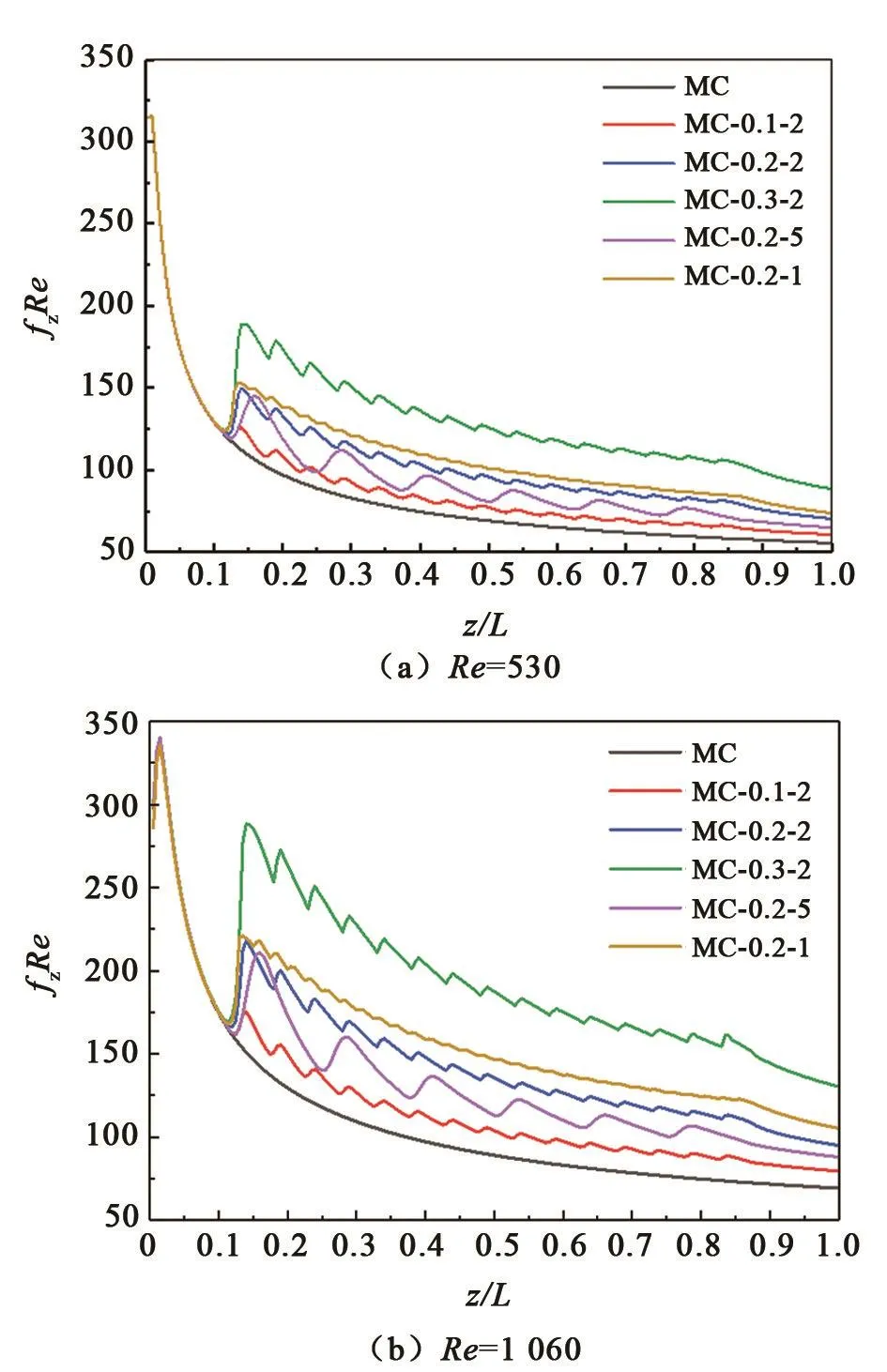
图8 不同结构的局部泊肃叶数沿流动方向的变化曲线Fig.8 Variations of local Poiseuille number of different structures along flow direction

图9 是平均泊肃叶数faveRe随着雷诺数变化的趋势。可以看出faveRe随着雷诺数的增大而增大，正弦型通道的faveRe大于光滑通道。对比MC-0.2-2、MC-0.1-2、MC-0.3-2可知，正弦型底面振幅A越大，faveRe越大；对比MC-0.2-1、MC-0.2-2和MC-0.2-5可知，波长λ越小，faveRe越大。这与图8局部分析所得结论一致。

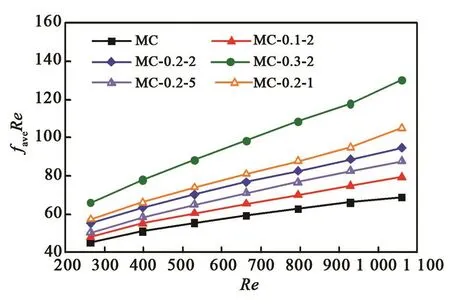
图9 平均泊肃叶数随着雷诺数变化的趋势Fig.9 Variations of average Poiseuille number with Reynolds number

2.4 局部传热分析

图10 给出了不同微通道结构的纵截面温度场分布。图11给出了光滑通道与MC-03-2通道在z=20.5 mm处横截面的温度场分布。

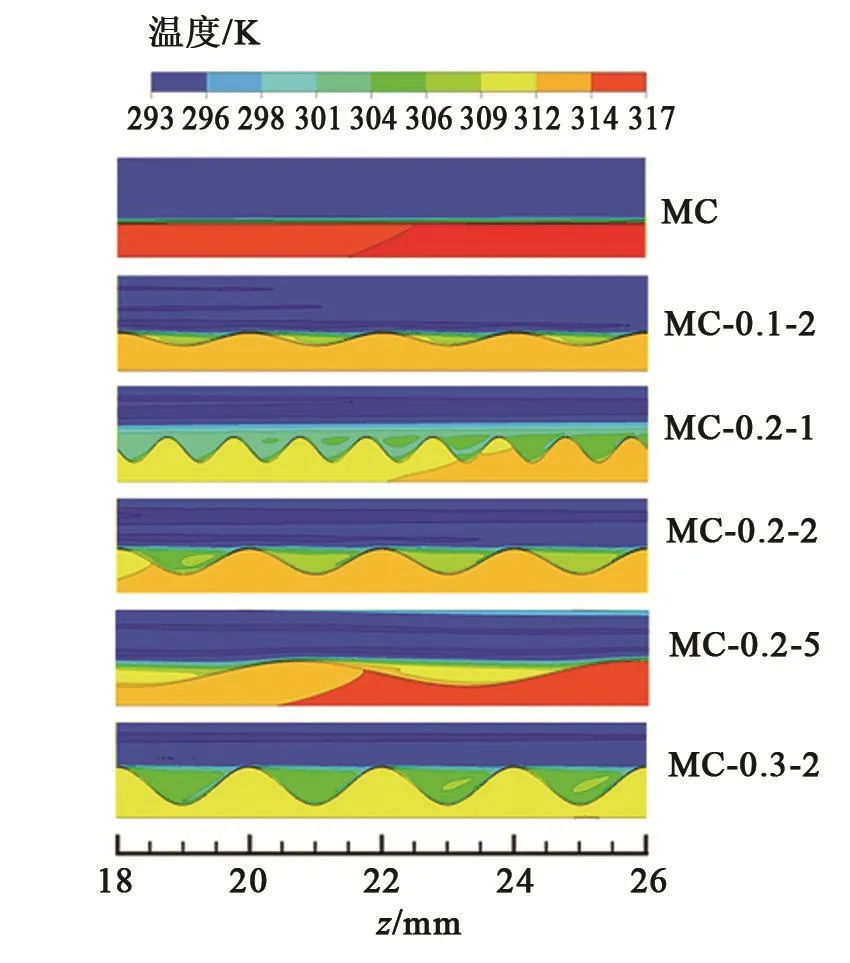
图10 不同微通道结构的纵截面温度场分布（Re=1 060）Fig.10 Temperature distribution in different microchannel structures（Re=1 060）

从图10和图11中可以看出：（1）光滑矩形通道的固体域温度相对于正弦型通道略高一些，表明正弦型底面通道换热效果好于光滑矩形通道。结合图5可知，正弦型通道内的流体会出现二次流，有利于冷热流体的混合，使得传热得以强化，因此固体域温度会下降。（2）光滑矩形通道热边界层较薄，分布均匀，而正弦型通道热边界层较厚，因此换热效果较好。（3）流体经过正弦型通道凹面时，有部分流体在凹面处形成温度较高的闭合面流体，这是因为流体在凹面处流动过程中，沿着壁面的流体速度较快，中心处速度较低，使其形成漩涡，使得流体带走的壁面温度在中心处集中，导致中心处温度偏高。

图11 光滑通道与MC-03-2通道在z=20.5 mm处横截面的温度场分布（Re=1 060）Fig.11 Temperature field distribution of cross section at z=20.5 mm of smooth channel and MC-03-2 channel（Re=1 060）

图12 是雷诺数为530和1 060时，壁面温度Tw，z随着z轴变化的曲线。从整体上看，壁面温度随着z坐标先增大而后平缓。当雷诺数为1 060时，正弦型微通道的壁面温度远小于光滑微通道MC的壁面温度，而在雷诺数为530时，两者的壁面温度变化不大。这说明在雷诺数Re=1 060情况下，正弦型底面结构能使换热得到有效强化，但在雷诺数Re=530时，强化效果并不明显。这是由于在雷诺数为1 060时，流速较快，流体冲击壁面更剧烈，产生更明显的二次流，使得冷热流体充分混合，并且不断地打断边界层，使换热效果得到明显改善；在雷诺数为530时，流速较慢，流体通过凹穴底面时，流速更慢，使得在凹穴处二次流微弱，甚至发生滞留现象，导致传热效果恶化。

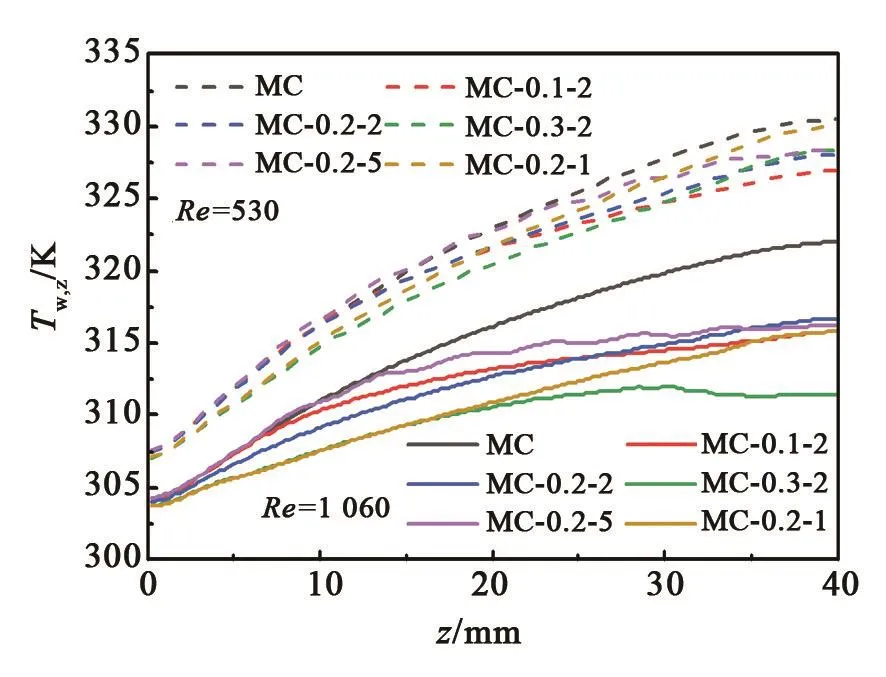
图12 雷诺数为530和1 060时壁面温度随着z轴变化的曲线Fig.12 Variations of wall temperature with z axis at Reynolds numbers 530 and 1 060

从局部上看，Re=1 060时，微通道MC-0.3-2壁温下降明显，说明其结构换热效果表现最好，而微通道MC-0.2-5，表现较差，甚至在距离进口5～15 mm处，出现了壁面温度比光滑曲面高的现象，这说明该结构在此处传热效果出现了恶化。综合分析可见，雷诺数为1 060时，在所研究的结构范围内，正弦通道的振幅越大或波长越小，传热效果越好；雷诺数为530时，正弦通道的振幅和波长对壁面温度的影响没有明显线性规律。

图13为不同结构的局部努塞尔数Nuz随着流动方向z/L变化的曲线。可以看出，努塞尔数沿着z/L呈下降趋势。在入口处，由于入口效应的影响，努塞尔数稍微增大；在出口处，由于材料导热作用，通道的最高温度并不在出口处，使得努塞尔数在末端出现轻微上扬。对比分析两图可知，雷诺数为1 060的正弦型微通道努塞尔数比光滑通道提高明显，而雷诺数为530时的正弦型微通道努塞尔数和光滑通道比提高不大，甚至有小于光滑通道努塞尔数的情况。这说明，雷诺数为530时，正弦型微通道并不能使流体产生有效扰动，反而造成通道内流体发生滞留，恶化传热。综合来看，当雷诺数为1 060时，MC-0.3-2平均努塞尔数最大，说明传热效果最好，而MC-0.2-5传热效果最差；雷诺数为530时，MC-0.3-0.2和MC-0.1-2平均努塞尔系数较大，传热效果较好，而MC-0.2-1平均努塞尔数最小，传热效果最差。整体分析可知，在雷诺数为1 060时，正弦型微通道努塞尔数随波形的幅度增大而增大，随波长增大而减小。

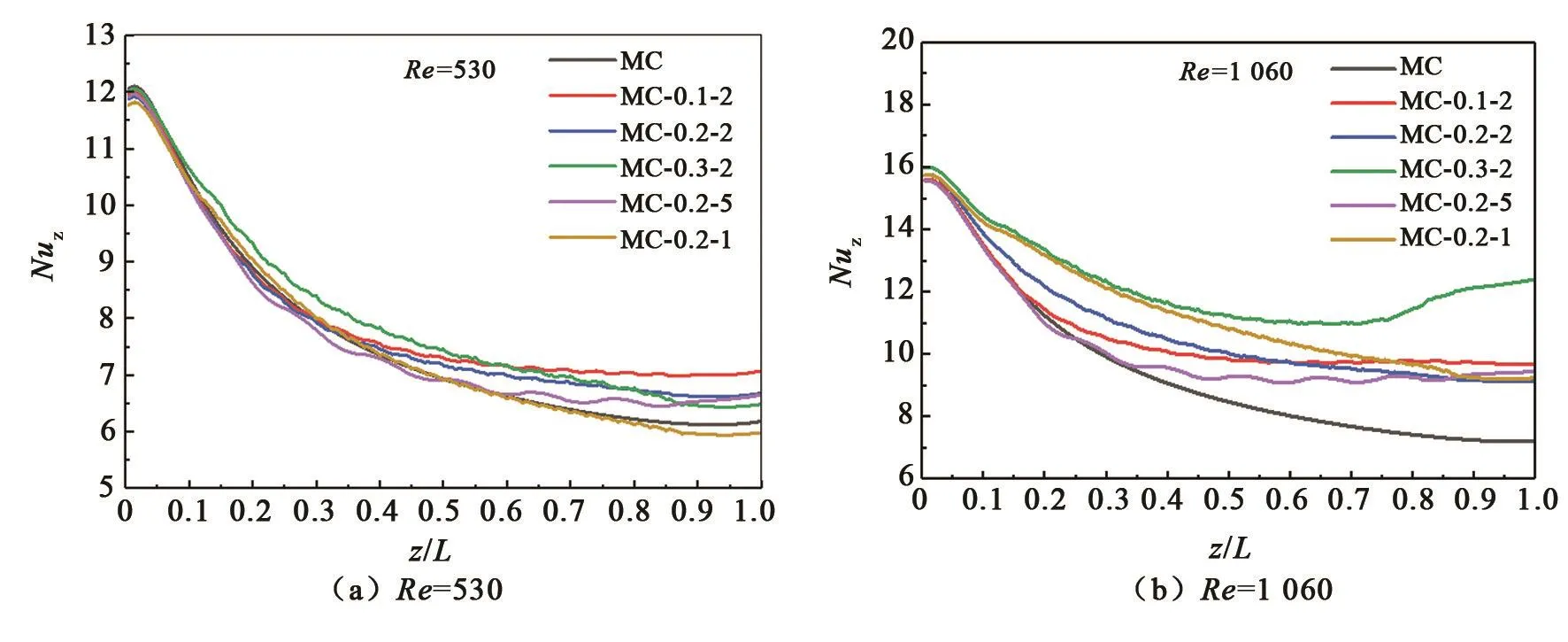
图13 不同结构的局部努塞尔数随着流动方向变化的曲线Fig.13 Nu z of different structures change with flow z/L

图14 为平均努塞尔数Nuave随着雷诺数Re的变化趋势图。

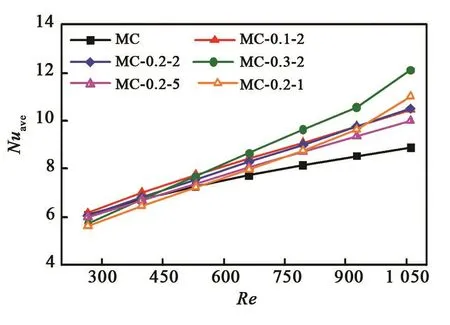
图14 平均努塞尔数随着雷诺数的变化趋势Fig.14 The variation trend of Nu ave with Re

由图14可以看出，正弦型结构微通道在雷诺数不大于600时Nuave和光滑通道MC的Nuave相比相差不大，甚至有低于光滑通道Nuave的情况，说明传热效果略差；而在雷诺数大于600时，正弦型微通道的Nuave增大比较明显，传热效果较好。

3 结论

为研究微通道的正弦型底面结构对流动和传热性能的影响，本文设计了5种正弦型底面的微通道，并采用数值方法研究了雷诺数为230～1 060时的局部流动情况和传热性能。结论如下：

（1）正弦型微通道存在二次流现象，使得其温度场相对于光滑通道发生改变；在雷诺数较高时，MC-0.3-2通道的二次流效果最明显，对应的壁面温度也明显下降。

（2）正弦型微通道压力和壁温沿着流动方向的趋势分别是逐渐减小和增大；两种趋势都出现波动，且其幅度和波长与正弦型底面的波形相对应，但壁温的波动平缓些。

（3）正弦型微通道的局部泊肃叶数和努塞尔数沿流动方向的趋势在正弦型底面的通道段出现波动，但后者波动平缓些；雷诺数为1 060时，正弦型底面的振幅越大或波长越小，局部泊肃叶数越大，即摩阻系数也越大，但振幅的影响更显著；局部努塞尔数也有相似的规律。

（4）正弦型微通道在雷诺数不大于600时Nuave值与光滑通道的Nuave相差不大，甚至有出现Nuave的值小于光滑通道的情况，表明传热效果略差。而在雷诺数大于600时，正弦型通道的平均努塞尔数大于光滑通道，表明正弦型微通道在雷诺数大于600时传热强化的效果更好。