铯束管的出气率模型及应用

陈 江，杨 斓，成大鹏，郭美如，杨 军，刘志栋，马寅光，黄良育

（1.兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000；2.空军研究院系统工程研究所，北京 100076）

0 引言

铯束管是铯原子钟的物理部分，原子钟跃迁信号在其内部产生[1-2]。铯束管需要提供一个真空度优于1×10-4Pa的环境[3]，以保证原子跃迁信号的信噪比超过2 000（1/4 Hz）。

对于可搬运的铯束管，为了长期维持内部的高真空，一般将其密封，并内置小钛泵。然而管内的出气源很多，来自不同材料，如石墨、陶瓷、聚酰亚胺、1J85、各种磁钢等，这些材料的表面积之和一般在几个平方米，如果不经过特殊处理，从材料表面放出的气体很容易使铯束管的内部压力超过设计要求。因此在铯束管的真空设计中，材料表面的出气率成为优先考虑的因素[3]。

为了使铯束管的材料出气率降低到设计要求，需要对铯束管及各种材料进行复杂的除气处理[4-5]，其中一项处理就是铯束管的烘烤与排气。将铯束管接在真空系统上，从外部对其加热，加速释放出材料内部的气体。考虑到个别材料在超过某一温度时化学性质将发生变化，如聚酰亚胺在接近400℃时将碳化，铯束管的烘烤温度不宜过高。又考虑到铯束管内精密的束光学系统，以及对真空度高低敏感的MgO膜层，升温速率亦不能过大。这一过程中，升温速率不同，材料表面的出气率也将不同。

由于铯束管属于密封结构，所以无法直接测得内部材料的表面出气率。为了解决这个问题，需要建立铯束管的出气率模型。据了解，目前还没有文献报道如何建立该模型。本文提出了一种获得出气率模型的方法，该方法利用了在铯束管烘烤排气过程中从管内排出的气体量等于从材料表面释放出的气体量这一假定，得到出气率与排气系统压力之间的数学关系，即出气率模型。这样，就可以通过真空计读数得到出气率了。

在铯束管排气过程中，另一个困难的问题是如何判定过程是否可以结束（即封离排气系统）。一般是通过经验的方法来判断的，观察真空计读数，当该读数小于某一经验值时认为可以结束。本文将利用模型给出这一方法的理论基础，并给出精确的判定数值。

1 模型的建立

铯束管排气系统属于复杂真空系统，由抽气系统、加热装置、真空规和控制系统等组成，如图1所示。抽气系统由真空泵组、阀门及各种管道组成（如图1虚框），铯束管内部材料放出的气体由其排出。加热装置一般由电加热丝或气体燃烧室、测温探头及控温探头等组成，用于加热铯束管以加速释放出材料内部的气体。控制系统由真空计、加热控温设备及其他相关设备组成，这些设备可采集包括真空规、抽气系统、加热装置在内的测试或运行数据并进行处理，保证整个系统运行正常。

图1 排气系统的组成示意图Fig.1 Composition diagram of exhaust system

建立出气率模型，就是要建立铯束管内材料表面出气率与抽气系统内部压力之间的关系。为此将排气系统简化为如图2所示的结构。该结构由铯束管、排气管道、抽气系统和真空计等四部分组成。结构中略去了加热装置与控制系统，并将真空泵组、阀门与管道在内的整个抽气系统用一个框图代表，真空计和铯束管分别接在抽气系统上。图2中p为抽气系统的压力，S为抽气系统进口处的有效抽速，Q是每秒从铯束管抽掉的气体量。

一般而言，真空系统内材料表面的平均出气率q是随时间t变化的，用式（1）表示[6]：

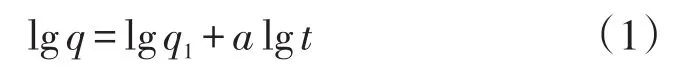
式中：q1为常数；a为出气率的衰减系数，取值在0.5～1之间。对于铯束管，烘烤排气时出气率不仅与时间t有关，也与烘烤温度T有关。假定铯束管内各部件表面积之和为A，那么铯束管内总出气量为q（T，t）A，这部分气体通过排气管道由抽气系统排出。为了建立出气率模型，假定从铯束管排出的气体量等于材料表面的出气量。如若不然，排气管道两端的压力差将增大，从而将加速管道内气体的流动，直到这两个量相等。该假定用数学公式表示为：

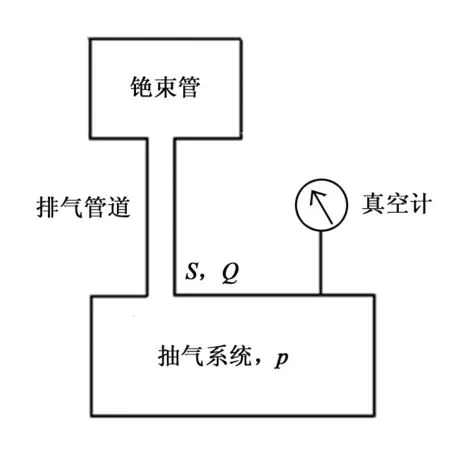
图2 简化的排气系统图Fig.2 Simplified exhaust system

抽气系统未装载铯束管时的极限压力值用p0表示。p0可以这样获得：在抽气系统空载的情况下，经过长时间的抽气，当真空计的读数不再发生变化或变化很小时，该读数就是p0。装载铯束管后，从排气管流入的气体使抽气系统的压力发生变化。根据假定，每秒从铯束管排出的气体量Q全部进入抽气系统，据此可计算出抽气系统装载铯束管后的压力：

将式（3）代入式（2），得：

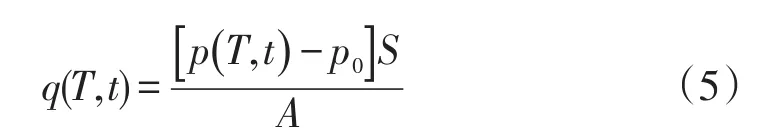
式（5）便是铯束管的出气率模型，式中特别恢复了q和p对T和t的依赖关系。式中的A和S是固定值，分别决定于铯钟管和抽气系统的设计，p0是极限压力，也可认为是固定值。式（5）的意义在于q(T,t)的值完全通过p(T,t)得出，从而使研究铯束管的出气率随温度和时间变化规律变得简单。图3是通过真空计读数获得的不同编号铯束管出气率随时间和温度变化的曲线。据此可以研究铯束管

解出q，得到关系式：的出气率的变化情况，并可以优化升温策略。

图3 铯束管的出气率变化情况Fig.3 Outgassing rate of cesium beam tube

2 模型的应用

出气率模型可以用于判断烘烤完毕的铯束管是否可以封离排气系统。本文针对体积大小为4 L，管内各种材料的表面积之和为3 m2的铯束管叙述应用方法。

根据文献中提出的铯束管真空设计方法[3]，假定铯束管的静态放置时间为1个月，可计算出管内材料的表面出气率应小于q0=5.2×10-11Pa·L/（s·cm2），如果此条件满足，那么在铯束管静态放置不超过一个月的情况下，溅射离子泵可正常启动，铯钟可以正常工作。

为了使出气率小于q0，需要对铯束管烘烤排气。由于烘烤温度不宜过高，所以只能延长排气时间。延长多久取决于铯束管内材料的出气率是否达到设计要求。一般排气系统没有直接测量出气率的设备，只能根据排气系统真空度的经验值来决定是否延长排气时间。这带来两个问题：一是，如果给出的经验值过大，铯束管内部的真空将无法维持；二是，若经验值过小，要付出额外的时间和资源。

利用材料出气率模型可以解决上述问题。由于式（4）与式（5）等价，这里应用式（4）更方便。将q0的值代入式（4），解出对应的压力p′，此值即为当材料的出气率达到设计要求时抽气系统内部应达到的压力。注意这里不涉及温度T和时间t，故不考虑这两个自变量。观察真空计的读数p并与p′比较，如p≤p′，则铯束管可以封离排气系统。

将上述方法应用于某铯束管排气系统，如图4所示。该系统的抽气机组包括机械泵和分子泵，真空计采用了冷阴极电离真空规和分离规。冷阴极电离真空规的测量范围为105～10-7Pa，分离规的测量下限为10-10Pa。系统的极限压力p0为8.0×10-8Pa，直接从分离规获得。根据机械泵和分子泵的抽速、系统管道及铯束管排气管道的尺寸，可以定出系统的有效抽速[7]为S=40 L/s。

根据模型计算该系统对应的p′值。将q0=5.2×10-11Pa·L/（s·cm2）、A=30 000 cm2、p0=8.0×10-8Pa及S=40 L/s等代入式（4），求得p′=1.2×10-7Pa。从冷阴极电离真空规或分离规读出抽气系统的压力p，如果p小于1.2×10-7Pa，排气过程可以结束。

图4 铯束管排气系统Fig.4 Exhaust system of Cesium beam tube

3 总结

通过从铯束管内排出的气体量等于从材料表面放出的气体量这一假定给出铯束管排气过程中材料的出气率数学模型。利用模型，通过观察真空计读数的变化，就可以确定出气率的变化，从而使出气率的研究变得简单。本文还给出了模型的应用，用于判断铯束管完成烘烤后是否可以封离排气系统。根据出气率的设计值，通过模型得到对应的压力值，如果真空计读数小于对应的压力值，说明排气过程可以结束，这样，铯束管封离排气系统的判断便有了依据。