磁场力非均匀度对液氧磁补偿微重力自由界面的影响
张泽宇,黄永华*,梁益涛,耑 锐,张 亮,卜劭华
(1.上海交通大学制冷与低温工程研究所,上海 200240;
2.上海宇航系统工程研究所,上海 201108)
0 引言
在空间微重力环境中,表面张力相对于自然对流占主导作用,因此流体的流动和传热特性与地面常重力条件下存在显著区别,这对低温推进剂的在轨贮存和管理技术等带来了挑战。进行微重力实验的常规研究手段有落塔[1]、抛物飞机[2]和探空火箭等,其中最完美的手段是在空间站等真实微重力场所进行实验。落塔实验通常整个过程都不到5 s,而其他手段费时费力,成本高昂。此外,相比于常温流体,进行低温流体微重力实验挑战性更大。近20年来,磁重力补偿成为这一领域的新方向,特别是物理科学和生命科学实验,如对液氦[3]、液氢[4]、液氧[5]、水[6]甚至玻璃等介质的相关实验。在力平衡理论方面,从麦克斯韦方程出发,引入场向量G=grad(B2)(其中B为磁感应强度)对磁重力补偿的条件进行描述,以便分析磁力场分布特征[7],从而指导所需的磁场设计。特别需要指出的是,由于液氧本身具有顺磁性特征,且其磁化系数高出其他低温流体(液氢、液氮等)几个数量级,同时液氧又正好是低温推进剂的氧化剂,因而最适合用来进行磁补偿微重力实验。
国际上相关研究机构已对低温流体的磁补偿微重力模拟开展了一定的实验研究。如美国国家强磁场研究中心(NHFML)在1999年首先利用超导磁体对直径Φ10 mm的球形区域内进行了0.1 g水平的液氦液滴微重力补偿实验观察[8]。日本筑波大学磁场研究中心于2002年通过数值模拟的方法对超导线圈的结构进行了分析设计,搭建了一套磁补偿微重力实验台,在Φ10 mm×20 mm区域的柱形区域内实现了0.01 g水平的微重力补偿,并进行了水等流体的微重力实验[9]。法国原子能总署(CEA)于2004年搭建了针对液氢的微重力补偿实验台,并对液氢进行了磁补偿微重力环境下临界流动实验[10],而后又对实验台进行了改进,在Φ30 mm×50 mm的柱形区域内达到了0.04 g的微重力补偿水平,并对液氧开展了微重力池沸腾[11]及变重力加速度[12]等相关实验。
由此可见,尽管国外已对低温流体开展了一定的磁补偿微重力实验,但都只能达到0.01 g量级的微重力水平(可能与其所利用的超导磁体结构单一有关),且基本上未涉及对磁场均匀性,特别是关于磁场均匀性是如何影响磁重力补充水平方面的阐述。另一方面,国内在磁补偿实现低温流体微重力方面尚未开展相关研究。本文将利用磁场、流体速度场等耦合的数值模拟方法,建立大范围、高水平的液氧微重力磁补偿环境,对不同磁场力均匀度条件下的气液两相界面在容器内的爬升过程进行模拟,并且与空间真实微重力环境(10-6g)进行对比,以确定液氧磁补偿微重力实验所依赖的超导磁体产生磁场力水平的技术要求,为后续的超导磁体微重力实验台的设计与搭建提供数据支持。
1 磁补偿微重力环境的实现
在磁场环境中,顺磁性物质液氧受到磁体积力的作用,因而如果液氧所受到的磁场力的方向与重力方向相反,理论上便能够得到等效的微重力环境。根据磁化理论,磁性流体在磁场中所受到的磁体积力fm为:

根据力平衡,则实现利用磁场力对重力g进行完全磁补偿的实现条件为:

式中:χ为磁化系数;μ0为真空磁导率;ρ为流体的密度。对于液氧,其磁化系数χ=3.45×10-3,密度ρ=1 141.8 kg/m3,则对应1 g所需的G0=8.15 T2/m。因而,若要得到均匀的磁场力环境,需要使得磁场强度B平方的梯度在一定范围内尽可能均匀。微重力的实现水平与该梯度均匀度密切相关,梯度越均匀,微重力水平越高。
通过超导磁体所实现的空间磁场力分布是不均匀的,均匀度越差意味着离理想的微重力环境相差越大。本文提出以下非均匀度指标对磁场力的非均匀度分布进行定量分析:

式中:εz为磁场力在Z轴方向上补偿的非均匀度,εz越低意味着磁场力在Z轴方向上与重力越接近,即越接近空间微重力环境。εr为磁场力在R轴方向上补偿的非均匀度。对给定的工质,对磁感应强度B进行二阶Tylor展开并利用麦克斯韦方程div(B→)=0和rot(B→B→)=0得到:
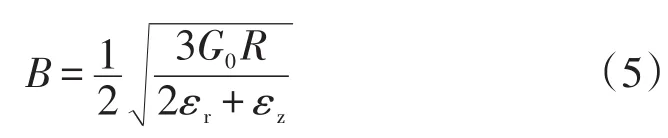
式中:B为磁感应强度;R为磁补偿区域的特征长度。对于给定的磁体结构和实验工质,不同的补偿范围对应着一组εz和εr的值。因此选取不同的补偿区域作为对象时,都可以计算出各自的εz,用于评估研究磁场力补偿的非均匀度对微重力实验的影响。
图1为比选后构建的某一个超导磁体线圈加载电流时在其内部及周边区域所形成的磁场分布及Z轴方向上磁场强度B和物理量G的分布曲线。超导线圈由两组线圈组成,外线圈内径250 mm、外径263.03 mm、高250.44 mm,内线圈内径266.72 mm、外径272.03 mm、高924.48 mm,内外线圈的工作电流均为135 A。所得到的磁场能够在Φ40 mm×60 mm的柱形区域内实现0.3%的磁场力不均匀度。由图1(b)可以看到,在Z轴坐标-0.263 m附近的区域内存在着一片与重力方向相反的均匀磁场力区域,该区域即为液氧的磁补偿理想区域。图2为超导磁体在Φ40 mm×60 mm区域内磁补偿的εz和εr的分布。由图2(a)能够看到εz沿补偿点呈中心对称分布。

图1 磁场分布及Z轴方向上磁感应强度B和物理量G的分布图Fig.1 Magnetic field distribution and distribution of magnetic induction intensity and physical quantity G in Z-direction

图2 Φ40 mm×60 mm磁补偿区域均匀性表征图Fig.2 Characterization of uniformity of Φ40 mm×60 mm magnetic compensation region
2 不同磁场力非均匀度环境下的自由液面爬升模拟
在上述模型和评价指标的基础上,选取不同大小的磁场力补偿区域,对区域内的液氧在0.1 MPa下的箱内自由液面爬升过程进行数值模拟,由此评估不同的磁场力非均匀度(0.05%、0.10%、0.30%、1.0%)工况与对应的空间真实微重力条件工况的特性差异。
2.1 网格划分及无关性验证
利用COMSOL Multiphysics软件对磁场、流场及多相流三种物理场在二维轴对称坐标下利用有限元方法进行了耦合计算。其中流场为层流,多相流采用水平集(Level Set)方法进行计算,物理场离散方法为有限元方法,模型中心轴线为轴对称边界条件,其余三个边界均设为壁面边界条件,且液体与壁面之间的接触角为15°。计算容差10-5,计算时间步长为计算残差控制的变时间步长。表面张力用CSF模型[13]:

式中:σ为表面张力系数,取13.2 mN/m;δ为界面delta函数;κ为界面曲率;n为界面单位向量。
模拟模型网格划分如图3所示,其中(a)为流场区域网格的放大,流场区域和磁体结构由四边形网格划分,其他区域由三角形网格划分。由于不同大小的流场区域需要不同的网格数量,因此分别对Φ17 mm×25.5 mm、Φ24 mm×36 mm、Φ40 mm×60 mm、Φ70 mm×105 mm的流场区域进行了网格无关性验证。为了能定量比较不同计算条件下得到的气液相界面,引入RMS均方根计算不同计算条件下气液相界面曲线之间的平均距离:

对Φ17 mm×25.5 mm的区域分别按0.000 75 m、0.000 5 m、0.000 375 m、0.000 25 m和0.000 1 m的网格单元进行划分;对Φ24 mm×36 mm和Φ40 mm×60 mm的区域分别按0.001 m、0.000 75 m、0.000 5 m、0.000 4 m和0.000 3 m的网格单元进行网格划分;对Φ70 mm ×105 mm的区域按0.003 m、0.002 m、0.001 m、0.000 75 m和0.000 5 m的网格单元进行网格划分,并将计算结果分别与最密的网格划分计算的结果进行对比,如图4所示。(a)为对Φ17 mm×25.5 mm的不同网格单元大小的计算结果与0.000 1 m网格单元的计算结果之间的均方根;(b)为Φ24 mm×36 mm的不同网格单元大小的计算结果与0.000 3 m网格单元的计算结果之间的均方根;(c)为Φ40 mm×60 mm的不同网格单元大小的计算结果与0.000 3 m网格单元的计算结果之间的均方根;(d)为Φ70 mm×105 mm不同网格单元大小的计算结果与0.000 5 m网格单元计算结果之间的均方根。结果表明,分别选取0.000 25 m、0.000 5 m、0.000 5 m、0.001 m的网格单元对Φ17 mm×25.5 mm、Φ24 mm×36 mm、Φ40 mm×60 mm、Φ70mm×105mm的计算区域进行划分比较合理。

图3 数值模拟模型网格划分图Fig.3 Mesh generation of unmerical simulation model

图4 不同计算模型的网格无关性检验图Fig.4 Grid independence test of different computing models
2.2 计算结果
图5 、图6、图7和图8分别为补偿区域Φ17 mm×25.5 mm、Φ24 mm×36 mm、Φ40 mm×60 mm、Φ70 mm×105 mm(对应的磁场力非均匀度分别为0.05%、0.10%、0.30%、1.0%)条件下,磁场力补偿(a)和空间零重力环境(b)液氧气液相界面的瞬态变化。
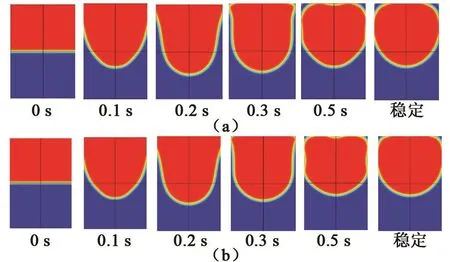
图5 0.05%非均匀度条件时磁补偿和真实微重力环境下氧气液相界面演化图Fig.5 Evolution of oxygen liquid interface under magnetic compensation and real microgravity at 0.05%inhomogeneity

图6 0.10%非均匀度条件时磁补偿和真实微重力环境下氧气液相界面演化图Fig.6 Evolution of oxygen liquid interface under magnetic compensation and real microgravity at 0.10%inhomogeneity
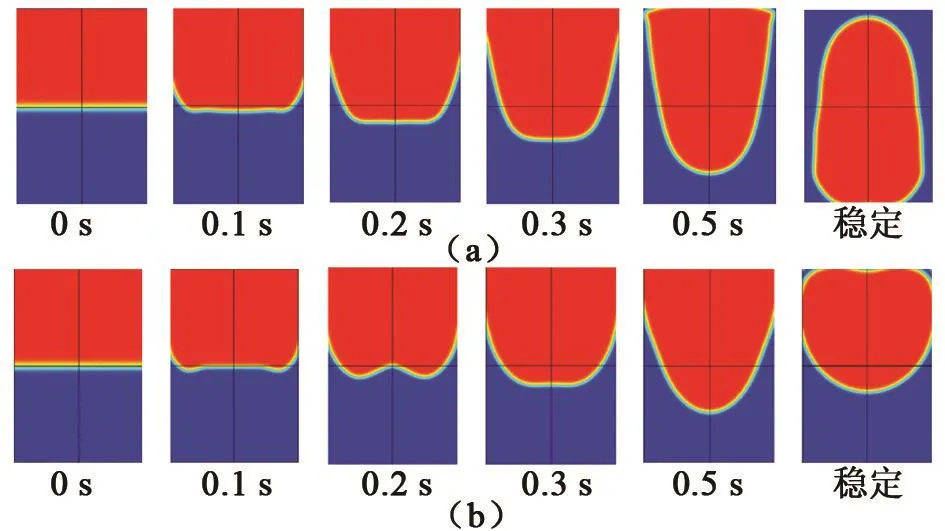
图7 0.30%非均匀度条件时磁补偿和真实微重力环境下氧气液相界面演化图Fig.7 Evolution of oxygen liquid interface under magnetic compensation and real microgravity at 0.30%inhomogeneity
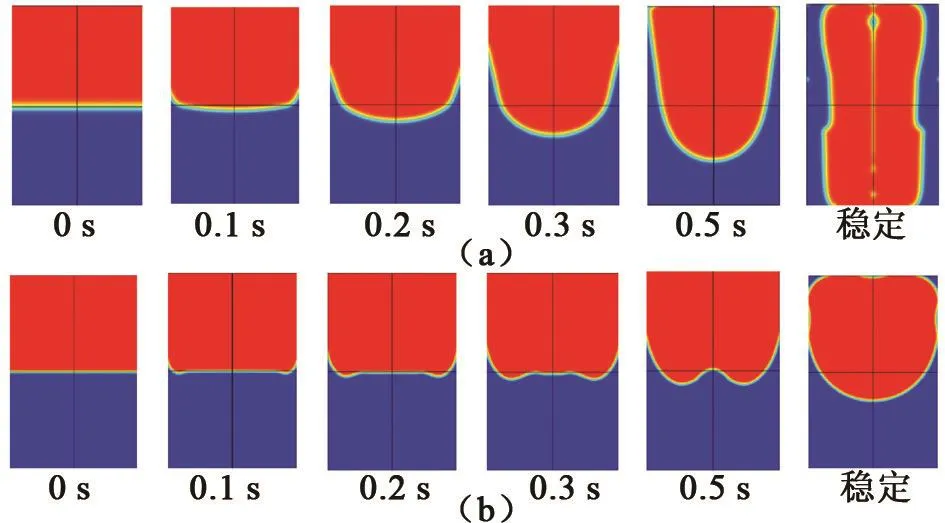
图8 1.0%非均匀度条件时磁补偿和真实微重力环境下氧气液相界面演化图Fig.8 Evolution of oxygen liquid interface under magnetic compensation and real microgravity at 1.0%inhomogeneity
2.3 结果分析
基于图5~8中的计算结果,将四种计算条件下的液面沿固体壁面的爬升过程以及磁补偿条件与对应的空间微重力条件下的气液相界面曲线平均距离进行了对比,如图9所示。

图9 四种区域范围内液体沿壁面的爬升过程及磁补偿条件与真实微重力条件偏离情况图Fig.9 The climbing process of liquid along the wall in four regions and the deviation of magnetic compensation condition from the real microgravity condition
RMS越小意味着磁补偿条件下的液面曲线与空间微重力条件下的液面曲线越相似,即更准确的补偿效果。由图9可见,在0.05%的非均匀度条件下,液氧在磁补偿环境下的自由界面流动能够很好吻合空间微重力条件(10-6g)下真实自由界面流动,特别是液面爬升阶段和形成稳定氧气枕阶段的时间标签都取得了较好的同步对应。
0.10%的非均匀度条件下,液氧在磁补偿环境下的自由界面流动无论是液面爬升阶段还是形成氧气枕阶段都得到了一定程度的还原,因此0.1%的非均匀度可视为能基本满足要求的磁补偿环境条件,优于此技术指标的工况将取得更佳的微重力模拟水平。
0.30%的非均匀度条件下,液氧在磁补偿环境下的自由界面流动能够部分还原空间微重力条件(10-6g)下的自由界面流动情况。在液面爬升阶段,磁补偿环境较好地还原了液氧液面沿固体壁面的爬升,但未能完全还原液氧底部随着爬升过程而出现的振荡现象。在形成稳定氧气枕阶段,磁补偿环境没能正确还原空间微重力环境下的液氧气泡。可见,虽然不均匀度仅仅从0.10%恶化到0.30%,所带来的微重力模拟水平却出现了明显下滑。
1.0%以内的非均匀度条件下,液氧在磁补偿环境下的箱内自由界面流动基本上不再能够还原空间微重力条件(10-6g)下的自由界面流动。无论是在液面爬升阶段还是形成稳定氧气枕阶段,液氧液面均与空间微重力环境下的真实爬升速度、形状出现了明显的差异。由于非均匀磁场力的干扰,氧气泡会在液体内不断地变形运动而无法形成稳定的氧气枕。
2.4 规律拓展分析
为了研究更一般性的规律,通过改变磁补偿区域的大小,对0.05%~1.0%共11个工况的不同非均匀度磁场力下的气液相界面变化过程进行了模拟。图10为曲线平均距离RMS在5 s计算时间内的平均值随磁场力非均匀度的变化情况,反映了真实微重力环境与磁补偿微重力环境下计算得到的液面曲线间的差异随磁场力非均匀度的变化情况。空间微重力环境下与磁补偿环境下气液相界面之间的相似程度仅在0.10%以内的补偿情况下有了明显的降低,说明在0.10%以内的磁场力非均匀度条件下,液体沿壁面的爬升过程以及包裹气体形成气泡的过程开始得到较好的还原,而在更低的非均匀度条件下(0.05%)则能够得到很高的真实微重力状态还原度。

图10 平均RMS随磁场力非均匀度的变化Fig.10 Variation of mean RMS with inhomogeneity of magnetic field force
3 结论
本文对顺磁性流体液氧在磁场力作用下实现微重力悬浮的自由界面流动过程进行了磁场、流场、多相流耦合的数值模拟,研究了磁场力的非均匀度对液氧磁补偿微重力自由界面的影响。提出了评估磁场力非均匀性的定量指标和评估方法,通过与空间真实均匀微重力环境的比对,发现磁补偿微重力环境的制造水平对磁场力的非均匀度很敏感。在0.05%的非均匀度磁补偿条件下,不管是液氧液面爬升过程还是形成气枕的过程,均可实现很高的真实微重力状态还原度;在0.1%的非均匀度磁补偿条件下,磁补偿微重力环境初步具备还原空间微重力环境的能力;非均匀度恶化到0.3%时,仅能对液氧的液面爬升过程进行可接受的模拟,其液体底部的振荡过程和氧气枕形成过程都出现明显的偏差;当进一步恶化到1.0%的非均匀度时,所有过程均出现了明显差异,甚至气液相界面会无法稳定,基本判定已不适合用于空间微重力真实状态模拟。上述研究结论有助于确定液氧磁补偿微重力实验所依赖的超导磁体产生磁场力水平的技术要求,为后续的超导磁体微重力实验台的设计与搭建提供数据支持。

