水下传感器网络节点部署算法*
朱飞,王忠思,姚琦
(海军士官学校 信息通信系,安徽 蚌埠 233012)
0 引言
水下无线传感器网络(underwater wireless sensor networks,UWSN)在海洋环境监测、灾害预防、资源勘探等民用领域和水下战术监视、入侵监测、武器侦察定位等军事领域有着广阔的应用前景,已经得到世界各国研究机构的极大关注[1]。我国拥有1.8万km大陆海岸线、1.4万km岛屿海岸线和300万km2的管辖海域面积,海洋渔业资源、矿业资源丰富,是我国国民经济发展的重要源泉[2]。近海3条海上交通线,是我国海上军事、经济运输的大动脉,是海军沟通各主要基地,实施战役编队机动的战役通道[3]。因此,构建我国重要海区通道的三维监视网络进行海洋监测侦察、信息搜集,对于确保我国海洋权益、经济利益、国防安全具有十分重要的战略意义。
1 国内外研究现状
最早开展UWSN研究的国家是美国,早在20世纪50年代,美国就在大西洋和太平洋中投入大量经费建设了一个庞大的水声监测系统(sound surveillance system,SOSUS),以实施海洋监测[4]和海洋战术监视。作为美国比较成功的水下网络之一的美国海军海网(Seaweb)水下声学网络是目前应用较早的具有典型代表意义的水下传感器网络项目,美国海军主要将其用于沿海区域的警戒,这种可布放的自主分布系统能够实现命令、控制、通信和导航功能,在反潜战和反水雷领域具有良好的应用效果。此外,日本的地球区域实时监测计划ARENA、欧洲的海洋气象监测网络ESONET、蒙特利海湾研究所MBARI建立的海洋生化监测系统LOBO和海洋监测系统MOOS、北太平洋中铺设的有缆绳海洋监测系统NEPTUNE工程和设在纽约西长岛南部的前沿分析观测网络和遥测系统FRONT等[5-7],目标都是通过UWSN实现海洋多学科、多要素的综合研究,这些项目的研究和应用为我们提供了重要的参考和借鉴意义。
随着UWSN研究的兴起,许多厂商开始研制并生产水下节点,如澳大利亚DSPComm公司的AquaNetwork系列产品,美国的Teledyne Benthos水声通信设备,英国的微型水下声学调制解调器等。目前,Tritech微型水下声学调制解调器通信距离可以达到500 m,数据传输速率为40 bit/s。图1给出了海底联合战术监视网络的拓扑图,由水下传感器节点、水下通信调制解调器、无线通信数据链、舰船、飞机和卫星构成一个完整的三维立体网络,实现对水下入侵目标的监测,特别是对于安静型潜艇的探测具有重要的战术价值。

图1 海底联合战术监视网络拓扑图Fig.1 Network topology of undersea joint tactical surveillance
国内相关研究机构和高校也已开始着手对水下通信进行研究。近年来,经过众多研究人员的不懈努力,出现了一批重要的研究成果[8]。
在UWSN的许多应用中,除使用自带动力系统的机动节点,如水下机器人、自主航行器(autonomous underwater vehicle,AUV)和水下滑翔机(underwater glider,UG)之外,一般均采用水下固定锚节点,进而实现诸如重要战略通道监视(栅栏覆盖)、重要海区监视(面覆盖)和水下监视定位(三维覆盖)等功能。固定节点的部署方式主要有受控部署和随机部署2种[9]。在受控部署中,通过计算得出满足某些条件的特定位置,再将传感器节点部署于这些特定位置上,这种部署需要进行人工干预以使得节点准确的进入特定位置,其部署效率往往较低。随机部署一般是使用飞机、舰艇或潜艇将大量节点抛洒在监测水域,尔后这些节点通过锚固定在海底或者通过缆绳连接在水面浮标,从而扩展到水下不同深度实现三维覆盖。本文研究水下固定节点随机部署策略的最优化部署方案。
2 网络模型与最优部署
2.1 网络模型
节点一旦被部署后不能水平移动,只能在垂直方向上任意沉降,监测区域为某海域水下一个长方体区域F(L×W×H)。节点感知模型为布尔模型,节点感知半径为Rs,通信半径为Rc。在初始阶段,有M个节点被随机部署于监测区域二维水面,随后,这些节点会被锚固定在海底,节点所处深度由连接锚与节点间的缆绳长度所决定。节点在随机布放后能通过自身的定位系统获知自身坐标,并传送给中心节点。
2.2 三维覆盖最优部署模型
在二维平面中传感器节点的覆盖模型是以圆形表示的,而将其拓展到三维空间则是以球形表示,这种覆盖模型与三维空间内的球堆积问题相一致。球堆积问题[9](sphere packing problem,SPP)是指在已知的空间中找到球最密集的放置方式,一些常见的球堆积结构如简单立方格、体心立方格和面心立方格已经被广泛研究和应用,图2给出了空间对称格结构的泰森图划分[10]。可以看出,简单立方格结构对于空间的三维泰森图划分是立方体,而体心立方格结构和面心立方格结构对于空间的三维泰森图划分则分别是截顶八面体和菱形十二面体。
2.3 最小节点数计算
按照以上空间划分法,令L,W,H分别为覆盖区域在x,y,z轴方向上的长度;Δx,Δy,Δz分别为节点在x,y,z轴方向上的间距;[m]表示不小于m的最小整数;Rc为节点通信半径。则完全覆盖三维区域F(L×W×H)的最小节点数N可由式(1)计算,式(2)中Nt为体心立方格结构部署方案最少节点数,式(3)中Nm为面心立方格结构部署方案最少节点数。
(1)
(2)
(3)
3 基于图案模型的节点沉降部署算法
3.1 总体方案
本文提出基于理想图案模型的节点沉降部署方法,分为3步:第1步初始化阶段,主要是完成节点的随机部署和初始拓扑构造,根据节点感知半径和通信半径计算最小节点数以及理想图案位置坐标(图案计算DPC),然后将水面随机部署节点与理想图案位置一对一的进行匹配(图案节点选择PNS),并保证沉降节点与理想图案位置的水平距离偏差总和最小。第2步连通度修复阶段,本文提出“插入调整法(NCR-IA)”、“调整法(NCR-A)”2种算法,以保证匹配节点沉降到水下区域后仍然能构成一个连通的网络。第3步覆盖空洞修复阶段,本文提出的覆盖空洞修复算法CHR[11],在连通度保证的同时,使得网络覆盖率最大化。图3给出了基于图案模型的节点沉降部署算法流程。

图2 空间对称格结构的Voronoi划分Fig.2 Voronoi tessellation Via cubic lattice structures
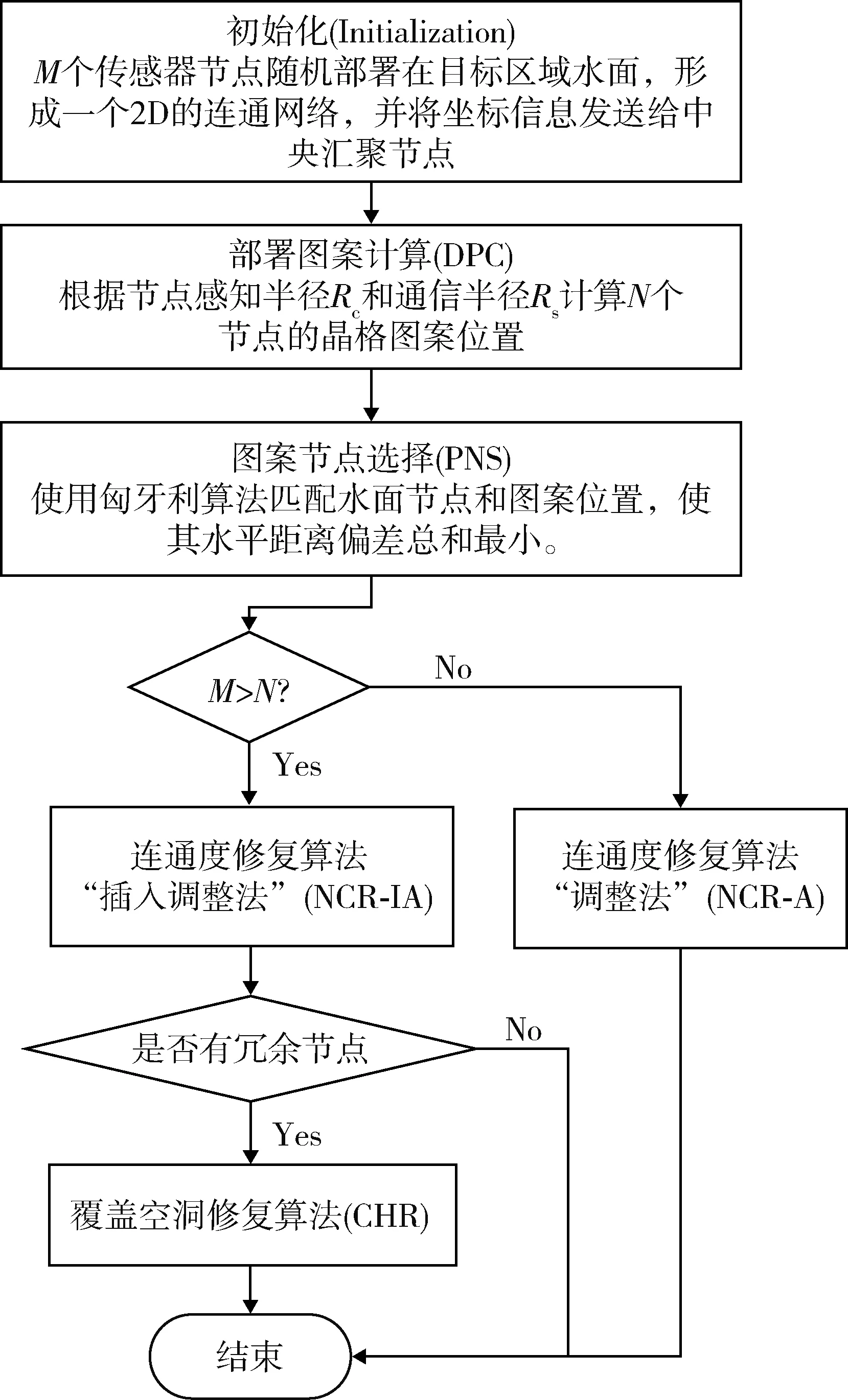
图3 基于图案模型的节点沉降部署算法流程Fig.3 Flowchart of Nodes sinking algorithm via pattern model
3.2图案节点选择PNS
图案节点选择采用加权二分图完美匹配方法,将水面大量随机部署节点(子集A)基于距离权值一对一的分配给区域内的理想图案位置(子集B),实现“N项目”与“N目标”的最佳匹配。对该目标分配问题进行建模,现设子集A中随机节点个数为M,子集B中图案位置(最少节点数)为N,则目标分配问题的模型可以描述为
(4)
满足以下条件:
xij={0,1},
(5)
(6)
(7)
式中:D=(dij)M×N为距离评价矩阵,dij为第j个随机节点距离第i个理想部署点的水平欧式距离。
因为锚节点在垂直方向的高度可以根据需要任意调节,因此节点沉降后其垂直方向上的距离差Δz=0,在距离评价矩阵中只考虑随机部署节点与理想部署位置的水平欧式距离。令X=(xij)M×N为节点目标分配的解矩阵,当xij值为1时,表示随机部署节点i指派给理想部署位置j,否则,未指派。条件(6)限定解矩阵的每一行只能有一个1,即一个随机部署节点只指派一个理想图案位置,条件(7)限定解矩阵的每一列只能有一个1,即一个理想图案位置只分配一个随机节点。
3.3 连通度修复算法NCR-A和NCR-IA
待上述匹配节点沉降至水下后,为检查和修复网络连通度,首先需要找出N个沉降节点哪些构成连通的网络,哪些相互之间不连通。采用图论中适用于遍历和搜索树或图数据结构的广度优先算法[12](breadth-first search,BFS)找出匹配节点中不连通的网络分区,即子网S1,S2,…,Sn,然后对其进行连通度修复。图4给出本文网络连通度修复算法

图4 网络连通度修复算法图例Fig.4 Network connectivity the restoration
的一个图例。
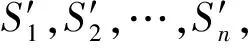
3.4 覆盖空洞修复算法CHR
一般来说,随机节点个数M大于完全覆盖所需最少节点数N,即存在冗余节点。为提高网络覆盖率,考虑利用冗余节点进行覆盖空洞修复。对于覆盖空洞的检测和修复,本文提出基于三维泰森图(3D-Voronoi)晶胞结构的覆盖空洞检测方法和基于K-means聚类算法的覆盖空洞修复方法。
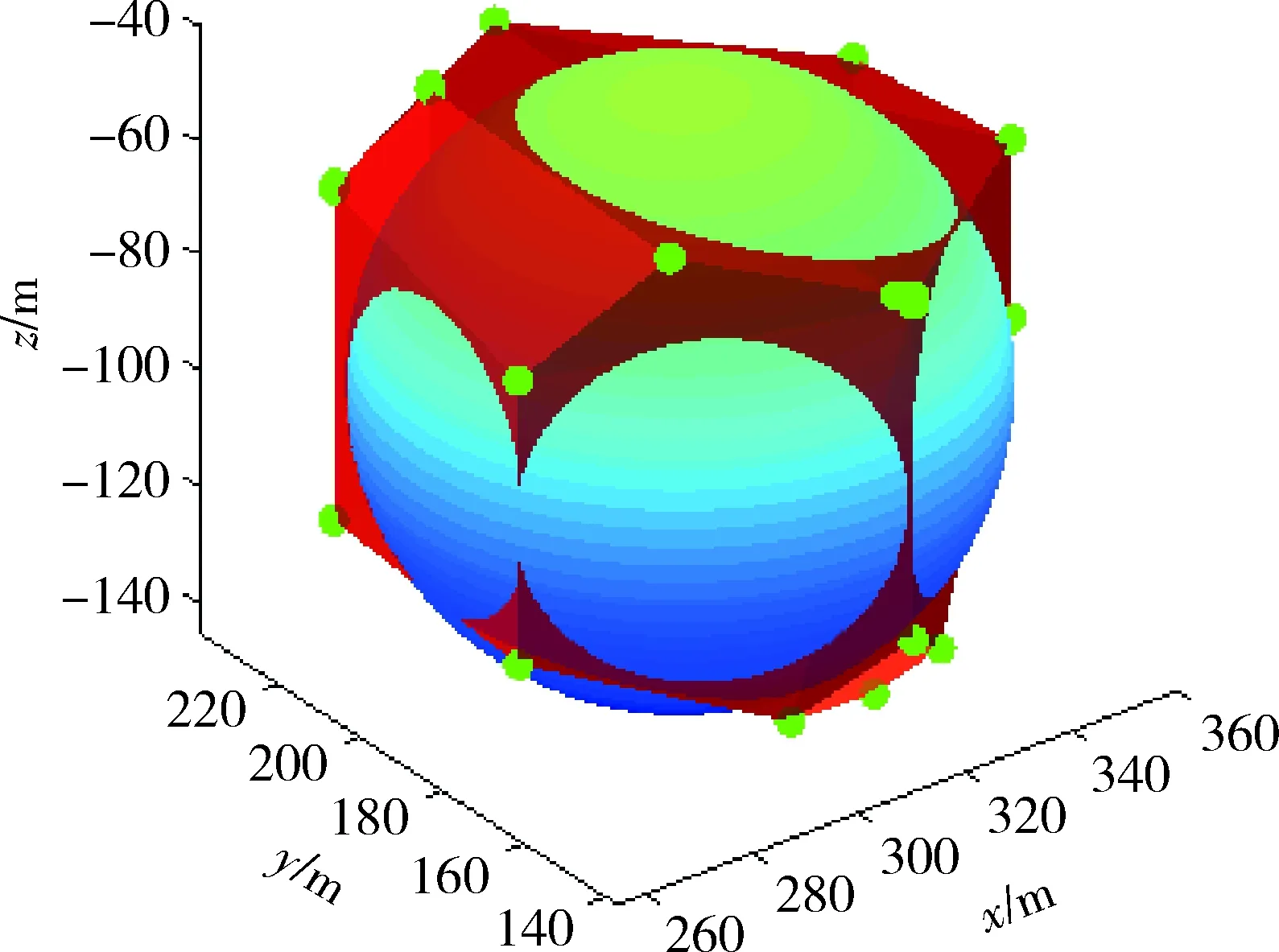
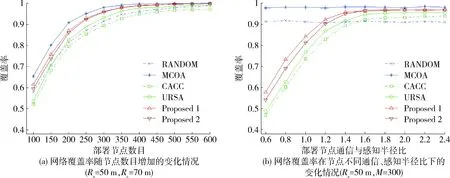
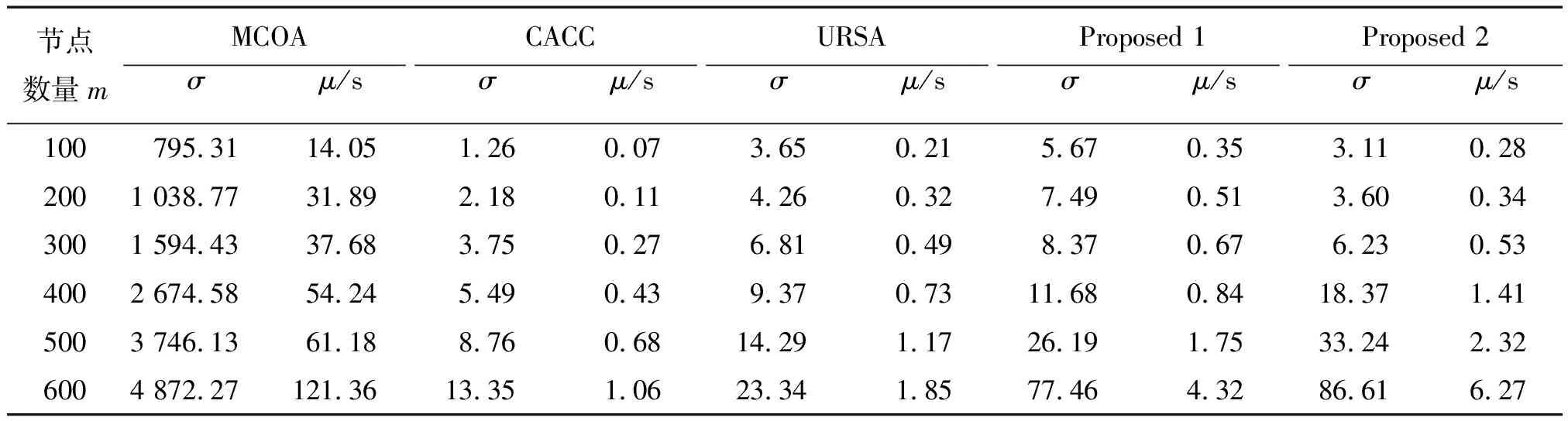
首先,三维泰森图的定义如下:设P={p1,p2,…,pn}⊂R3是三维空间的n个点,d={p,pi}为空间任一点p和pi之间的欧式距离,将由V(pi)=∩j≠i{p∈R3|d(p,pi) 要实现对覆盖空洞的修复,需要将冗余节点沉降到覆盖空洞的位置。设节点指派后的冗余节点个数为M-N,令其等于K,则空洞点集H的聚类个数为K,聚类簇的质心位置为冗余节点的沉降位置。由于空洞点集的密集程度与该区域空洞点的大小之间存在一定的相关性,即一般来说空洞点密集的地方覆盖空洞也较大。鉴于以上特征,冗余节点可以指派到覆盖空洞点集的簇心位置,由于部署节点只能在初始部署位置的垂直方向沉降,因此K个聚类簇的簇心只能是簇成员的z轴质心。使用K-means聚类算法得到K个沉降坐标的步骤如下: 图5 部署节点的三维泰森图与覆盖效果图Fig.5 3D-Voronoi of deployment nodes and the coverage effect 图6 节点覆盖球、泰森晶胞和覆盖空洞点示意图Fig.6 An illustration of coverage sphere, voronoi cell, uncovered vertexes 第1步:随机赋予K个剩余节点一个z坐标,联合其水平坐标,作为K个初始簇心; 第2步:对所有的空洞点计算其到每个簇心的距离,并聚类到距离最近的簇心; 第3步:计算K个簇的z轴质心; 第4步:迭代2~3步直至每个簇中点集成员不再发生变化,算法结束。 得到的K个簇的簇心位置即为冗余节点的沉降位置,冗余节点沉降后能够尽量多地覆盖空洞点,从而实现覆盖空洞的修复。 图7比较了几种算法的网络覆盖率。从图7a)可以看出,网络覆盖率随节点数目增加而增大,但趋势会逐步放缓。RANDOM方法保证了节点在目标区域的均匀分布,因此,其性能稍微优于CACC算法,而与URSA算法相当。需要注意的是,MCOA算法作为一种通过全局搜索节点最佳沉降位置的穷举算法,在网络覆盖率性能上始终保持最优,但是该算法的时间复杂度很大。从图7b)可以看出,在部署节点数目不变的情况下,网络覆盖率随节点通信半径增加而增大,但趋势会逐步放缓,而RANDOM方法和MCOA算法保持不变,这是因为该2种方法的部署不保证网络连通度,而本文提出的算法和CACC算法、URSA算法均需要保证网络的全连通,当节点通信半径增加时,这些算法会增加节点距离以减少节点间的覆盖重叠区域,因此,网络覆盖率会随节点通信半径增大而增加。综合两图来看,在保证网络连通度的前提下,本文提出的算法与CACC算法和URSA算法相比,网络覆盖率性能提高平均达8%~9%和3%~4%。 图8比较了几种算法的网络连通度。从图中可以看出,对于RANDOM和MCOA算法,无论是增加部署节点数量还是增大节点通信半径,都对网络连通度的提高有帮助。而本文提出的算法和CACC算法、URSA算法均能保证网络的全连通,连通度达到100%。 表1给出了几种算法的时间复杂度,μ表示算法的执行周期均值,σ表示方差,节点通信半径Rc=70 m。MCOA算法作为一种穷举算法,在每次迭代中均需要重复计算网络覆盖率,因此耗费了大量时间。本文提出的算法时间复杂度稍微大于CACC和URSA算法,这是因为在连通度修复阶段,可能需要进行一些迭代找出修复节点所处的最佳深度。但总体来看,本文算法和CACC算法、URSA算法,时间复杂度均处于同一数量级,明显低于MCOA算法。 图7 几种算法的网络覆盖率比较Fig.7 Network coverage ratio comparison 图8 几种算法的网络连通度比较Fig.8 Network connectivity comparison 表1 仿真实验中的参数设置Table 1 Comparison of the complexity of different algorithms 本文研究了连通度保证下的水下传感器网络三维覆盖优化问题。针对水下固定锚节点一经部署,水平坐标无法改变的问题,提出了基于图案模型的节点选择与沉降三步解决方案。仿真结果表明,提出的算法在保证网络连通度的情况下,具有更好的网络覆盖率性能,与集中式算法相比,能有效降低算法的时间复杂度。该方法研究的初衷虽然是解决水下监视网络三维覆盖问题,分析可知,其可推广到矿山、森林、国土边界、太空等任何一个三维空间实施有效的监视覆盖,进而实现侦察定位、预警探测、灾害预防等军民应用领域。
4 仿真评估
4.1 仿真环境与参数设置
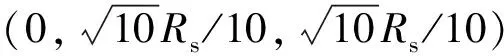
4.2 仿真结果与分析

5 结束语

