基于随机频率捷变的窄带雷达成像方法*

周志增,刘洪亮,刘朋,王永海

(中国洛阳电子装备试验中心，河南 孟州 454750)

0 引言

雷达成像技术应用最多的是合成孔径雷达(synthetic aperture radar，SAR)。SAR在径向距离上依靠宽带信号实现高分辨，几百MHz的频带可将距离分辨率缩小到亚米级。逆合成孔径雷达(inverse synthetic aperture radar，ISAR)在发射信号过程中，可视为等效反向运动而形成阵列，据此也可提高距离分辨率。而窄带雷达信号的带宽一般不超过10 MHz，距离分辨率不高，其分辨单元通常大于目标，只能视目标为点目标。如果参照成像雷达的信号处理方法，将窄带雷达的某些信号进行合成使之具有宽带信号特征，就可以提高窄带雷达的距离分辨率，进而可能成二维像[1]。

大多数现代窄带雷达具有频率捷变信号，这种信号常用来抗电子干扰，因为其可在极短时间内覆盖较宽载频范围，有一定概率跳开干扰范围。正是基于频率捷变信号“短时覆盖较宽载频范围”的特点，若能采用以时间换带宽的方法，将频率捷变信号等效为大带宽的线性调频信号，在回波处理过程中进行积累处理，并进行速度补偿，便可以在径向距离上成出一维距离像，进一步可能实现二维像。本文以窄带雷达随机频率捷变信号为对象，研究了随机频率捷变信号成像的方法。

1 频率捷变信号成像原理

1.1 一维像合成

为推导简便，假设雷达发射信号为规则递进的频率捷变信号(类似步进频信号)，脉冲重复间隔为T，脉宽为τ，载频为f0，步进频率间隔为Δf，脉内是线性调制。频率捷变信号第i个脉冲的中心频率为[2]

fi=f0+iΔf,i=0,1,…,n-1.

(1)

在一个脉冲串内，第i个频率捷变的发射波形可以描述为

(2)

式中：θi为相对相位；Ci为常数。

在距离R0处的目标在时间t=0时的接收信号为

sri(t)=Cicos[2πfi(t-τ(t))+θi]，
iT+τ(t)≤t≤iT+τ+τ(t).

(3)

其中，往返时延τ(t)为

(4)

式中：c为光速；v为目标的径向速度。

为了提取正交分量，接收信号Sri(t)下变频到基带。即和下面信号混频

yi(t)=Cicos(2πfit+θi)，iT≤t≤iT+τ.

(5)

经过低通滤波器后，正交分量为

(6)

式中：Ai为常数，并且

(7)

这就是每一脉冲从发射到接收的相位超前项。

混频器输出正交分量的采样时刻在t=ti被采样，该时刻是按等时间间隔T增长，以便在每一脉冲中心进行取样,τr是与对应于距离像起点的距离有关的时延。

(8)

正交分量的复数形式可以表示为

Xi=Aiejψi.

(9)

式(9)表示基于单个脉冲串的目标反射性的频域样本，该信息可以利用IDFT(inverse discrete fourier transformation)转化为一系列距离延时的反射性(即为距离像)大小，表示为

(10)

进行合并得到

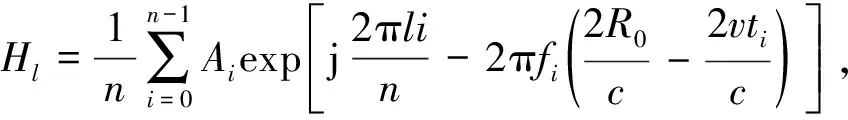
(11)

对n归一化，假设Ai=1，目标为静止的(v=0)，则式(11)可以写为

(12)

利用fi=iΔf得到

(13)

简化为

(14)

式中：

(15)

最后，合成的距离像为

(16)

这是由点目标产生的综合距离剖面的包络。

1.2 二维像合成

假设用于成像的频率捷变信号波形包含M个脉冲串，每个脉冲串包含N个窄带脉冲，同一个脉冲串内N个脉冲的载频线性步进。在第m个脉冲串内第n个脉冲时刻mTD+nTr(TD为驻留时间)发射载频为fn，调频斜率为γ，脉冲宽度为Tp的线性调频信号[3]：

exp[j2πfn(t-nTr-mTD)],

(17)

式中:fn=f0+nΔf；m=0,1,…,M-1；n=0,1,…,N-1；且-Tp/2≤t≤Tp/2。

目标反射回波的频率响应可表示为

(18)

式中：f为载频；r为目标的瞬时径向距离；A为与发射功率、天线增益、传输损耗、处理增益和雷达系统损耗有关的幅度；H(p,q)为目标回波的传递函数。

定义目标回波的传递函数H(p,q)为

H(p,q)=∬h(x,y)exp[j2π(px+qy)]dxdy，

(19)

式中：p=2(f/c)sinθ，q=2(f/c)cosθ；θ为雷达坐标系和目标坐标系的夹角。

对于规则递进的捷变频雷达信号，f在fn中取值，r=r0+rm,n，θ=θm,n，相应地，p=2(fn/c)sinθm,n，q=2(fn/c)cosθm,n。

此时，频率响应为

(20)

式中：H(m,n)为目标对电磁波的反射特性：

H(m,n)=∬h(x,y)exp[j2π(pm,nx+qm,ny)]dxdy.

(21)

进一步处理可得：

(22)

此时散射点在径向距离上分开。

对h(k,n)中每个距离单元包含的M个复数作DFT(discrete fourier transformation)：

(23)

就可以把横向距离上的散射点分开，得到二维像D(m,n)。

2 随机频率捷变信号成像理论分析

随机频率捷变分为2种情况：

(1) 捷变频点具有较好的完备性，能包括捷变间隔内的所有频点且每个频点具有唯一性；

(2) 捷变频点完备性较差，不保证捷变间隔内每个频点都能发射出去，且同一个频点不具有唯一性。

对于第1种情况，情况较为简单，预处理方法为：对频点进行排序后，把随机的频点所对应的回波进行重排后，就可以进行下一步处理。重排后频点无丢失，合成带宽完整，捷变间隔不变。

对于第2种情况，情况较为复杂，预处理方法同第1种，带来的问题就是合成带宽内有缺失，且缺失多少无法预知，给一维像合成带来的影响较大，一是频点丢失和频点重复导致合成带宽变小，同时捷变间隔不固定。合成后的一维像受栅瓣影响较严重，且分辨率下降。可通过调整子脉冲的时宽、进行加权失配滤波以及采用对子带进行加窗等方法对栅瓣进行有效抑制[4-6]。

随机频率捷变与规则频率捷变信号的不同，体现了多普勒性能的差异。假设目标以速度v相对雷达运动，则第i个脉冲的复采样信号相位为

(24)

式中:τr为雷达接收机的转移时延，为定值；s(i)为频率跳变的随机数列，覆盖所有频点。

按照发射频率递增的顺序重排后的相位关系为

(25)

其中：r(k)为s(i)重排后产生的随机数列。可以看出，式中第1项是与距离有关的线性相位项，是产生合成距离像必须的；第3项是目标速度和回波延时乘积产生的线性相位项，值较小，可以忽略。而第2项是目标速度产生的随机相位项，大小和雷达信号重周长度和数量有关。因此，对于随机捷变信号，目标运动相当于在采样信号的相位中加入了随机噪声，结果是导致合成距离像的峰值降低和波形发散。

3 随机频率捷变信号成像处理方法

根据频率捷变ISAR成像原理[7]，处理方法分为提取回波数据、预处理、速度估计、运动补偿、距离像合成、包络对齐、相位补偿以及最后的二维成像等步骤过程，其处理流程如图1所示。

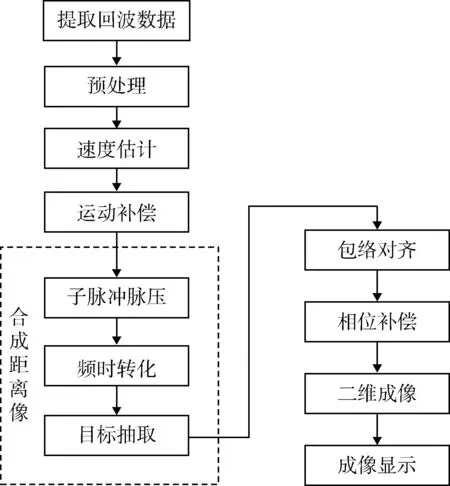
图1 频率捷变ISAR成像信号处理流程Fig.1 Signal processing of ISAR imaging with frequency agile

3.1 回波数据预处理

首先通过中频采集系统采集中频回波数据，采集的数据如图2所示。其中，X轴为采样单元数，Y轴为脉冲个数，Z轴为信号幅度值。随机频率捷变体制的主要问题在于回波对应的频点随机出现，需要根据雷达控制字进行重新排序。另外，存在距离-速度耦合和距离像发散。当目标具有加速度和速度时，频率捷变帧间高分辨距离像存在严重的距离走动，会造成高分辨距离像的移位和畸变，并使二维像散焦模糊，影响积累和横向成像质量。为此，必须进行运动补偿。

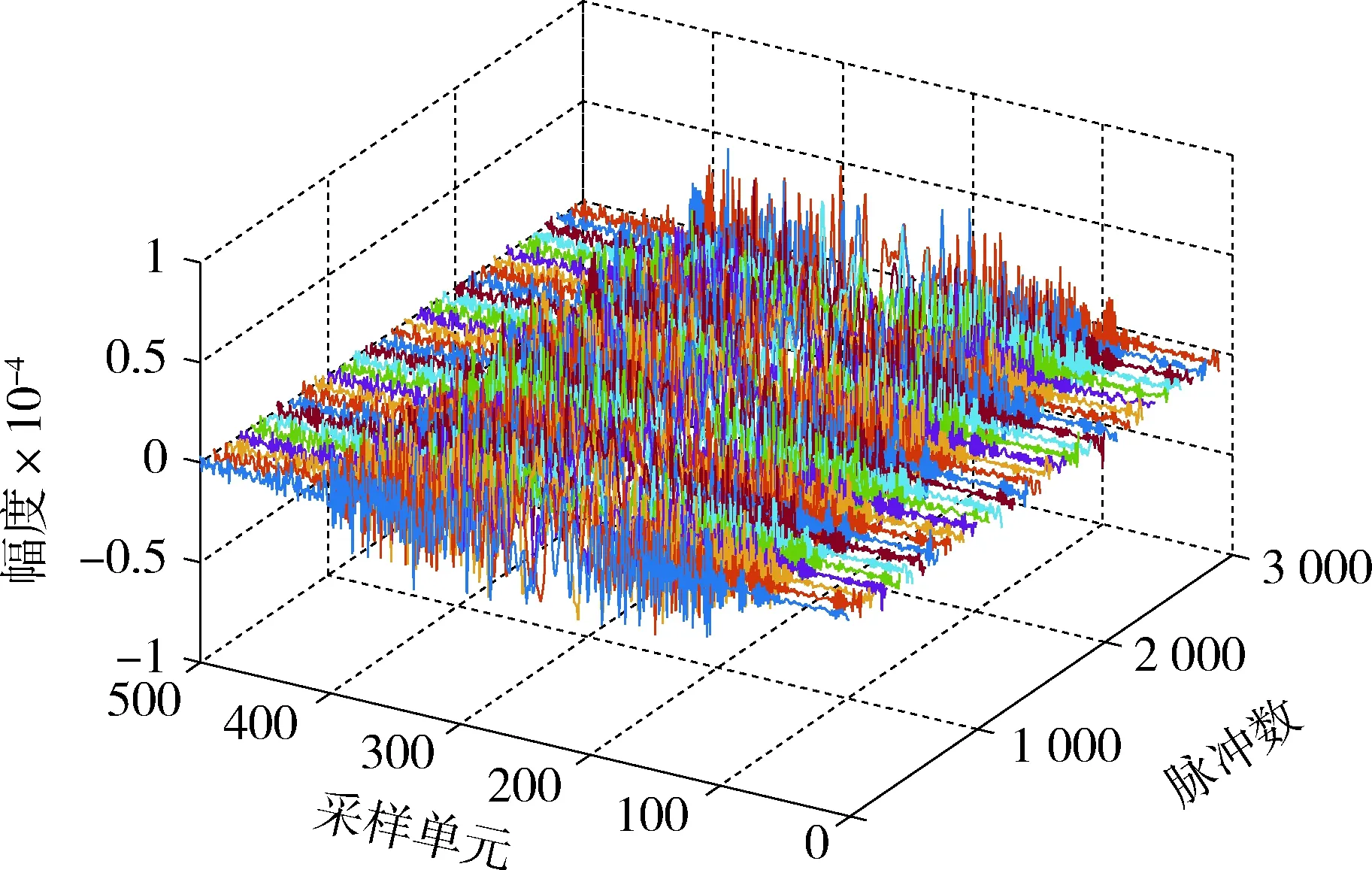
图2 中频采集回波数据Fig.2 Intermediate frequency acquisition of echo data

3.2 一维距离像的处理

通过对子脉冲进行压缩形成粗的距离像、频时转化、目标抽取等过程完成距离像的合成。其中，目标抽取能剔除冗余和分散的信息，对成像质量影响很大。目标抽取主要采用舍弃点迹提取法，基于每组IFFT(inverse fast fourier transform)结果所包含“距离新息”只存在于rs(rs为采样间隔对应的采样距离)的假设，直接从每组IFFT结果中取出长度为rs的信息拼接起来，舍弃其他点。这种方法实现简单，但由于只保留了IFFT有效区域的最开始部分，会造成信噪比的损失[8-10]。

3.3 二维像的处理

对于常规运动目标进行二维成像前往往需要运动补偿。根据补偿精度的不同，补偿过程一般分为距离对准和相位补偿2步，距离对齐将相邻回波信号在距离向对齐，并把目标距离走动造成的多普勒相位变化补偿掉。当前距离对准算法主要包括3类：第1类是最早提出来的散射重心法；第2类主要利用一维距离像之间的相关性进行对齐，称为相关对齐法；第3类是基于图像准则的对齐方法，主要包括最小熵法和最大峰度法。由于距离对准的精度要求不高，一般只要保证相邻一维像的最大对准误差小于半个距离单元即可，本文在处理时使用了第2种方法中的积累互相关距离对准算法，对于大多数成像场景来说，该算法能获得满意的对齐效果[11-12]。

理论上可以使用距离对准得到的距离偏移量的估计值进行相位补偿，但是要达到所需的相位补偿精度，距离估计精度应达到1/10雷达波长的量级。而实际的距离对准精度与波长相比差距很大，无法用距离偏移量的估计值实现相位补偿，因此必须采用其他方法对平动相位分量进行估计和补偿。基于散射点相位补偿方法的主要思想是从单个散射点，或多个散射点的综合，或等效的目标重心中获取平动相位信息。主要包括单特显点法、多特显点综合法、多普勒中心跟踪法等，这类方法运算量小、容易实现。本文在处理时采用单特显点法[13-15]。

4 随机捷变成像仿真分析

仿真实验主要针对静止目标和运动目标2种，分别合成一维像处理和二维像处理。

4.1 一维像处理

仿真验证条件：雷达工作在X波段，信号带宽为4 MHz，规则频率捷变间隔递进为4 MHz，子脉冲个数为64个，模拟目标由4个散射点组成，仿真分为静止和运动2种情况，即速度值分别为0 m/s和10 m/s。合成带宽为256 MHz，合成后距离分辨率为0.585 m。

图3为随机频点分布情况，图4为采用随机频率捷变信号处理得到的静止目标一维距离像。从结果中可以看出，频率捷变成像算法能完成模拟目标合成像的处理。

图3 随机频点分布Fig.3 Random frequency distribution

图4 静止模拟目标一维像Fig.4 One dimension of stationary analog target

图5a)为采用随机频率捷变信号处理得到的运动目标一维距离像，由于速度值的影响，距离像发生发散且出现杂乱现象，无法有效对目标进行识别。图5b)是进行速度补偿后的结果，补偿误差为0.4 m/s。可以看出，补偿后的一维像恢复正常，由于补偿存在误差，散射点强度有所损失。

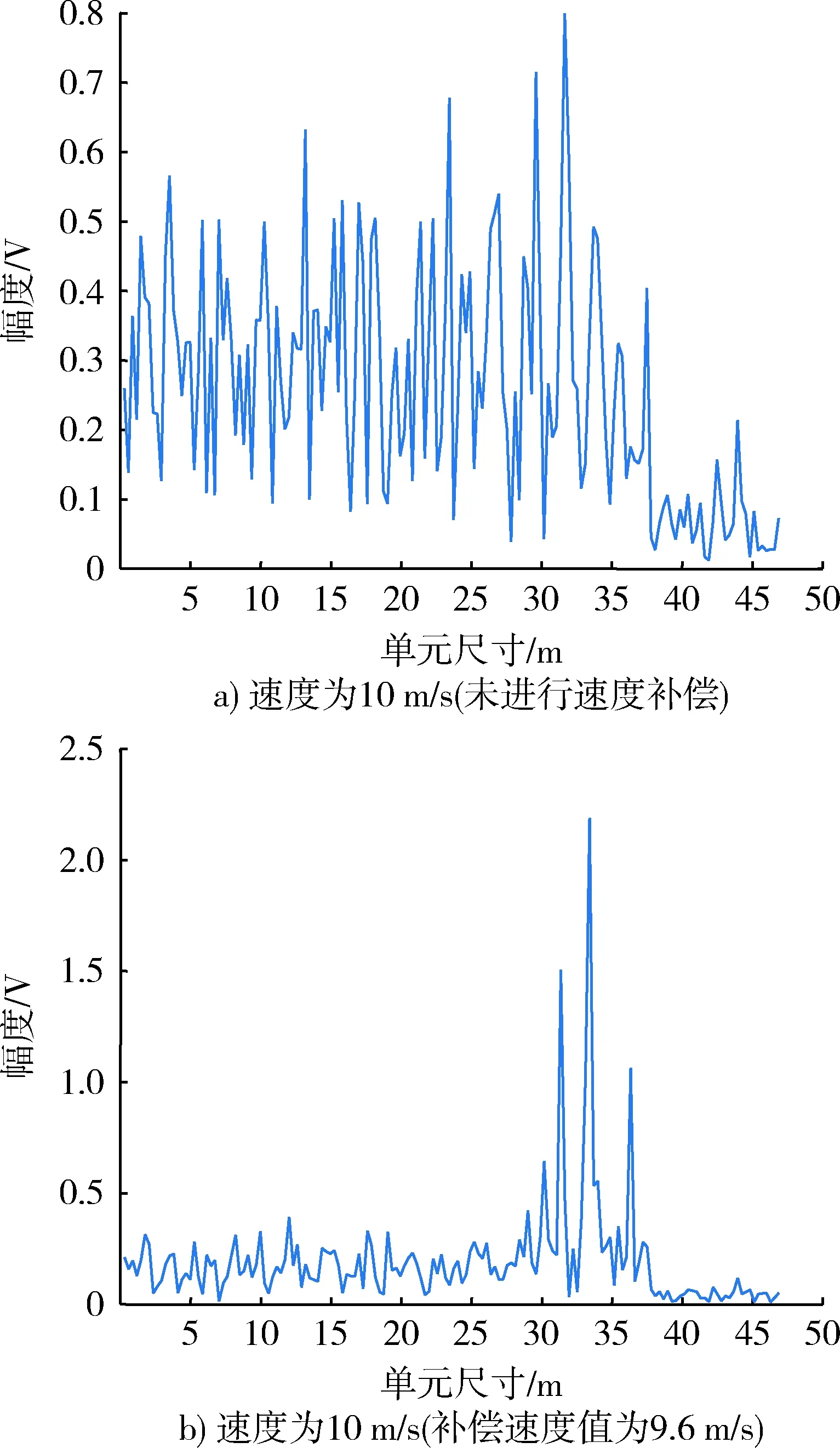
图5 运动目标一维距离像Fig.5 One Dimension of Movable Target

4.2 二维像处理

仿真验证条件：雷达工作在X波段，信号带宽为4 MHz，规则频率捷变间隔递进为4 MHz，脉冲串个数为128个，子脉冲个数为64个，模拟目标由10个散射点组成，转动角速度为0.003 rad/s，合成带宽为512 MHz，合成后距离分辨率为0.292 m。仿真目标模型如图6所示，共有11个散射点组成。

对图6目标进行成像，图7a)为未进行进行频点重排后的二维像，由于频率的随机性，导致二维像在距离维和多普勒维散焦严重，无法获取成像结果。图7b)为进行频点重排后的处理结果，结果和模型相一致。

5 试验验证

利用一部X波段窄带雷达跟踪标校球，采集随机频率捷变数据，验证随机频率捷变信号成像的可行性。雷达信号带宽为4 MHz，频点捷变点数为64个，捷变间隔为4 MHz，相当于合成带宽为256 MHz。忽略频率捷变过程中出现的频点丢失和频点重复，理论上最小分辨率为0.586 m。对于雷达而言，合作目标相当于一个点。

图8为采用随机频率捷变信号处理后得到的一维距离像结果，共有3个点目标，其中中间为标校球，其余为栅瓣。从结果中可以看出，采用上述处理方法能合成一维距离像，实现了合成高分辨，分辨率达到1 m左右。受频率随机性影响，捷变间隔不固定，合成后的一维像受栅瓣影响。

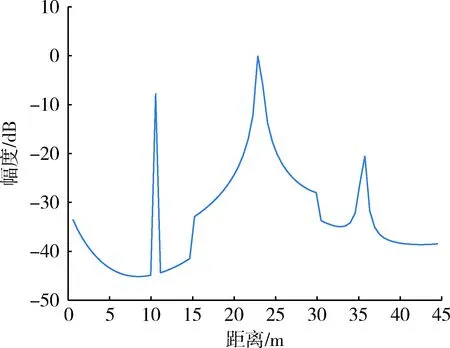
图8 标校球一维距离像Fig.8 One dimensional range profile of calibration sphere

6 结束语

针对现有窄带雷达分辨率不高的问题，结合雷达的抗干扰特性，分析了利用窄带雷达随机频率捷变信号进行成像的可能性。针对随机捷变信号，给出了信号处理方法，分别通过理论仿真和实装数据进行了验证。验证结果表明，可实现对窄带雷达随机捷变信号进行成像处理，提高了窄带雷达的距离分辨能力。由于目前研究还处于对数据进行事后处理阶段，且目标为标校球，散射点固定，处理方法相对简单。后期，可结合民航飞机进行成像处理，优化多散射点目标的处理算法，进一步提高窄带雷达的工程应用能力。