基于双柱的小型无人机极化信道模型特性研究*

骆泽群，王永川，闫云斌

(陆军工程大学石家庄校区，河北 石家庄 050003)

0 引言

多输入多输出(multiple input multiple output,MIMO)技术以其大容量、高质量传输性能优势成为无线通信的一项重大突破[1-2]，所以应用MIMO技术到小型无人机数据链[3]为解决目前小型无人机有限的通信性能提供了新的途径。因此，针对小型无人机的MIMO信道模型的研究是实现小型无人机稳定高速通信的关键。

MIMO系统的一个问题就是需要大的天线间隔以求获得足够低的天线间相关性，并且已经提出极化MIMO系统作为减小终端所需间隔的解决方案。

多极化天线系统[4-5]能够在保持低天线间相关性的同时减小设备尺寸，因此对于小型无人机的无线通信系统具有很大的潜力。与单极化天线相比，多极化天线系统利用极化自由度，显著增加信道容量[6]。

信道去极化[7-8]对多极化MIMO信道的性能有着重要的影响，引起了人们的广泛关注，同样在小型无人机空地通信信道中也存在着影响，本文以基于双柱的小型无人机空地极化信道为例阐述。

发射机(TX)和接收机(RX)之间的信道去极化主要是由通过散射物体到达RX的平面波引起的，信道极化函数被广泛地用来表示信道去极化。无线电信道可以用4个正交极化函数fVV，fHV，fVH和fHH来描述，其中H和V分别指水平极化和垂直极化。去极化的程度通常是用交叉极化鉴别率(cross polarization discrimination,XPD)来衡量的，一些论文基于信道测量研究了XPD[9]。然而，上述工作并不能为信道去极化的仿真提供一个严密的数学模型。在文献[10]中，提出了一种基于几何理论的窄带信道去极化参考模型，可用于XPD的定量计算。然而，这项工作仅限于单输入单输出(SISO)系统，不能用于多极化多输入多输出(MIMO)系统。

为了更好地解决MIMO信道去极化问题，本文利用基于几何的双柱三维MIMO统计模型导出了信道极化函数。本文采用文献[10]中的方法，并对其推导方法进行了改进，并将其推广到一般的MIMO场景中。

1 极化MIMO信道模型

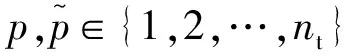
如图1所示，散射体产生3种不同的传播模式：LOS模式，其中波直接从TX传播到RX，在TX侧(SBT)模式单次反弹，其中波在到达TX之前从位于TX周围的散射体散射。在RX侧(SBR)模式下单次反弹，其中波在到达RX之前从位于RX周围的散射体散射。因此，信道脉冲响应可以表示为LOS，SBT以及SBR射线的叠加。图中参数在表1中做出了说明。

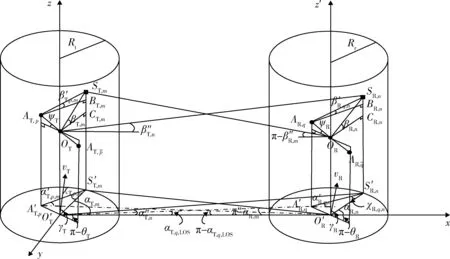
图1 基于双柱的无人机城市信道模型Fig.1 Channel model of UAV urban based on two cylinders

图2显示了SBT模式，其中从TX发射的垂直极化平面波V可以导致在RX处接收的水平极化平面波。V′是从散射体ST,m反射后的相应极化矢量，它不是完全垂直极化并且具有交叉极化分量，如图2所示。这种现象是信道去极化，并且它取决于图2中的角度和图1中的其他参数。这里我们将TX，RX和散射体定义的平面命名为极化守恒平面，如文献[10]中所说的那样，θV是V和包括V投影到极化守恒平面上的线之间的角度。考虑来自TX的垂直极化平面波。通过使用文献[10]中的极化守恒平面的几何结构，可以获得对于p-q链路和TX侧的第m个散射体，SBT信道极化函数可以如下获得

(1)

(2)

式中：|·|表示绝对值。cosφ6和cosφ7可以通过使用余弦定律并将文献[10]中的推导与图1和图2中的三维MIMO场景的几何结合来获得。如下所示

cosφ1=

(3)

cosφ2=

(4)

(5)

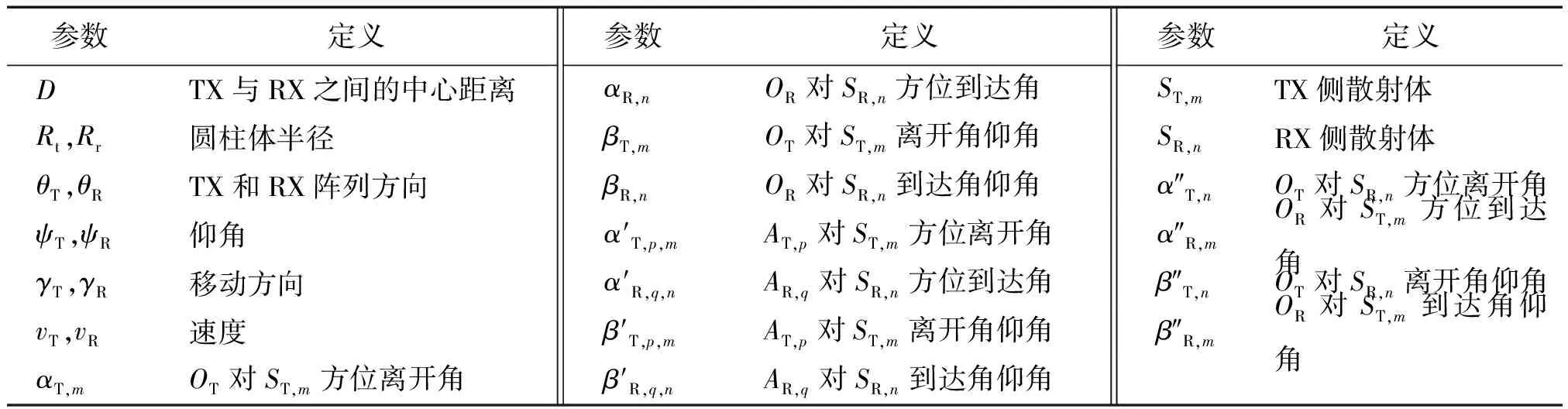
表1 参数定义Table 1 Parameter definitions

图2 SBT模式Fig.2 SBT mode

cosφ4=

(6)

(7)

(8)

(9)

对于上述等式，距离ε可以通过使用余弦定律和图1和图2中的几何模型来计算。利用导出的信道极化函数，可以获得用于SBT MIMO场景的XPD。

2 交叉极化鉴别率

XPD测量了传播环境的去极化现象，是双极化系统建模的基本参数[11]。p-q链路的平均XPD定义如下

(10)

式中:PVV,pq和PHV,pq分别为通过VV和HV通道的接收功率。值得注意的是，当M,N→∞时，离散出发和到达角(在方位角和仰角域上)可以用具有联合概率密度函数的连续随机变量代替[10]。因此，可以有

(11)

式中：AV,pq为从垂直极化平面波散射后接收的极化矢量的幅度。

对于方位角分布，使用von Mises分布，由于它近似于许多经典分布，因此被广泛采用[12]。对于仰角分布，使用文献[13]中的余弦分布。角分布的概率密度函数表示为

(12)

(13)

3 仿真结果分析

在本节中，基于上述推导，对SBT模式下参考模型的散射体角分布参数对信道去极化的影响进行了仿真实验，并进行数值分析。基于文献[10，15]考虑以下SBT情形。

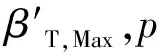
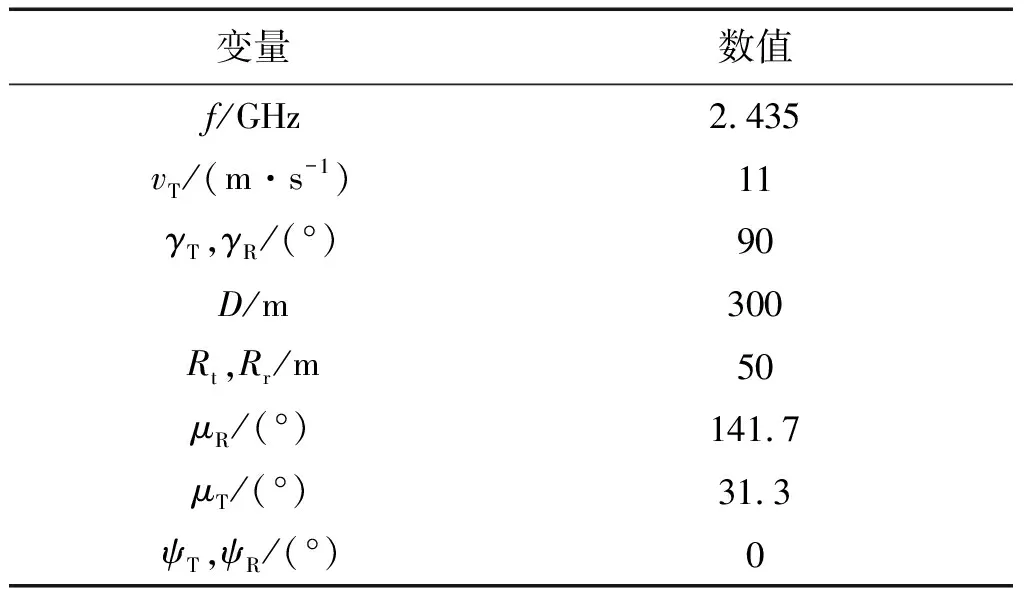
表2 城市环境参数Table 2 Urban environmental parameters

θT=θR=90°图3 SBT模式的XPD随kT变化曲线Fig.3 XPD versus kT for the SBT model

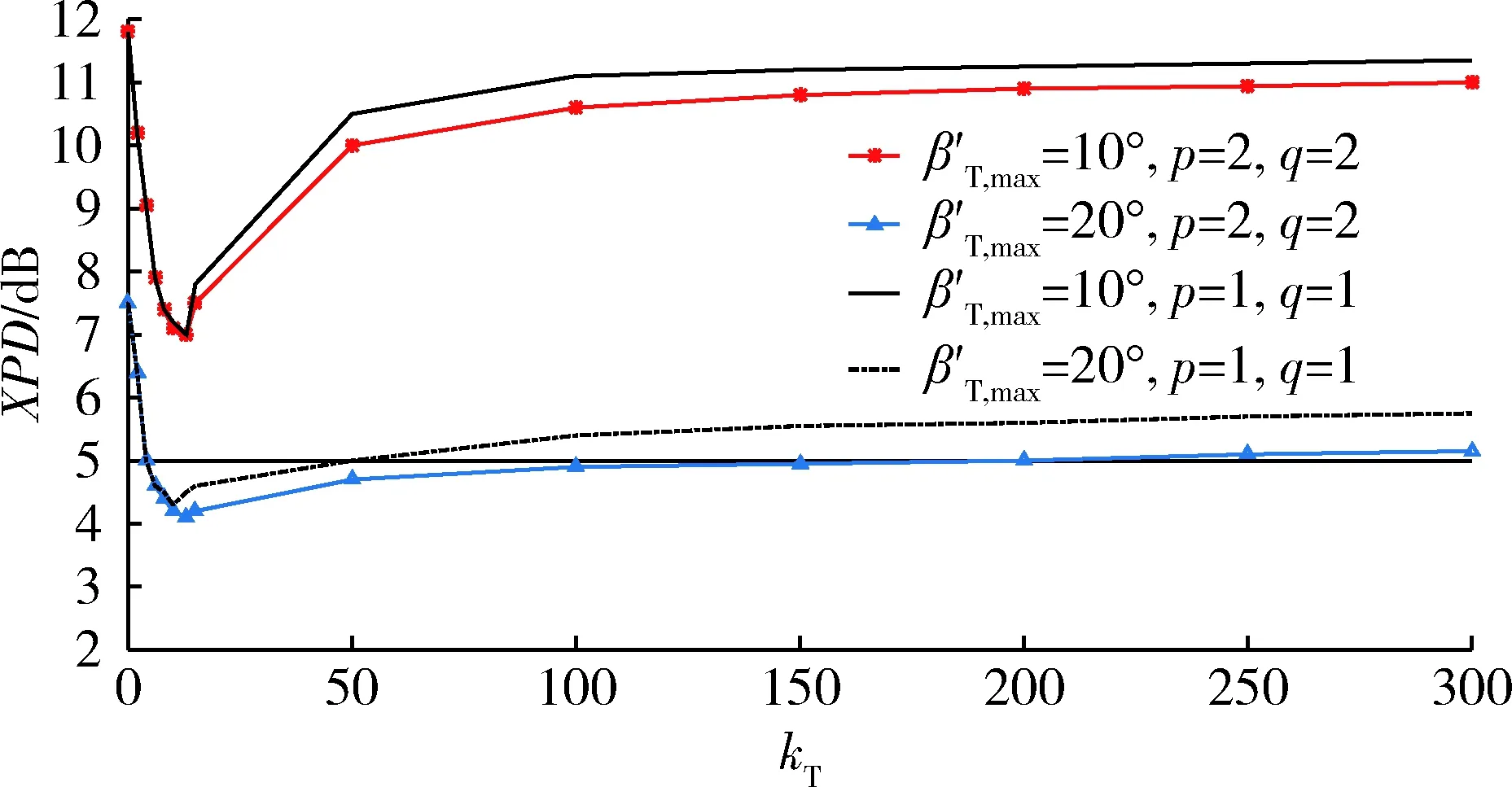
θT=90°且θR=270°图4 SBT模式的XPD随kT变化曲线Fig.4 XPD versus kT for the SBT model

4 结束语

本文提出了一种基于双柱的极化MIMO信道几何参考模型。在模型推导中考虑了信道去极化的机理，提出了计算MIMO信道XPD的解析方法。详细讨论了双柱极化MIMO模型的SBT模型，并对角参数对XPD的影响进行了数值分析。研究发现，极化MIMO信道不同于极化SISO信道，由此产生的XPD取决于MIMO子信道和其阵列方向，因此，在小型无人机天线系统设计中对天线阵列应当予以考虑。