多燃气发生器多时序点火优化技术*

刘少伟，关娇，时建明，苗海玉

(空军工程大学a.防空反导学院；b.信息与导航学院，陕西 西安 710051；c.航空机务士官学校，河南 信阳 464000)

0 引言

导弹冷弹发射一般是通过火药在高压室内燃烧产生高温高压燃气，经过喷管膨胀降压，进入低压室，建立低压室压强，作用在承压面上形成弹射力将导弹弹射出去[1-3]。随着导弹型号的不断增加，导弹混装、共架发射技术已在世界主要军事强国得到广泛应用，在自力热发射方面，美国海军的MK-41垂直发射系统采用模块化设计，可以发射“标准”、“海麻雀”、“战斧”、“阿斯洛克”等十几种型号的导弹，执行包括对地攻击、防空反导在内的多种作战任务，是通用热发射的典型代表[4]。在冷弹发射方面，由于各型导弹质量、最大承受过载等技术指标不同，多种型号导弹很难实现弹射装置的通用化，例如不能使用C-300导弹弹射器发射“道尔”导弹，因为导弹弹射过程承受过载和导弹运动速度不能满足技术指标要求[5]。文献[6]提出远射程火炮模块化装药的思想，文献[7]提出使用多个燃气发生器和1个点火控制组合组成的通用导弹弹射器，燃气发生器采用模块化设计，具有相同的结构参数和装药参数。针对不同弹型，通过增减燃气发生器个数、调整各个燃气发生器接力点火的时序实现导弹出筒过程小过载、大速度的指标要求，但文献[7]未进一步说明点火时序如何确定。对于多燃气发生器点火时序的确定，凭借经验或多次调整时序参数，可以得到满足导弹过载要求和速度要求的内弹道参数，但是不一定达到最高的低压室压强利用率，导致弹射器的性能不一定是最佳的。文献[8-12]对导弹弹射器的内弹道特性进行了仿真研究，在此基础上，建立多燃气发生器弹射内弹道模型，提出多燃气发生器点火时序优化算法，旨在解决如何用最优的多燃气发生器点火时序实现满足过载要求的最高的低压室压强利用率。

1 多燃气发生器弹射内弹道模型

1.1 多燃气发生器结构

图1为本文设想的双提拉杆式弹射器多个燃气发生器安装示意图，在发射筒导轨下面并排安装若干个燃气发生器，不会造成随着燃气发生器数目增加引起发射筒直径增加的问题，每个燃气发生器通过各自的弯管将高温高压燃气导入作动筒，高温低压燃气在作动筒内持续做功，推动活塞向上运动，活塞带动活塞杆、活塞杆带动提弹梁、提弹梁托着导弹向上运动。

图1 多燃气发生器弹射装置示意图Fig.1 Structure diagram of ejection device with multi-gas generators

1.2 基本假设

高压室内弹道数学模型的相关假设[13]：

(1) 在一定点火压力下，装药被瞬时、全面点燃，装药的燃烧服从几何燃烧定律；

(2) 由于高压室内气流流动速度远小于喷管中气流流动速度，认为燃气在高压室内无流动，各处的压力、密度、温度等是均匀的；

(3) 高压室内燃气按理想气体处理；

(4)认为燃气的成分、物理化学性质是固定不变的，爆温T0、比热Cp、绝热指数k等按常量处理；

(5) 在高压室内，火药燃烧过程是绝热的，与室壁没有热交换；

(6) 在装药燃烧阶段，高压室燃气温度变化不大，可以认为高压室燃气温度T1是常量，其大小等于散热修正后的定压燃烧温度，即T1=χ1T0。

低压室内弹道数学模型的相关假设：

(1) 低压室内燃气按理想气体处理；

(2) 认为燃气的成分、物理化学性质是固定不变的，爆温T0、比热Cp、绝热指数k等按常量处理；

(3) 不考虑低压室内压力的空间分布，而是采用瞬时平均压力；

(4) 以系数χ2对低压室内的总温进行修正，主要考虑低压室与外界的热交换损失。

1.3 第i个高压室弹射内弹道模型

(1) 燃速方程

(1)

式中:ei为装药当前时刻厚度;a为燃速系数;n为燃速指数;p1i为高压室压强。

(2) 燃面变化方程

假定使用增面燃烧火药，燃面变化方程为

(2)

式中:si为装药当前时刻燃烧表面积;Ni为装药根数;Li为装药长度。

(3) 燃气生成速率方程

(3)

式中:ω为高压室装药初始质量;ψi为装药当前时刻燃去比例;ui为燃烧速度;ui=dei/dt;γ为装药密度。

(4) 高压室流量方程

(4)

式中:Y1i为当前时刻由高压室流向低压室的燃气总质量；Ti1为当前时刻高压室温度；skp1为高压室喷口面积；R为气体常数；k为比热比；p2为当前时刻低压室压强。

(5) 高压室压强变化方程

(5)

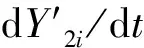
1.4 低压室主要弹射内弹道模型

(1) 低压室压强方程

(6)

式中:W2为低压室初始容积;sp为低压室承压面积;lm为当前时刻导弹行程。

(2) 低压室反流流量方程

当低压室压强大于高压室i压强时，燃气由低压室流入高压室i，燃气流量为

(7)

式中:T2为当前时刻低压室温度。

(3) 低压室温度方程

(8)

式中:vm为当前时刻导弹速度。

(4) 导弹行程方程

(9)

(5) 导弹速度方程

(10)

式中:m为弹射总质量;f为摩擦力。

1.5 多时序点火弹射内弹道数值解法

弹射内弹道求解问题的实质是求解常微分方程组，运用常规解析方法求解比较困难，通过计算机进行数值积分计算是求解弹射内弹道问题最有效的方法。在已知装填条件和弹射器内部结构诸元的条件下建立内弹道方程组，通过求解微分方程组得到内弹道的数值解。从实用、精度、方便性及掌握程度等几方面考虑，可以选用定步长的四阶龙格-库塔法求解弹射器内弹道问题。

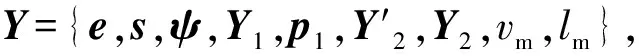
(11)

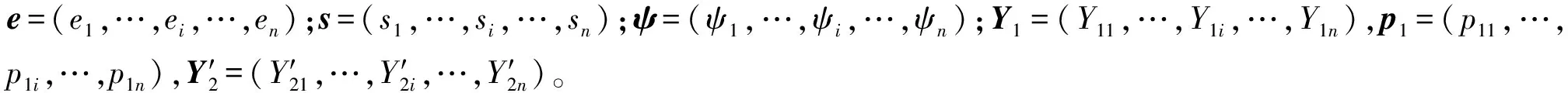
利用经典四阶龙格库塔法进行求解：

(12)

式中:h为仿真步长。在每次迭代过程中，利用得到的Yk+1求解低压室压强p2和温度T2。

求解步骤如下：

第1步 设置仿真步长h，装药质量ω，装药内径di(i=1,2,…,n)，装药外径Di(i=1,2,…,n)，装药个数Ni(i=1,2,…,n)，装药燃速系数a，压力指数n，气体常数R，高压室喷口面积Skp1、低压室泄压口面积Skp2，高压室初始容积W1i(i=1,2,…,n)，低压室初始容积W2、低压室承压面积sp、弹射质量m等参数。

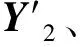
2 多燃气发生器点火时序优化算法

对于固定点火时序，可以通过上一节给出的多时序点火弹射内弹道数值解法计算高压室压强、低压室压强、喷口流量、弹体速度、弹体行程等随时间变化的内弹道参数，本节提出的点火时序优化算法以多时序点火弹射内弹道数值解法为基础计算目标函数值。

粒子群算法属于进化算法[14-15]，可以从随机解出发，通过迭代寻找最优解，适用于多个连续变量的优化问题。在粒子群系统中，每个备选解被称为一个粒子，多个粒子合作选优，每个粒子根据它自身的经验和相邻粒子群的最佳经验在问题空间中向更好的位置飞行，搜索最优解。本文中多个燃气发生器的点火时刻采用粒子群算法进行优化。

(1) 适应度函数

由于采用模块化高压室，主要考虑低压室弹射力做功的效率，在弹射过程中低压室最大压强为p2g，导弹最大加速行程为lg，以p2g和lg构成的矩形面积为基准，利用p2-lm曲线下面积充满该矩形面积的程度(充满系数)作为主要目标函数，如图2所示。

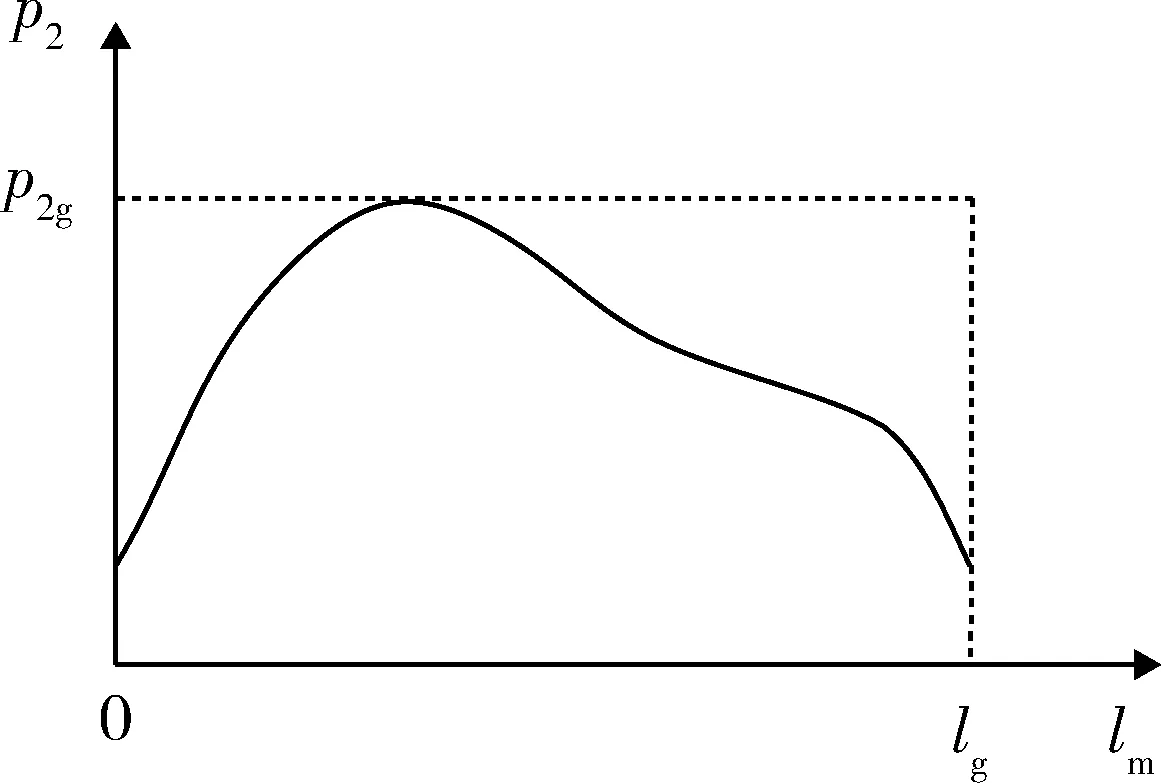
图2 充满系数示意图Fig.2 Diagram of fullness coefficient

对于不同导弹，要求过载指标值不同，如果已知某型导弹指标规定的低压室最大压强为ptarget2，在优化过程中，如果p2g大于ptarget2，需要在优化算法中以惩罚的形式加以考虑。目标函数如下

(13)

式中:ti为高压室i点火时刻；η为惩罚系数。

(2) 位置速度更新方程

假设在n维(n代表燃烧室个数)搜索空间中有m个粒子，第i个粒子的位置向量为ti=(ti1,ti2,…,tin)T,速度为vi=(vi1,vi2,…,vin)T。个体极值向量为pi=(pi1,pi2,…,pin)T，整个粒子群的最优极值向量为pg=(pg1,pg2,…,pgn)T。按照追随当前最优粒子的原理，粒子按照式(14)改变位置和速度：

(14)

式中：r1，r2为[0,1]之间的随机数；c1,c2为加速度系数；ω为惯性权重。

3 算例分析

本文采用模块化燃气发生器(具有相同装药参数、相同高压室结构)，分别比较了单个高压室、2个高压室及3个高压室条件下的弹射内弹道性能。单个高压室的情况只采用本文提出的多时序点火弹射内弹道数值解法，不使用点火时序优化算法(只有一次点火)，2个高压室及3个高压室的情况采用点火时序优化算法。

(1) 单个高压室情况

点火时刻设置为0，导弹运动到2.3 m开始泄压，运动到2.6 m导弹加速行程结束，弹射内弹道模型解算采用本文提出的多时序点火弹射内弹道数值算法，计算步长为0.001 s，计算得到高压室压强-时间曲线p1-t(图3a))、低压室压强-时间曲线p2-t(图3b))、导弹行程-时间曲线lm-t(图3c))、导弹速度-时间曲线vm-t(图3d))，低压室压强-导弹行程曲线p2-lm(图3e))。

说明如下：

1) 从高压室曲线p1-t中可以看出，把火药全面燃烧时的压力4.5×106Pa作为初始压力，燃烧开始阶段压力呈现平缓上升趋势，压力达到最大值2.96×107Pa，这主要原因是高压室采用增面燃烧火药。

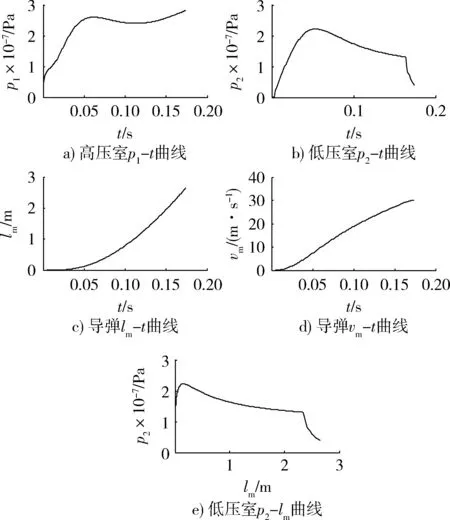
图3 单个高压室条件下内弹道曲线Fig.3 Interior ballistic curve of single high-pressure chamber

2) 从低压室p2-t曲线中可以看出，由于高压室高温高压燃气通过喷孔流向低压室，低压室压强p2不断上升，低压室最高压强达到p2=2.27×107Pa，然后呈平缓的下降趋势，这是由于随着导弹速度的增大，低压室容积越来越大。从低压室p2-lm曲线可得出低压室压强利用效率为0.681。在t=0.17 s左右，通过导弹行程lm-t曲线得出，此时导弹行程为lm=2.3 m，导弹最大速度vm=30.7 m/s。

(2) 2个高压室的情况

高压室装药参数与算例1一致，高压室1的点火时刻设置为0时刻，高压室2的点火时刻作为优化变量，低压室最大允许压强为2.4×107Pa，导弹运动到2.3 m开始泄压，运动到2.6 m导弹加速行程结束。弹射内弹道模型解算采用本文提出的多时序点火弹射内弹道数值算法，计算步长为0.001 s；时序优化算法采用本文提出的多燃气发生器点火时序优化算法，邻域搜索区间为0.001 s。优化算法得到高压室2的点火时刻为0.067 8 s，即高压室1在0时刻点火、高压室2在0.067 8 s点火，低压室压强利用效率为0.881，导弹最大速度vm=34.5 m/s。计算得到高压室压强-时间曲线p1-t(图4a)、图4b))、低压室压强-时间曲线p2-t(图4c))、导弹行程-时间曲线lm-t(图4d))、导弹速度-时间曲线vm-t(图4e))、低压室压强-导弹行程曲线p2-lm(图4f))。

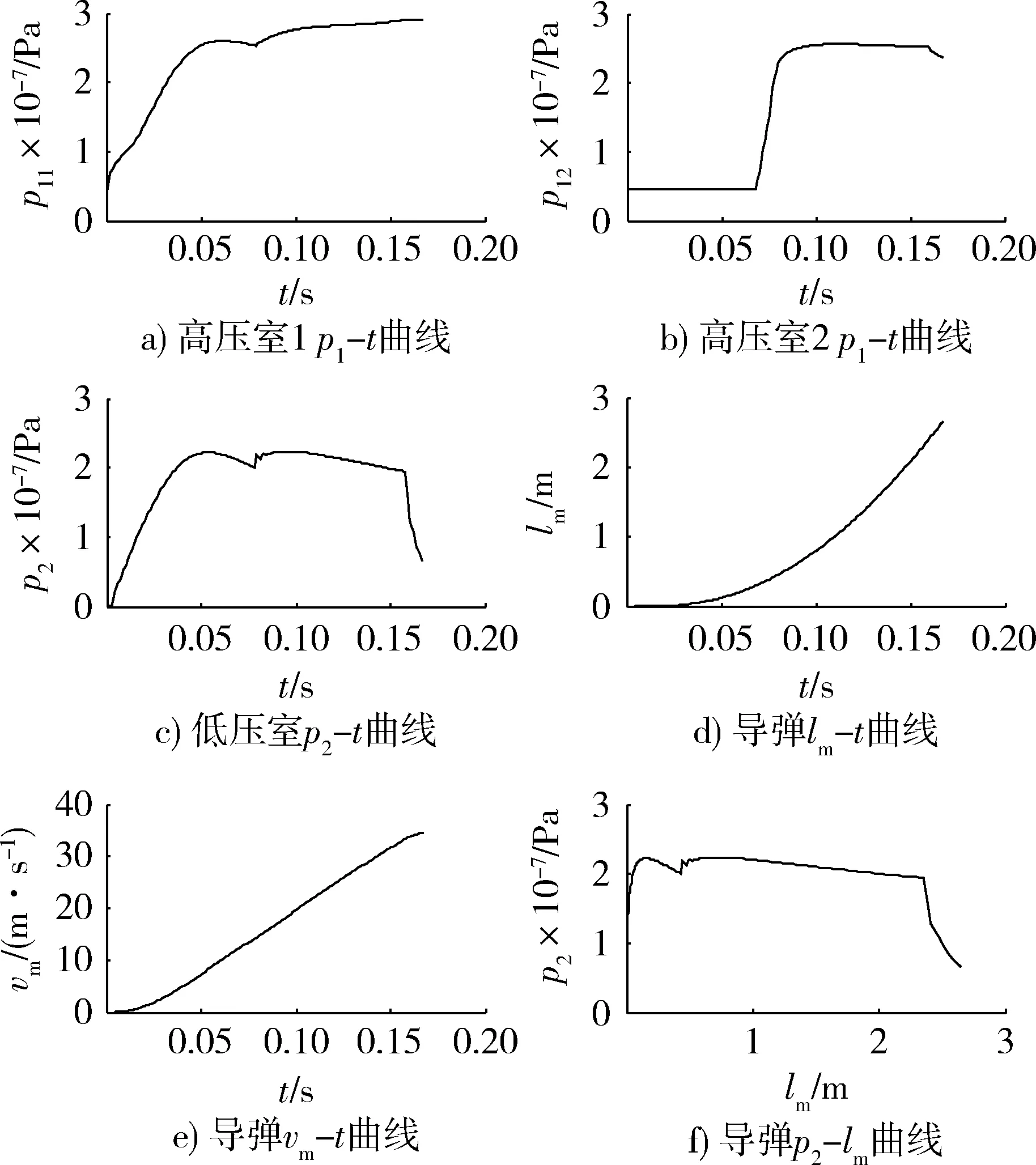
图4 两个高压室条件下内弹道曲线Fig.4 Interior ballistic curve of two high-pressure chambers

(3) 3个高压室的情况

高压室装药参数与算例1一致，高压室1的点火时刻设置为0时刻，高压室2的点火时刻、高压室2的点火时刻作为优化变量，低压室最大允许压强为2.4×107Pa，导弹运动到2.3 m开始泄压，运动到2.6 m导弹加速行程结束。弹射内弹道模型解算采用多时序点火弹射内弹道数值算法，计算步长为0.001 s；时序优化算法采用多燃气发生器点火时序优化算法，邻域搜索区间为0.001 s。

优化算法得到高压室2的点火时刻为0.066 s，高压室3的点火时刻为0.115 s，即高压室1在0时刻点火、高压室2在0.066 s点火，高压室3在0.115 s点火。低压室压强利用效率为0.922，导弹最大速度vm=35.8 m/s。计算得到高压室压强-时间曲线p1-t(图5a)～c))、低压室压强-时间曲线p2-t(图5d))、导弹行程-时间曲线lm-t(图5e))、导弹速度-时间曲线vm-t(图5f))、低压室压强-导弹行程曲线p2-lm(图5g))。

图5 两个高压室条件下内弹道曲线Fig.5 Interior ballistic curve of three high-pressure chambers

通过以上算例说明，采用单个、2个、3个燃气发生器(其中2个和3个燃气发生器采用本文的优化算法优化点火时序)，在相同的导弹行程条件、相同的低压室最大压强约束下提高了低压室压强利用效率，分别为0.681，0.881，0.922，也提高了导弹的出筒速度，分别为30.7，34.5和35.8 m/s。

4 结束语

本文基于多燃气发生器、多时序点火、模块化装药的通用弹射思想，利用经典弹射内弹道理论建立通用弹射模型，在弹射加速度和速度指标确定的条件下，建立考虑导弹最大过载和低压室推力效率的目标函数,提出多燃气发生器点火时序优化算法，通过改变燃气发生器的点火时序，实现符合指标要求的导弹通用弹射。通过3种仿真情况的比较，验证了多燃气发生器弹射器较单燃气发生器弹射器有更好的弹射性能(如更高的出筒速度、更大的低压室压强利用率)，也验证了多燃气发生器点火算法的有效性。