粒子群优化算法对吸波结构材料优化研究*

郑日升，张春林

(1.北京电子工程总体研究所，北京 100854；2.陆军北京军事代表局驻北京地区军事代表室，北京 100854)

0 引言

为提高飞行器的突防能力和生存能力，现代的飞行器都采用气动外形隐身和材料隐身降低飞行器的雷达散射截面(radar cross section，RCS)。吸波结构材料是材料隐身技术一种有效的方法，将吸波剂加入到复合材料中，不仅具有电磁波吸收能，而且不会受到结构受力的材料的影响[1]。

吸波结构隐身材料都要求反射率低，吸波能力强，阻抗匹配效果好，要求相应的材料具有隔离层厚度薄，而且质量小等特点[2]。随着研发技术的不断进步，已经有多种新型吸波结构隐身材料被应用于各种飞行器中，在军事领域也得到了大量的应用[3]。在目前研制的新型材料中具有各向异性特性的材料也开始得到应用[4-7]。典型的美国隐身飞行器如F-22，在翼面和进气道等区域采用了高性能吸波结构复合材料，有效地减缩了飞行器的RCS值[8-9]。以频率点上的反射率作为优化目标函数，获得了多层吸波结构材料的优化设计方法[10]。在研发新型材料过程中，大量的优化算法也应用于材料参数优化中。遗传算法具有全局最优的搜索能力，因此在材料优化中应用较为广泛，为材料测试提供了基础。文献[11-12]以天线罩壁等效平板结构为优化目标，频率为600 MHz,针对多层介质的厚度进行优化，并得到了较好的优化效果。文献[13]基于几类典型材料,以吸收频带宽为目标,在给定厚度下对RAM进行了优化设计。文献[14-15]优化得到的吸波材料具有频带宽、厚度薄的特点,获得了较好的优化效果。本文首先基于吸波结构材料隐身特性，采用粒子群算法和遗传算法，针对三层吸波结构隐身材料进行优化研究。

1 吸波结构材料反射率计算方法

1.1 反射率计算方法

图1是典型的Jaumann多层吸波结构，其中金属板在最底层，在底板上层是厚度d(mm)和电阻抗R2(Ω)。

其中，各层吸波材料的输入阻抗可由式(1)得到：

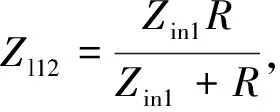
(1)

其中:R为电阻；Zin1为输入阻抗，Zl12为负载阻抗，即任何一个电气元件都有一定的阻抗，相对于电源而言，该阻抗就是负载阻抗。

多层吸波材料对电磁波的反射特性可由功率反射率(简称反射率T)由下面2个计算公式得到：

(2)

P为反射系数，转化为反射率T公式为

T=20lg|P|.

(3)

1.2 单层Salisbury吸波屏反射率研究

下面是针对Salisbury吸波屏反射率进行分析，Salisbury吸波屏是指单层吸波材料放到金属基体上。单层吸波材料隔离层厚度为1/4隔离层介质波长，即7.5E-3 mm，电阻R=377 Ω的反射率，频率带宽2～18 GHz，从图2中可以看出，反射率T在入射频率约10 GHz时反射率最小，但是频率带宽较窄。目前，对于结构型吸波材料很少采用Salisbury吸波屏，主要是单层吸波结构材料频带较窄，不适用于现在宽雷达频率捕捉范围，在工程方面单层吸波屏已很少采用。

基于以上的分析，下面针对3层Jaumann吸波结构材料进行初步分析，对电阻抗，隔离层厚度和介电常数进行优化研究，文章以吸波材料的频宽为目标函数，针对粒子群优化算法构造目标函数。

2 粒子群优化算法目标函数构造

实际上各层吸波材料的介电常数ε、电阻抗R、介质的厚度d均是频率的某种函数关系，所以反射率就是关于介电常数、材料电阻和各层厚度的函数，可记为

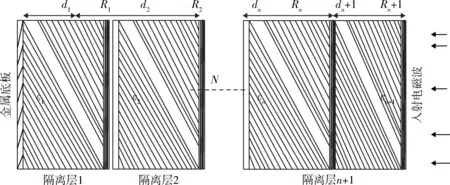
图1 多层吸波结构材料简化图Fig.1 Sketch of multi-layer absorbing structure material

Z=F(ε，R，d1，d2，…，dn)，

(4)

式中：Z为材料的不同组合方式。

考虑在频率区间[fa,fb]上的反射率曲线，当多层吸波材料在指定频率区间内达到最佳吸波效果时，得到相应的材料参数，本文取反射率T<-15 dB条件下，反射率总和取最小值，即反射率曲线与频率轴围成的区域的面积应是最小值，如图3所示。

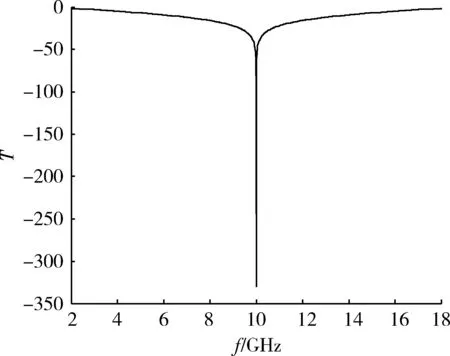
图2 单层Salisbury反射率Fig.2 Single Salisbury reflectivity

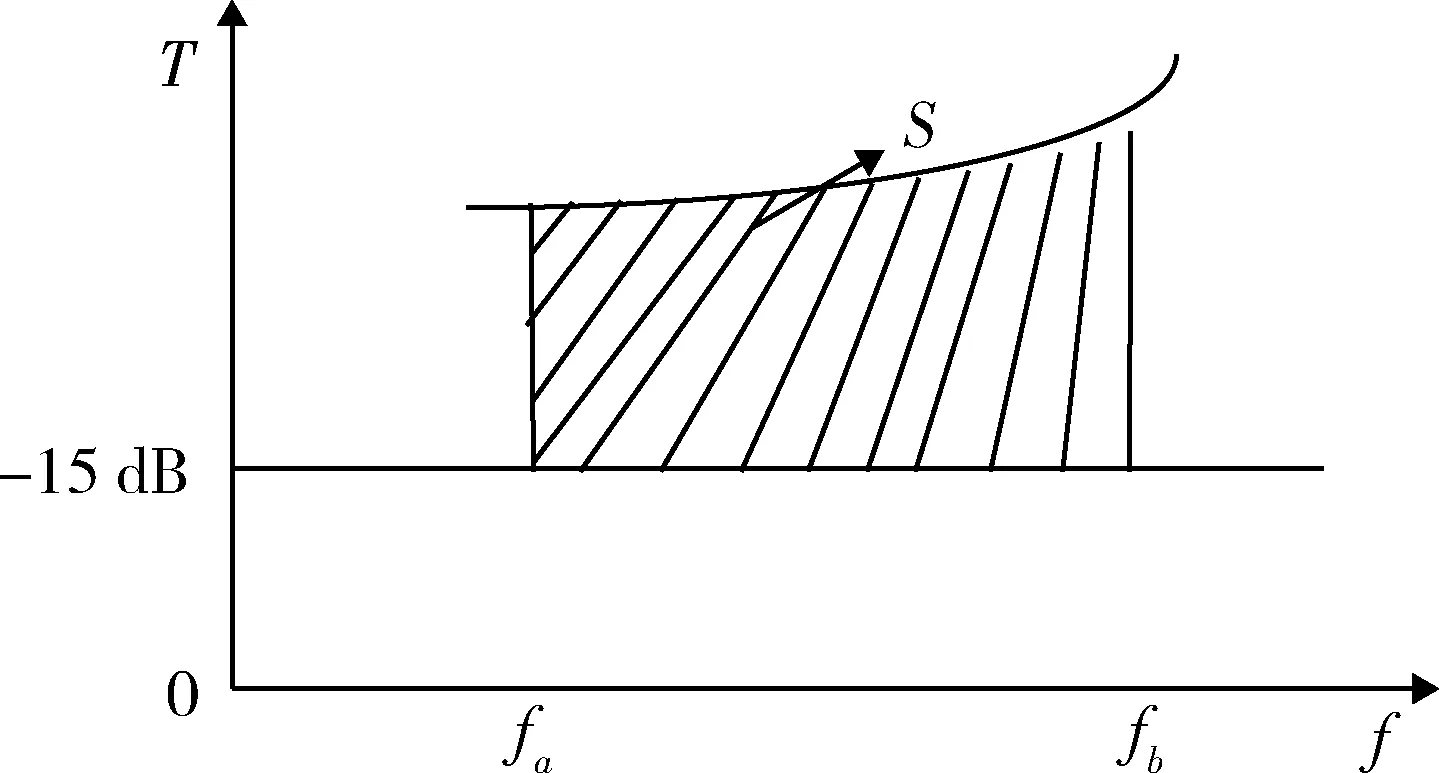
图3 吸波材料的反射率总和面积示意图Fig.3 Sketch of the reflectivity of absorbing structure material

令

诗与词是有区别的。二者形式上的区别显而易见：诗，尤其是近体诗，或七言或五言，或仄起或平起，整齐而规则；词就不一样了，几百个词牌子，常用的也有几十个，长的百余字，短的几十字，句子长短不一，用韵宽，有的一韵到底，有的还中间转韵，比如《菩萨蛮》。

,

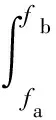
(5)

则求面积S的极小值内的频率带宽为目标函数，即确保T<-15 dB条件下，在频带宽内的反射率面积最小。

3 粒子群优化算法和遗传算法介绍

3.1 粒子群优化算法

首先将粒子群优化算法应用到多层吸波材料优化设计，将所要求频带内整体反射率最小，将反射率T<-15 dB条件下的频率带宽为目标函数，在指定吸波材料厚度和电阻以及介电常数约束的情况下，准确计算出最优的多层吸波材料组合。由于多层吸波结构材料目标函数是求解一个极值问题，因此可以用粒子群优化算法来优化研究。

粒子群优化算法基本流程可描述为：

(1) 初始化：随机生成M个粒子Xi和速度vi，当前最佳位置Pbesti=(Pbesti1,Pbesti2,…,Pbestin)得到粒子的初始种群t0。

(2) 给定参数：惯性因子ω，加速因子C1和C2，种群大小N，最大迭代次数Dmax。

(4) 进化出新的粒子：由上述列出的PSO粒子生成M个新粒子。

(5) 目标粒子的选择：计算粒子群t1中的粒子的适应度值，若该粒子适应度值比父代差，则抛弃，否则保留该粒子形成新一代粒子群体。

(6) 是否结束运算，若满足所求问题的要求或已达到最大迭代次数，则终止搜索，否则继续进入循环迭代，更新粒子。

3.2 遗传算法

遗传算法采用比例选择方法，单点交叉算子作为交叉算子，选用基本位变异算子作为变异算子。基于遗传算法的多层吸波材料优化初始参数设置为：种群大小M为600，运行代数迭代范围为0～600，交叉概率G为0.10～0.99，变异概率G1为0.001～0.100。

4 吸波结构材料优化

基于以上分析，本算法定义种群数量为0～600，种子数越多，越有可能收敛到全局最优值，但算法收敛速度慢。频率范围2～18 GHz，以0.01 GHz为间隔的速度向目标移动，最大速度取变化范围的10%～20%，该范围越小，收敛的分辨率越高，即不容易跳过最优值，但收敛慢；越大，收敛速度快，但可能跳出全局最优值。由于粒子群优化算法比遗传算法更为简单，没有遗传算法的交叉和变异操作，受到约束的变量较少，没有许多参数需要调整。图4和图5表示粒子群优化算法和遗传算法连续3次优化计算的反射率结果，发现连续3次优化结果相近，也就是说，粒子群优化算法能够一次计算就能够得到全局最优解。而遗传算法3次优化得到的反射率具有较大的区别，稳定性差。

图4 粒子群优化算法连续3次优化计算结果Fig.4 Results of the optimization with three consecutive of PSO algorithm

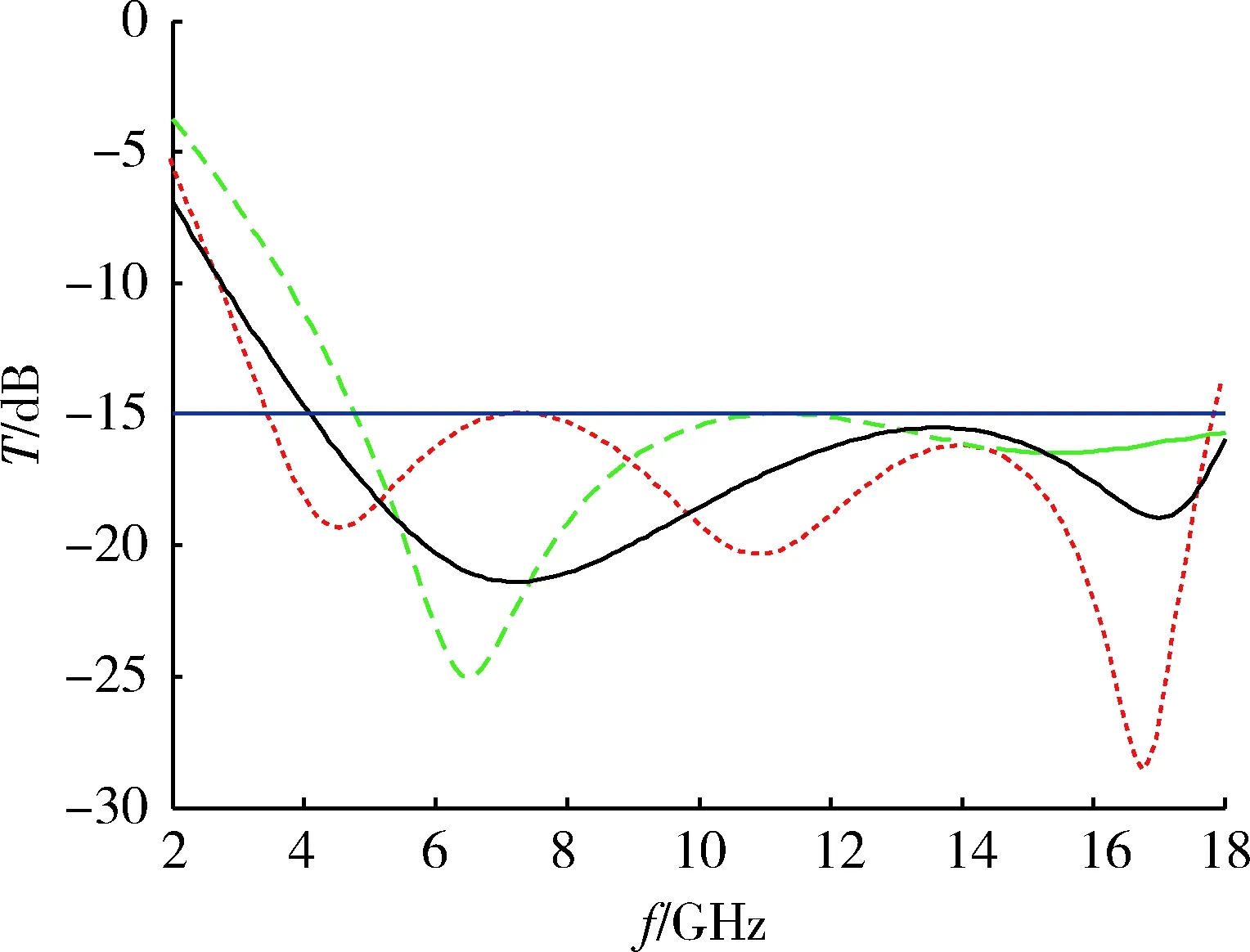
图5 遗传算法连续3次优化计算结果Fig.5 Results of the optimization with three consecutive of genetic algorithm

下面是遗传算法和粒子群优化算法针对2层吸波材料在反射率T<-15 dB条件下，频率带宽的优化结果。通过频带宽发现，粒子群优化算法比遗传算法频带宽约2 GHz。通过图6中也可以发现，粒子群优化算法在不同频率反射率总和也相对较小。

下面采用2种算法针对3层吸波材料反射率T<-10 dB进行优化比较，从图7中发现，在2～8 GHz 2种算法反射率接近，整个频率范围内只有在2 GHz-10 dB。

接下来比较了反射率T<-20 dB条件下2种优化算法频宽，相比图8得到的结果发现，2种优化算法频宽有较大的区别，在反射率相同的条件下，采用粒子群优化算法得到的频宽比遗传算法要大3 GHz，表明采用粒子群优化算法能得到较宽的频宽。

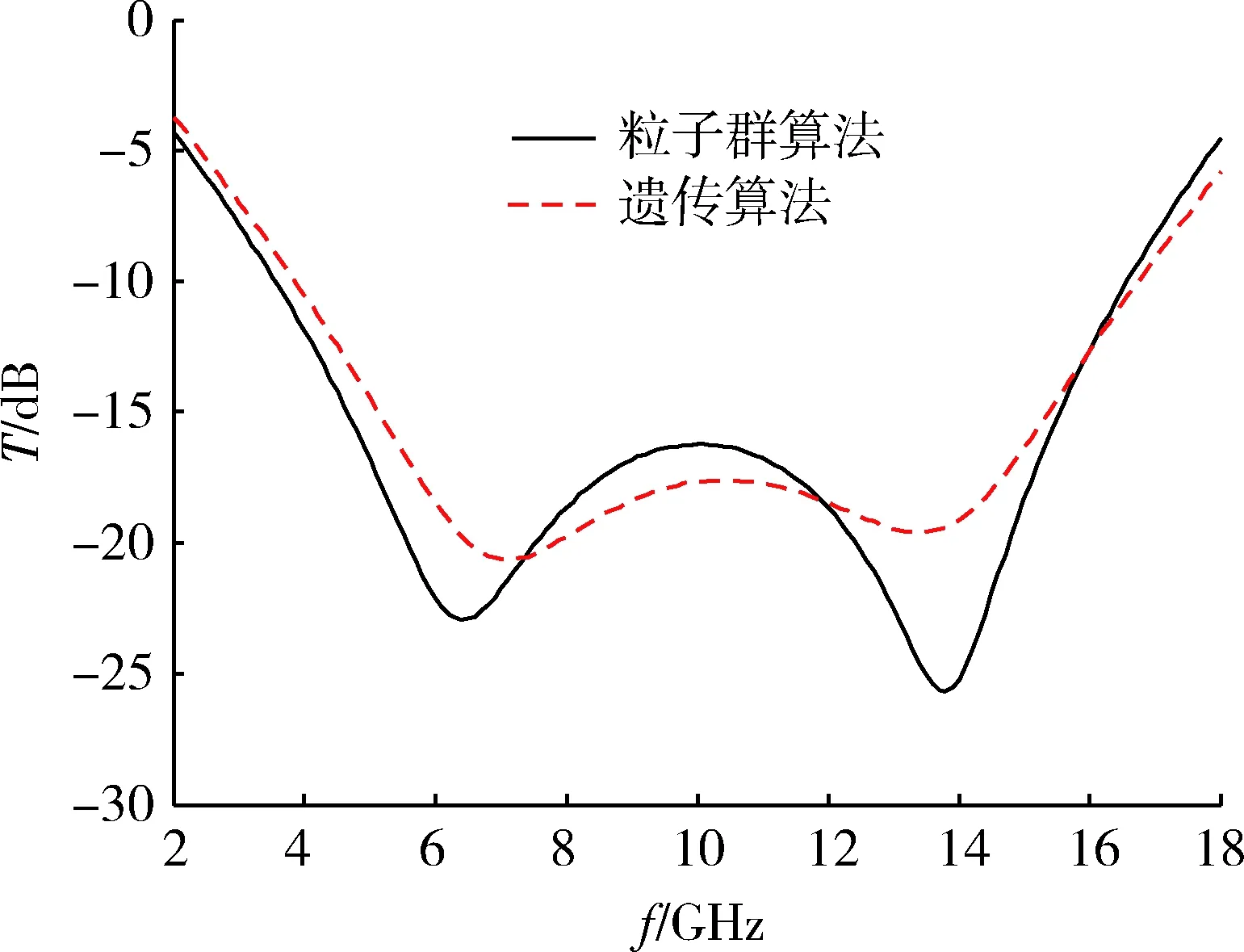
图6 两层吸波材料反射率T<-15 dB 2种优化 算法结果比较Fig.6 Comparison of two optimization algorithms for two layers of absorbing materials with reflectivity of T<-15 dB

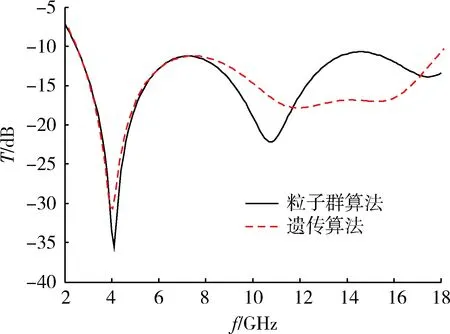
图7 三层吸波材料反射率T<-10 dB 2种 优化算法分析Fig.7 Comparison of two optimization algorithms for three layers of absorbing materials with reflectivity of T<-10 dB

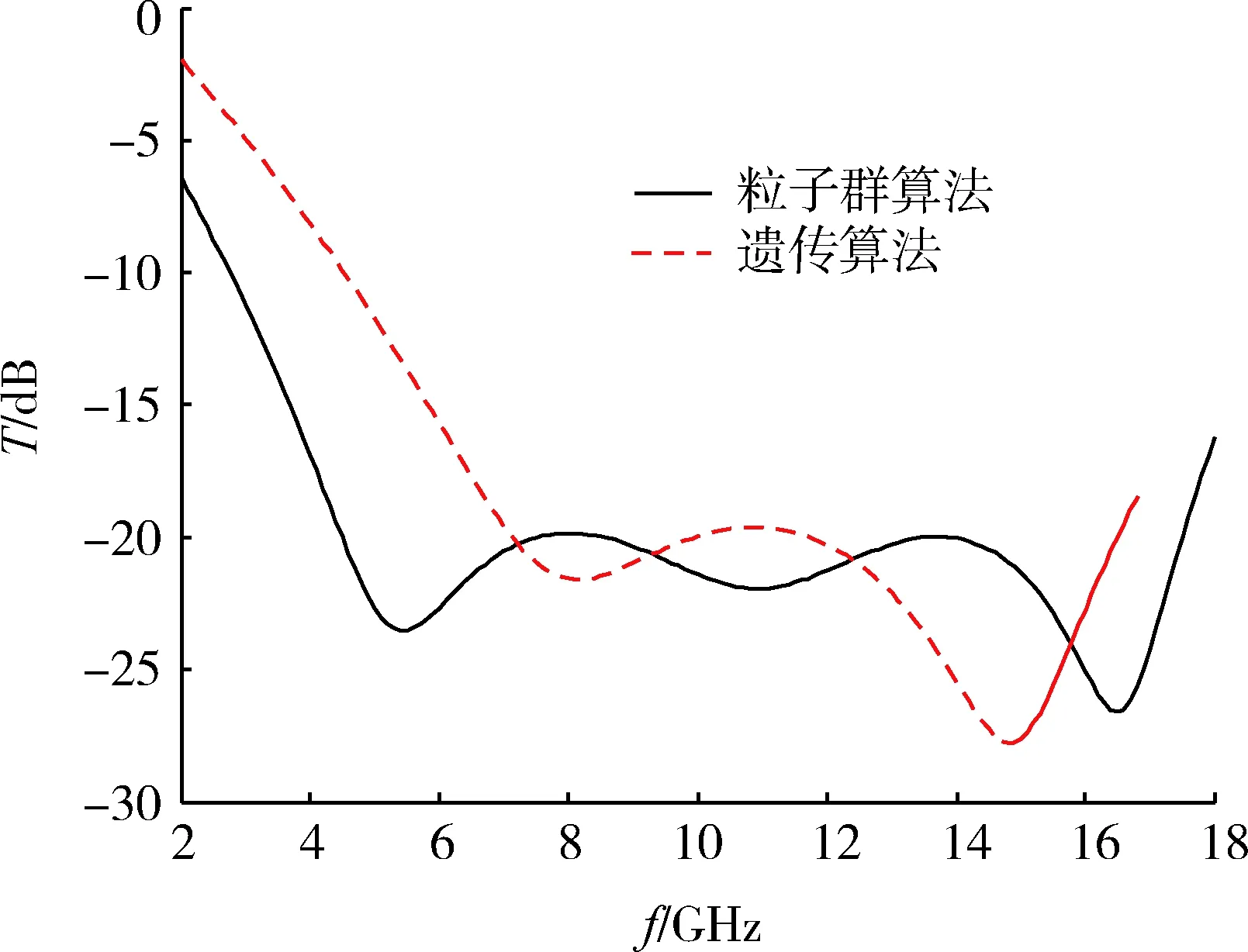
图8 三层吸波材料反射率T<-20 dB 2种优化算法分析Fig.8 Comparison of two optimization algorithms for three layers of absorbing materials with reflectivity of T<-20 dB

针对3层吸波结构材料隐身优化比较发现，在反射率T<-15 dB条件下，粒子群优化算法频率带宽约在3 GHz～17.5 dB，遗传算法频率带宽约在5～17 GHz范围内，并得到了相应算法的介电常数，隔离层厚度及电阻的值，如表1所示，发现了粒子群优化算法的反射率总和小于2 dB。结果表明，在同样优化条件下，采用粒子群优化算法能够得到较宽的频带，如图9所示。

表1 粒子群优化算法和遗传算法优化参数比较Table 1 Optimization parameters of PSO and Genetic algorithm

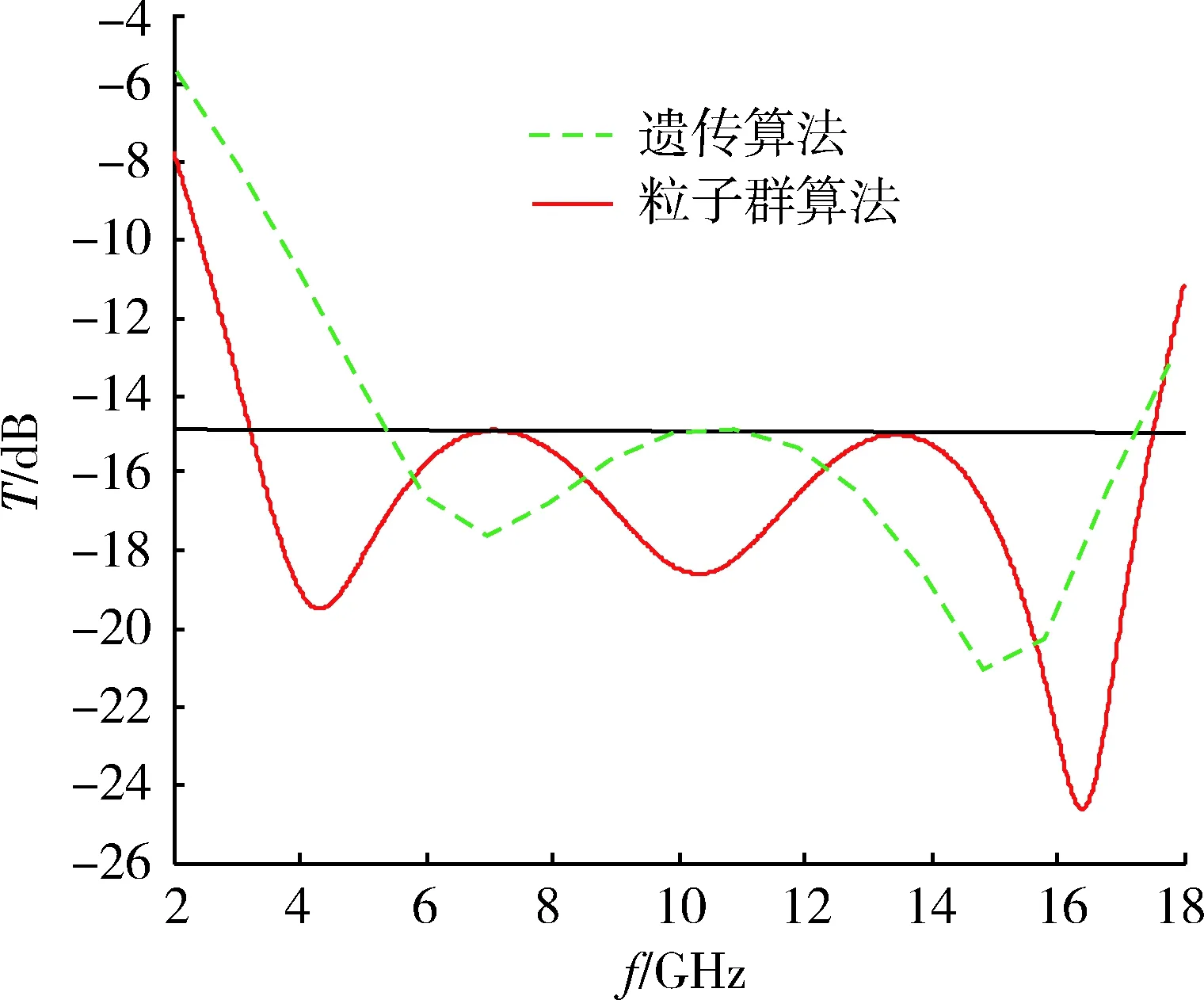
图9 反射率T<-15 dB条件下粒子群优化算法和 遗传算法频率带宽优化比较Fig.9 Comparison of frequency bandwidth optimization of particle swarm optimization algorithm and genetic algorithm with reflectivity of T<-15 dB

5 结束语

本文给出了采用粒子群优化算法针对吸波结构材料反射率频带的优化研究，比较了2种优化算法在不同反射率条件下的频带宽，发现了粒子群优化算法具有较宽的频带，并得出了以下结论：

首先，通过连续3次优化计算，在吸波材料反射率T<-15 dB条件下，发现遗传算法优化得到的反射率具有较大的区别，比较了2层吸波材料反射率T<-15 dB的频率带宽，粒子群优化算法比遗传算法频带宽约2 GHz，且得到了粒子群优化算法具有较好的稳定性。

其次，通过2种优化算法针对3层吸波材料反射率T<-10 dB和T<-20 dB进行优化比较，发现在2～8 GHz 2种算法反射率接近，整个频率范围内只有在2-15 dB；反射率T<-20 dB条件下2种优化算法频宽，在反射率相同的条件下，采用粒子群优化算法得到的频宽比遗传算法要大3 GHz，表明采用粒子群优化算法能得到较宽的频宽。

最后，在3层吸波材料反射率T<-15 dB约束条件下，对比了2种优化算法频宽，发现采用粒子群优化算法具有较宽的频带，并得到了该反射率条件下粒子群优化算法比遗传算法反射率总和要小2 dB。