运用交轨法探求轨迹方程问题

武增明

(云南省玉溪第一中学 653100)

如果一个动点是两条动曲线的交点，那么选取参数并把参数看成已知数，写出这两条动曲线的方程，再联立两动曲线的方程，消去参数，或者动曲线的方程与定曲线的方程联立，消去x或y，转化为一元二次方程，再消去参数，便得到动点的轨迹方程.这种求动点的轨迹方程的方法，我们称之为交轨法.运用交轨法探求轨迹方程问题，主要是把选取的参数看成已知数，写出两条动曲线方程，关键是参数的选取，困难是参数的消去.怎么把选取的参数看成已知数，写出两条动曲线方程？如何选取参数？怎样消去参数？在这里，笔者重点对如何选取参数及选取参数的思维途径有哪些作一些归纳、总结、探究，以飨读者.

一、选取动点(x0，y0)为参数

如果动点(x0，y0)影响动点P(x，y)的轨迹，起制约作用，那么就选取动点(x0，y0)为参数.

例1 已知圆O：x2+y2=4与x轴交于A，B两点，点M为圆O上异于A，B的任意一点，圆O在点M处的切线与圆O在点A，B处的切线分别交于点C，D，直线AD和BC交于点P，设P点的轨迹为曲线E，求曲线E的方程.

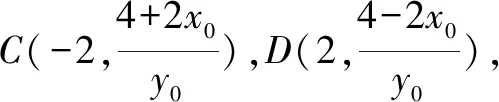
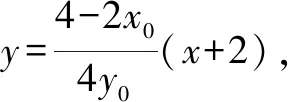
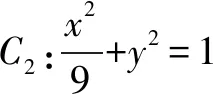
(1)当t为何值时，矩形ABCD的面积取得最大值？并求出其最大面积；

(2)求直线AA1与直线A2B交点M的轨迹方程.

解(1)设A(x0，y0)，则矩形ABCD的面积S=4|x0||y0|.

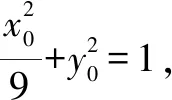
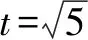
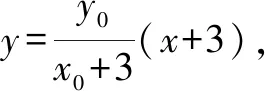
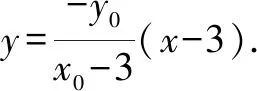
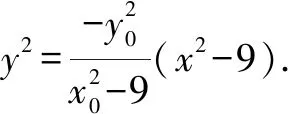
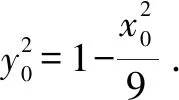
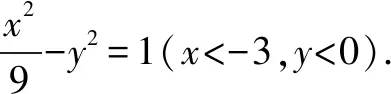
二、选取动直线的斜率k为参数

如果动直线的斜率k影响动点P(x，y)的轨迹，起制约作用，那么就选取动直线的斜率k为参数.

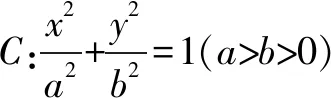
(1)求椭圆C的标准方程；

(2)若动点P(x0，y0)为椭圆C外一点，且点P到椭圆C的两条切线相互垂直，求点P的轨迹方程.

(2)设两切线为l1，l2，P(x0，y0).

(9k2+4)x2+18(y0-kx0)kx+9(y0-kx0)2-36=0，因为直线与椭圆相切，所以Δ=0，得

9(y0-kx0)2k2-(9k2+4)[(y0-kx0)2-4]=0，

∴ -36k2+4[(y0-kx0)2-4]=0，

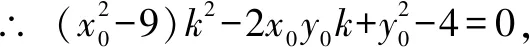
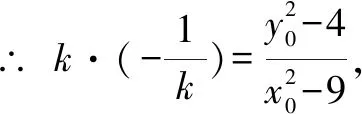
综上知，点P的轨迹方程为x2+y2=13.

评注本题第二问，抓住相切，则判别式等于零是关键.

三、选取动直线在y轴上的截距b为参数

如果动直线在y轴上的截距b影响动点M(x，y)的轨迹，起制约作用，那么就选取动直线在y轴上的截距b为参数.

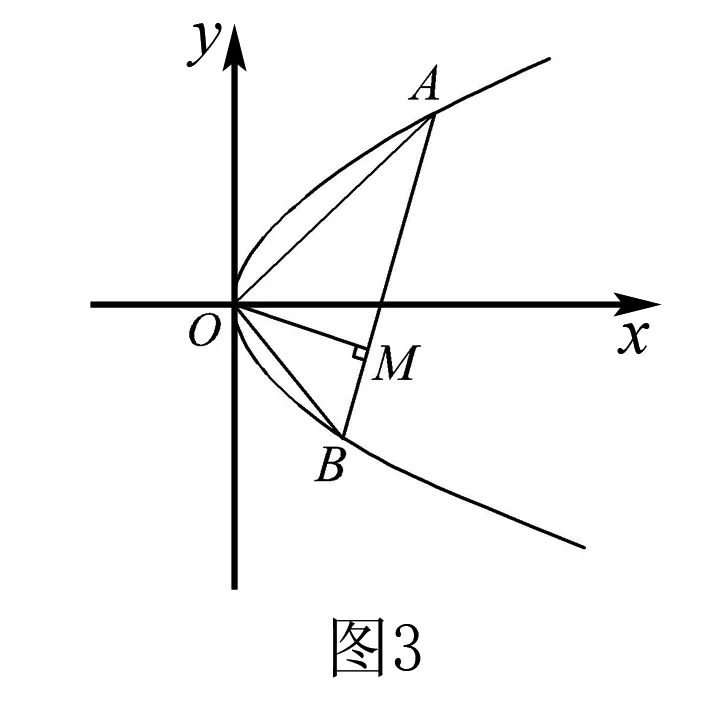
例4 (2000年高考春季招生考试北京，安徽卷·文23理22)如图3，设点A和B为抛物线y2=4px(p>0)上原点以外的两个动点，已知OA⊥OB，OM⊥AB.求点M的轨迹方程，并说明它表示什么曲线.

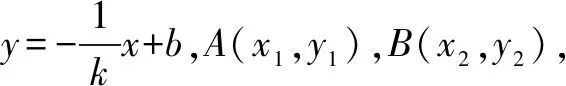
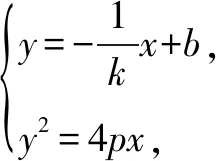
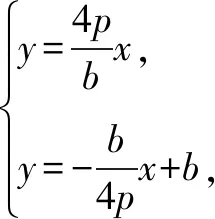
故点M的轨迹方程是(x-2p)2+y2=(2p)2(x≠0)，它表示以(2p，0)为圆心，2p为半径的圆，去掉原点.

评注找到k与b的关系式kb=4p后，直线OM的方程和直线AB的方程都可以用k来替换b，这样两直线方程联立，消去参数k，即得所求.

四、选取两线段之比λ为参数

如果两条线段之比λ影响动点P(x，y)的轨迹，起制约作用，那么就选取两条线段之比λ为参数.

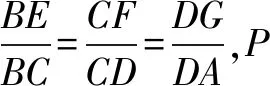
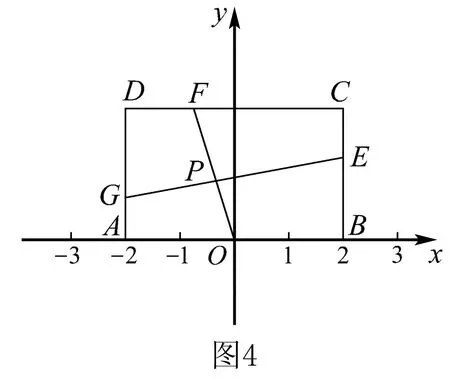
解由题意，得A(-2，0)，B(2，0)，C(2，4a)，D(-2，4a).

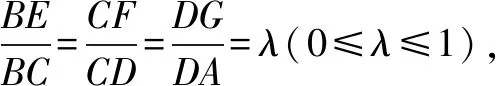
设P(x，y)，则有OP=(x，y)，OF=(2-4λ，4a)，GP=(x+2，y-4a+4aλ)，GE=(4，8aλ-4a)，由OP∥OF，得

4ax=y(2-4λ)， ①

GP∥GE，得

(x+2)(8aλ-4a)=4(y-4a+4aλ)， ②

由①②消去参数λ，得点P的坐标满足方程为2a2x2+y2-2ay=0.

所以点P的轨迹方程为2a2x2+y2-2ay=0.

五、选取动直线的倾斜角为参数

如果动直线的倾斜角α影响动点P(x，y)成迹，起制约作用，那么就选取动直线的倾斜角α为参数.

例6 定直线l与x轴的距离为a，交y轴于点N，设过原点O作一直线交l于点Q，在直线OQ上任取一点P，过点P作PM⊥x轴，垂足为M，且使|MP|=|NQ|，求P点的轨迹方程.

解因为a>0，所以为方便起见，设直线l在x轴上方，PM也在x轴上方，如图5.

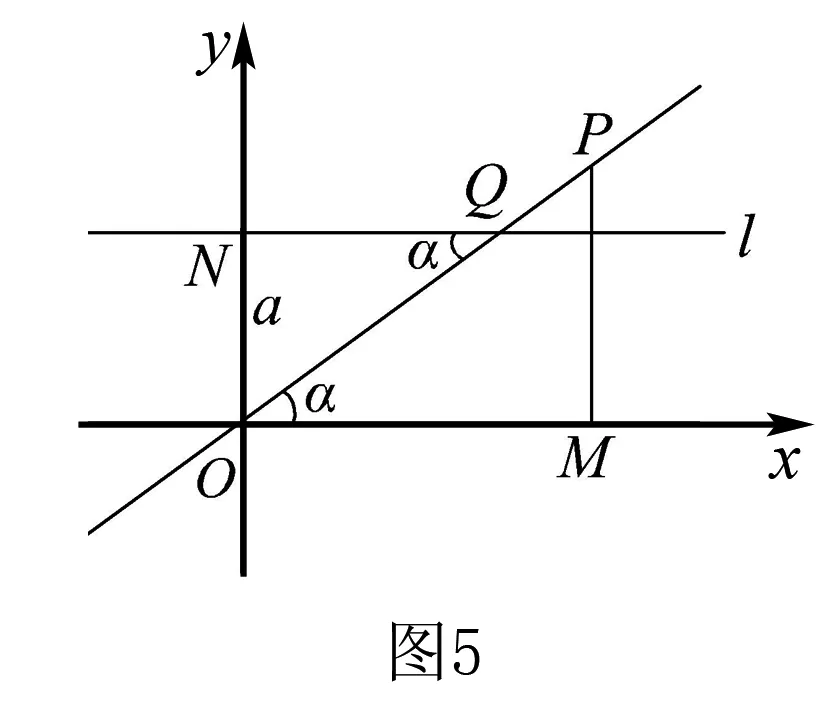
设直线OP的倾斜角为α，设P(x，y)，则

直线OP的方程为y=x·tanα. ①

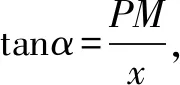
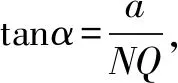
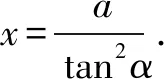
由①②联立消去参数α，得y2=ax.

直线l在x轴下方也符合题意.

故P点的轨迹方程为y2=ax.

运用交轨法探求轨迹方程问题，为什么要选取参数？通过解答上述例题，我们更进一步清楚，所求的曲线是两条动曲线的交点P(x，y)所形成的，既然是动曲线，所以这两条动曲线的方程一定含有参数.

如何选取参数？选取参数的思维途径有哪些？选取参数的依据是什么？通过解答上述例题，我们可以发现，应该选取影响动点成迹，起制约作用的那些关键量作为参数，如斜率、点、截距、长度、角度、两线段之比等，具体怎样选取参数，要根据题目所给条件，结合图形特点进行分析判断选取.