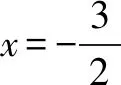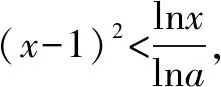高考和模拟题中的十类败题与错题
刘彦永
(吉林省长春市东北师范大学附属中学 130000)
类型一:题目不严谨
1.(2014年高考山东理6题)直线y=4x与曲线y=x3在第一象限内围成的封闭图形的面积为( ).
败因:因为第一象限内没有坐标原点,所以直线y=4x与曲线y=x3在第一象限内不可能围成封闭图形,将“第一象限内”改为“第一象限及其边界上”.
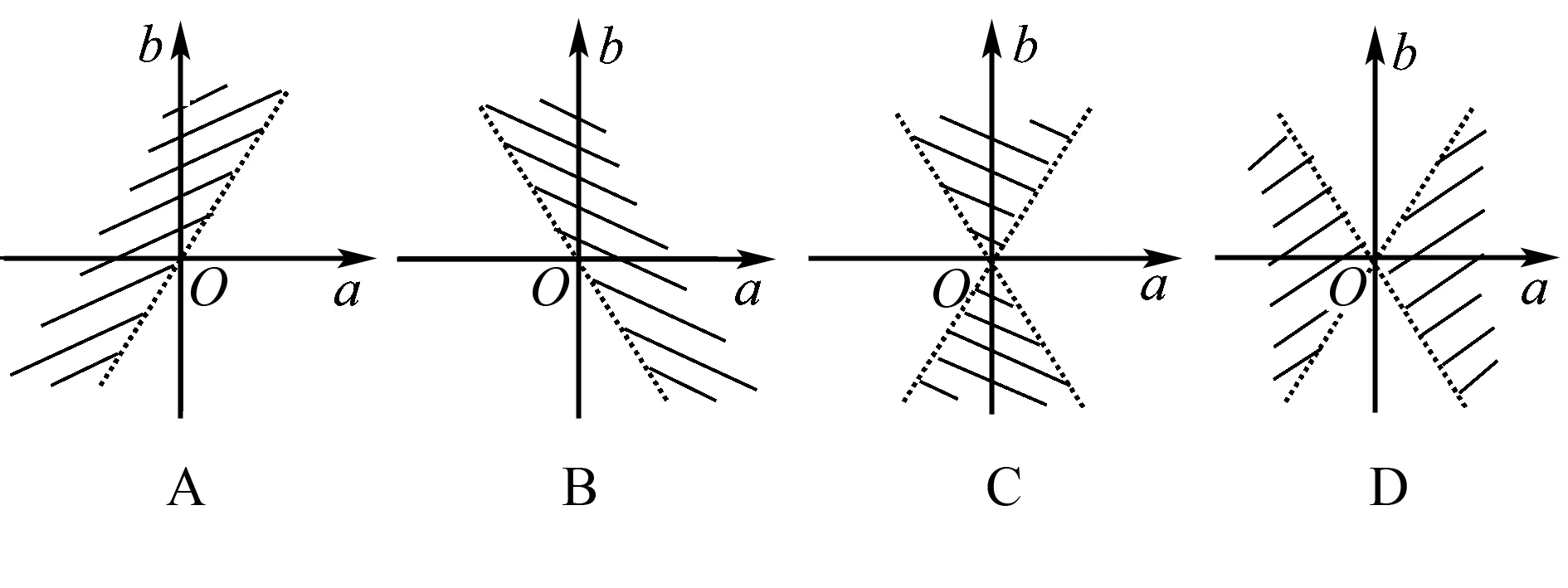
2.(2003年高考江苏1题)如果函数y=ax2+bx+a的图象与x轴有两个交点,则点(a,b)在aOb平面上的区域(不包含边界)为( ).
败因:本题标准答案给的是C,但由a≠0知对应图形中不包含b轴,应画为虚线.
点评以上两题属于败题,虽然不影响作答,但作为高考的权威性和引用的广泛性,还是要注意表述上的严谨.
类型二:用词不明确
3.(2017年高考北京理数8)根据有关资料,围棋状态空间复杂度的上限M约为3361而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与最接近的是(参考数据:lg3≈0.48)( ).
A.1033B.1053C.1073D.1093


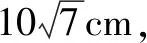
(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.
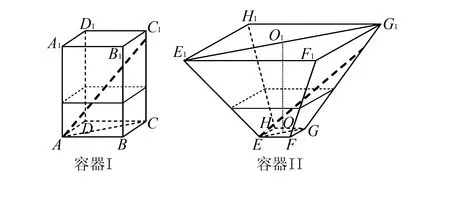
错因:“没入”既可以理解为入水,也可以理解为未入水,学生不同的理解就会得出不同的答案.
点评:命制试题时要注意用词不能引起歧义.
类型三:设问不适宜
5.已知函数f(x)=2ex-x3ex.
(1)求函数f(x)在(0,f(0))处的切线方程;


(2)若f(x)≤0,证明:a≤1-b.
败因:对于(2)问,因为f(x)≤0,所以f(1)=a-1+b≤0,直接得结论a≤1-b.
点评上述两题来自高三模拟试题,设问可以由条件直接快速得出,失去了压轴题考查学生能力和区分水平的功效,在试题命制中应反复斟酌,避免这类“乌龙”题.
类型四:定义不符合
7.若f(cosx)=sin2x,则f(sinx)=( ).
A.sinxB.-sin2xC.cosxD.-cos2x

点评不符合函数定义的这类题目在教辅资料里比较多见,对函数概念不清的学生造成了很大困扰.
类型五:结果不检验
8.(2013年高考浙江理15题)设F为抛物线C:y2=4x的焦点,过点P(-1,0)的直线l交抛物线C于A,B两点,点Q为线段AB的中点.若|FQ|=2,则直线l的斜率等于____.

点评在数学解题过程中,要注意变形的等价性,也要注意对结果的检验,尤其是出现答案多解的情况更要提高警惕.
类型六:“模型”不存在
9.一个等比数列{an}共有2n+1项,奇数项之积为100,偶数项之积为120,则an+1为.
错因一方面,由a1a3…a2n+1=100,a2a4…a2n=120作商有

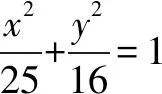

点评这类错题可谓“深藏不露”,若不深入探究不知“错”在哪里,还会自以为“是”,因此是流传更为广泛的一类错题.
类型七:“模型”不唯一
11.(2010年福建高考理12题)若一个底面是正三角形的三棱柱的正视图如图1所示,则其表面积等于.

错因标准答案是按照图2给出,事实上,根据条件得到的三棱柱可能是图3(调整角度后的图,便于读者理解),即侧棱未必与底面垂直,这样本题的答案就不确定了.
点评这类错题产生的原因就是条件过于“开放”,导致模型不唯一,此类错题多出现在立体几何试题中,如,给定的三视图对应的几何体未必是唯一的.
类型八:条件不相容
12.已知定义在R上的奇函数f(x)满足条件f(x+2)=-f(x),当-2 A.-1 B.0 C.2017 D.2018 事实上,定义在R上的奇函数f(x)满足则f(x+2)=-f(x),则也有f(-x-2)=f(x),即函数的图象关于直线x=-1对称,与-2 点评题目的已知条件制约关系太多,若充分挖掘就会发现自相矛盾,这也是一类流传较多的错题,值得关注. 类型九:答案不正确 13.(2005年福建理12题)若f(x)是定义在R上的以3为周期的奇函数,且f(2)=0,在区间(0,6)内f(x)=0的解的个数的最小值是( ). A.3 B.4 C.5 D.6 错因本题标准答案给的是C,根据条件容易知道f(1)=f(2)=f(3)=f(4)=f(5)=0,忽略了f(1.5)=f(4.5)=0,故正确答案应该是7. 类型十:试题不可解 14.不等式(x-1)2 点评可以将本题改编为“不等式(x-1)2>logax对x∈(0,1)恒成立,求实数a的取值范围.”遇到错题时可以适当交给学生探究和讨论,培养学生发现问题和解决问题的能力. 美国著名数学教育家波利亚说过,掌握数学就意味着学会解题,而想要学会解题,好的数学题目是关键.我们急需深刻总结和反思命制好题的经验,更要汲取错题命制的教训,力争命制出高质量的好题.