用三面角余弦定理巧解二面角问题
李昌成
(新疆乌鲁木齐市第八中学 830002)
现在立体几何中引入了空间向量,解决二面角问题学生首选向量法,但是往往因为建系不准确,运算出差错造成失分.由于过于依赖空间向量,对于传统的办法更是望而生畏.下面介绍一种既不建系,也不过多依靠空间位置的方法,用以解决二面角问题.
一、认识定理
1.三面角的定义
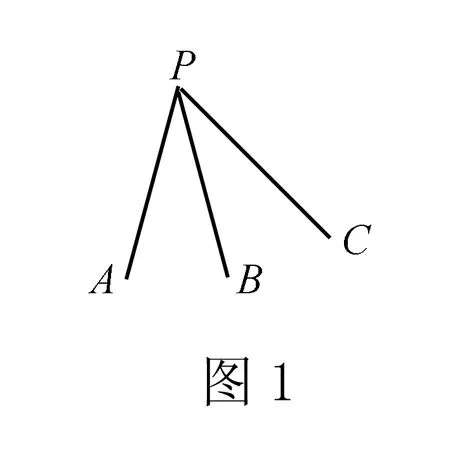
由空间中一点P引三条不共面的三条射线PA,PB,PC,以及相邻两射线间的平面部分所构成的几何图形叫做三面角.记作:三面角P-ABC,P叫做顶点,PA,PB,PC,叫三面角的棱.∠BPC,∠CPA,∠APB叫三面角的三个面角.C-PA-B,A-PB-C,B-PC-A叫三面角的三个二面角(如图1).
2.三面角余弦定理
如图1,若三面角的三个面角分别为α,β,γ,它们所对的二面角分别为C-PA-B=A,A-PB-C=B,B-PC-A=C,则
cosα=cosβcosγ+sinβsinγcosA;
cosβ=cosγcosα+sinγsinαcosB;
cosγ=cosαcosβ+sinαsinβcosC.(证明略,有兴趣的老师可以证一下)
3.本质分析
从三面角余弦定理的结构可以发现,每个公式仅含有某个二面角和三个面角.从方程的角度考虑,要求某个二面角,只需求三个面角的正余弦.进而转化成平面上解斜三角形问题,将空间问题平面化,体现了转化思想,同时规避了找二面角的困难以及向量法的繁杂运算.例如,在正四面体中,三个面角α=β=γ=60°,任意两个面所成的二面角φ均满足:
cos60°=cos60°cos60°+sin60°sin60°cosφ,
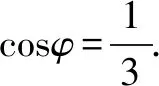
二、应用定理
1.求三棱锥中的二面角
三面角存在于三棱锥之中,因此三面角余弦定理解决三棱锥中的问题,包括求面角和二面角都应该是最得心应手的,我们来研究一道这方面的高考题.
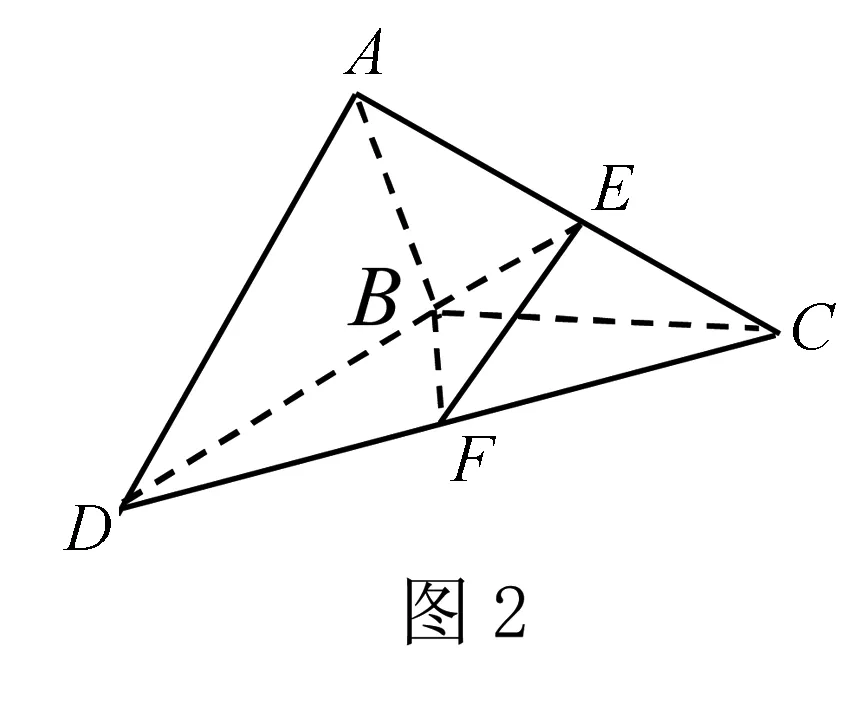
例1 (2014年高考数学辽宁卷理科第19题)如图2,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别是AC,DC的中点.
(1)求证:EF⊥BC;
(2)求二面角E-BF-C的正弦值.
解(1)略.(2)在三面角B-ACD中,cos∠ABD=cos∠ABCcos∠DBC+sin∠ABCsin∠DBCcos90°
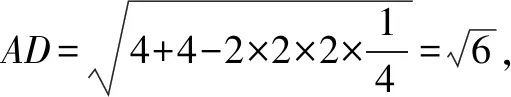
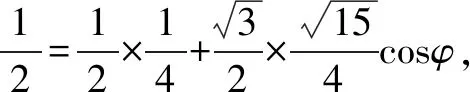
评注本题两次使用三面角余弦定理,第一次用于求面角,第二次用于求二面角.完全避开了两次找二面角的风险,也没有向量法的大量运算.△ABC和△BCD所在平面互相垂直,即二面角A-BC-D的大小为90°,学生容易错误地认为∠ABD=90°,必然导致AD的值错误,也可能导致建立错误的空间直角坐标系,最终都是计算出错误的二面角E-BF-C的正弦值.最可悲的是,在解答过程中这种错误学生没有感觉.大家可以尝试用其他方法解答,然后对比,喜悦之情,油然而生.
2.求非三棱锥中的二面角
三面角余弦定理本质上与三棱锥紧密结合,给人的感觉是似乎在非三棱锥中就无用武之地.实际上在非三棱锥中构造出三棱锥,三面角余弦定理依然可以正常使用.下面再研究一道高考题.
例2(2017年高考数学全国Ⅰ卷理科第18题)如图3,四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
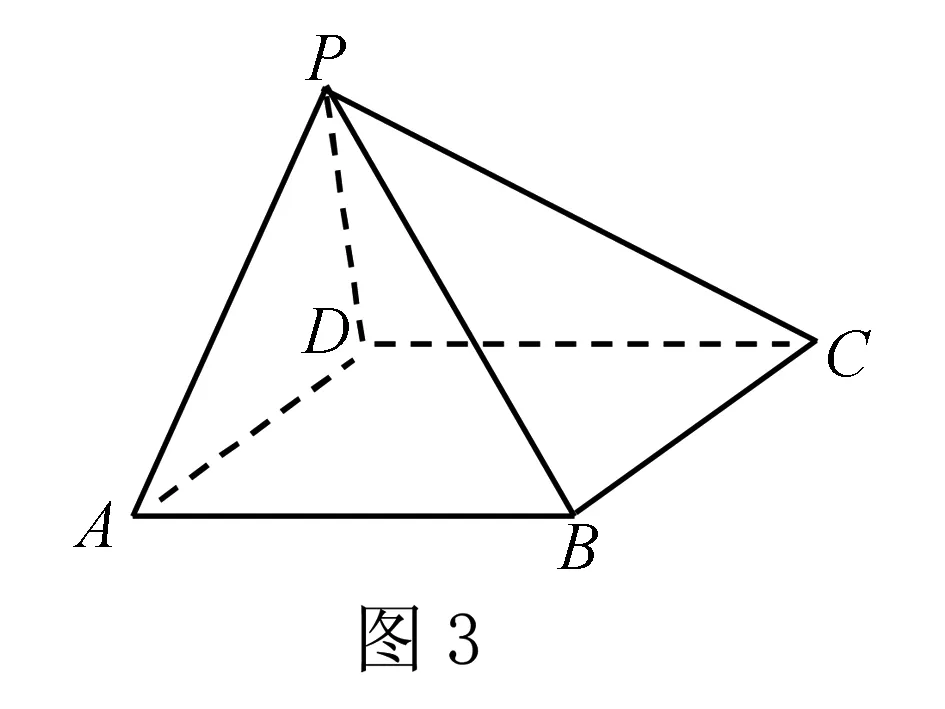
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.
解(1)略.
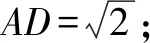
评注解答中巧妙构造了三面角B-APC,问题变得一目了然,要求二面角A-PB-C,只需要求三个面角∠ABP,∠PBC,∠ABC,进而求各条棱棱长.本题中的所有棱长都直接或间接地给出了,条件显得十分饱满,非常合适使用三面角余弦定理解答.相对于当下流行的向量法,整个计算过程十分轻松愉悦.不失为一个好办法.
3.证明面面垂直
面面垂直的定义是:两个平面相交,它们所成的二面角是直二面角,就说这两个平面互相垂直.依此定义,只要计算出二面角为直角就可证明面面垂直!那么,三面角余弦定理是可派上用场的!
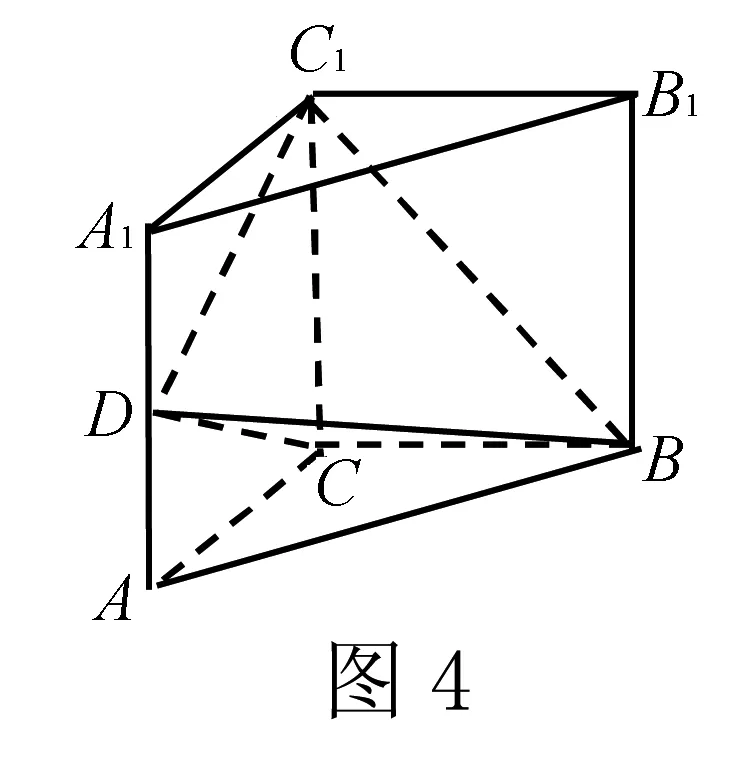
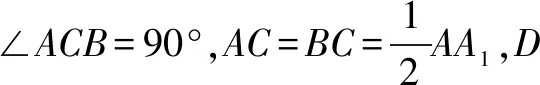
(1)证明:平面BDC1⊥平面BDC;(2)略.
证明(1)设AA1=2,则AC=BC=1,

令二面角C-BD-C1的平面角为φ,在三面角D-BCC1中,cos∠CDC1=cos∠BDC1cos∠BDC+sin∠BDC1sin∠BDCcosφ,易解得cosφ=0,φ=90°,所以平面BDC1⊥平面BDC.
评注对于空间想象能力不太强的文科生来说,这种解法可以使他们从难以想象的位置关系中解脱出来.通过不算复杂的运算(主要是平面内勾股数组运算)求出面角,进而求出二面角,最后得出位置关系结论.
三、链接练习
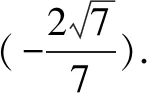
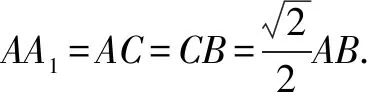
对于一种新方法,我们总有一个认识的过程.第一感觉是陌生,排斥它;然后慢慢地接触它,逐渐熟悉它;然后有意应用它,体会其优越性;最后真正地爱上它.三面角余弦定理本身形式较为复杂,容易被人抛弃,但是只要掌握了,它的应用还是很方便的.只要几何体中的线条数量关系明确,不管位置关系多么隐蔽,都能准确快捷求得相关的面角和二面角以及证明面面垂直.三面角余弦定理最大的功能是:空间问题平面化.对于空间想象能力弱一点的学生来说,毫无疑问是最大的福音.

