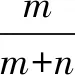建构“糖水浓度”模型速解一类题

钟建新

(浙江省绍兴市春晖中学 312300)

题目1 (2018年5月诸暨高考模拟试题9) 甲盒子装有3个红球，1个黄球，乙盒中装有1个红球，3个黄球，同时从甲、乙两盒子中取出i(i=1,2,3)个球交换，分别记甲、乙两个盒子中红球个数的数学期望为E1(i),E2(i)，则以下结论错误的是( ).

A.E1(1)>E2(1) B.E1(2)=E2(2)

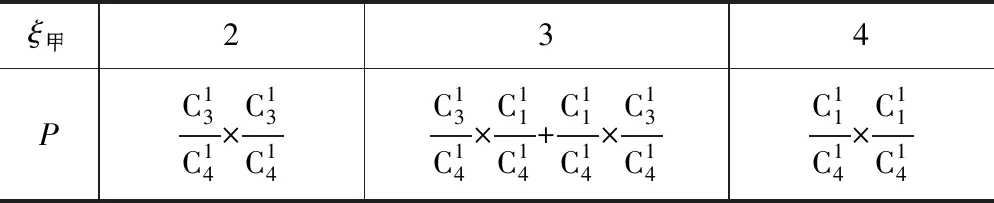
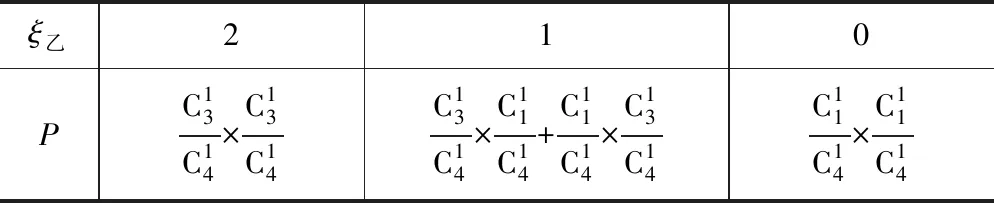
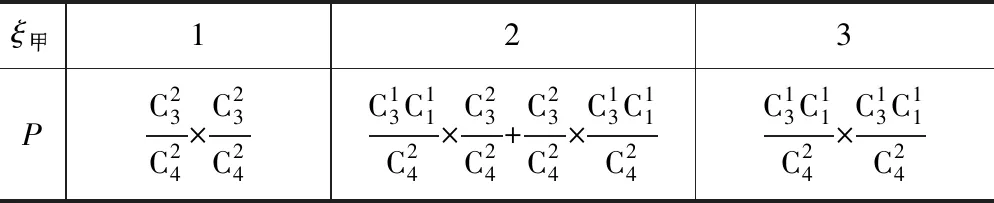
C.E1(1)+E2(1)=4 D.E1(3)

分析当i=1时，

ξ甲234PC13C14×C13C14C13C14×C11C14+C11C14×C13C14C11C14×C11C14

ξ乙210PC13C14×C13C14C13C14×C11C14+C11C14×C13C14C11C14×C11C14

又当i=2时，

ξ甲123 PC23C24×C23C24C13C11C24×C23C24+C23C24×C13C11C24C13C11C24×C13C11C24

ξ乙321PC23C24×C23C24C13C11C24×C23C24+C23C24×C13C11C24C13C11C24×C13C11C24

∴E1(2)=2,E2(2)=2，∴E1(2)=E2(2).∴选D.

上述解法虽可用，但对于求解此题过程略显繁杂，下面提供一种简单分析思路.

可建构“糖水浓度”的模型解释，把红球对应看成糖，黄球对应看成水，则甲盒子原先的糖水浓度为75%，乙盒子原先的糖水浓度为25%，可见交换球的次数越多，甲盒子的糖水浓度会越来越淡，相反乙盒子的糖水浓度会越来越浓.在交换各自总质量(此题中甲、乙两盒的总质量相等)的一半时，即交换2个球，甲、乙两盒的糖水浓度相等，均为50%；交换1个球，糖水浓度仍是甲盒的高；交换3个球，糖水浓度则是乙盒的高;交换4个球，甲盒子的糖水浓度为25%，乙盒子的糖水浓度为75%.但无论是交换1个球，2个球，3个球，还是4个球，甲、乙两盒中的红球的总个数是一样的，即4个.

题目2 (2018年5月杭州二中高三仿真考题9)已知甲盒子中有m个红球，n个蓝球，乙盒子中有m-1个红球，n+1个蓝球(m≥3,n≥3)，同时从甲、乙两个盒子中取出i(i=1,2)个球进行交换，(a)交换后，从甲盒子中取1个球是红球的概率记为pi(i=1,2).(b)交换后，乙盒子中含有红球的个数记为ξi(i=1,2).则( ).

A.p1>p2,E(ξ1)

B.p1E(ξ2)

C.p1>p2,E(ξ1)>E(ξ2)

D.p1

感悟建构“糖水浓度”模型求解取球并交换涉及到的概率、期望大小判定等有关问题，可以由表及里，抓住事物的本质，快速找到事物间内在的联系，其中所蕴含着的数学思想和方法可谓精彩纷呈，妙趣横生！