贵阳市南明河气动盾形闸门结构自振特性分析

何 伟，武 芳

（1.贵州省水利水电勘测设计研究院，贵州 贵阳 550002；2.湖北拓普电力有限公司，湖北 武汉 430000）

0 引言

贵阳市南明河气动盾形闸门规格为60m×8m（宽×高），门顶溢流最大水深为0.205 m，最大挡水头为8.205 m，于2013年12月竣工投入运行使用，目前运行情况良好。该气动盾形闸门规模创世界纪录协会世界最高的气动盾形闸门纪录，是目前挡水最高的气动盾形闸门，因此有必要对闸门的自振特性进行分析，得到气动盾形闸门的各阶自振频率和振型模态，进行初步的共振校核，为气动盾形闸门的设计及安全提供依据和参考价值。

根据气动盾形闸门的运行条件，闸门振动的产生有外因和内因，其中外因主要有边界水流条件、闸门的开度、安装时施工的缺陷、水位变化及操作运用等；内因主要是本身的结构，如面板、支撑气囊、顶缘结构、面板肋板、埋件及其他零件的磨损。气动盾形闸门的自振是闸门振动的内因，闸门自振频率是结构本身的固有参数，决定于闸门结构的刚度、质量分布和材料性质等[1]。本文主要研究气动盾形闸门在上游水荷载和相应约束条件下，采用有限元法进行闸门自振振动特性分析，主要思想是将闸门各主要部件分别用有限元离散，按单个构件进行分析[1]。强迫振动振源水流与气囊未直接接触，是否产生共振还取决于振源的能量和传播路径，需要进一步进行闸门动力响应分析，本文不予研究。

1 闸门有限元模型建立

由于气动盾形闸门在垂直水流方向具有对称性，根据结构力学对称结构的求解原理，本文有限元分析仅取单节门体进行分析计算。单节门体宽度10 m为一个结构单元，采用在ANSYS中直接建模的方法，气动盾形闸门细部结构复杂，通过焊接及装配得到空间装配式结构，在建立气动盾形闸门有限元模型时不可能全部考虑这些复杂的细部构造[2]，否则有限元模型过于复杂难以用于分析计算。在建立气动盾形闸门有限元模型时，需要进行简化。气囊内部表面节点施加均布荷载模拟气囊内压。计算模型采用笛卡尔直角坐标系，X轴为水平方向，指向下游为正；Y轴为铅直方向，向上为正；Z轴为垂直水流方向，指向右侧（面向下游）为正；其中，坐标系原点取在闸门的底轴轴心处。设计参数采用肋板和面板四节点壳单元模拟，抑制带采用二节点梁单元模拟，其余采用八节点实体等参单元模拟。有限网格划分结果及材料参数见表1。

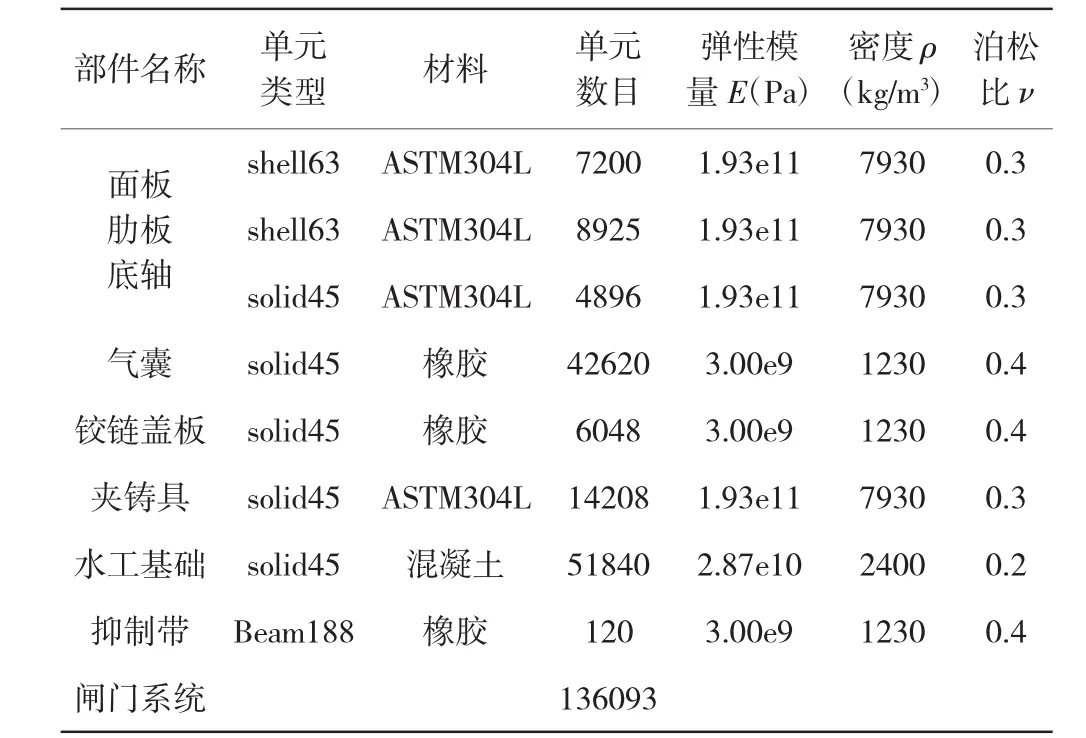
表1 各部件设计参数

对于闸门水体质量采用六自由度质量单元MASS21模拟作用在闸门迎水面，各结构部位质量单元的实常数通过实际荷载与单元节点数计算得到。闸门有限元三维模型见图1，闸门结构网格见图2。

图1 闸门有限元三维模型

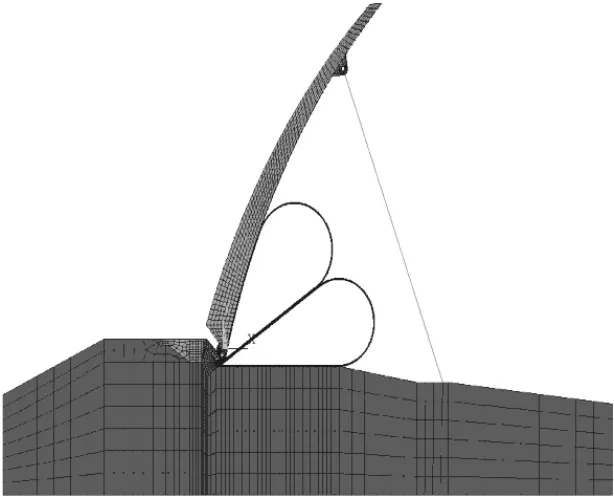
图2 闸门结构网格

2 闸门计算工况及有限元模型约束施加

气动盾形闸门是主要是承受上游水压力的作用，要求气动盾形闸门具有足够的强度和刚度来承受上游荷载。为了研究气动盾形闸门在上游水头作用下自振特性分析，本文主要分析气动盾形闸门在挡正常蓄水位8 m（工况1）和挡最大水头8.205 m（工况2），其下游水头均为0 m，气囊内压均为0.305 MPa下两种典型工况下的自振频率特性，气动盾形闸门大多数情况处于这两种工况下运行，其运行较频繁，时间较长，对气动盾形闸门的设计具有实际指导意义。

约束施加计算中主要涉及如下4种约束：

（1）气动盾形闸门水工基础为离散刚体，其底部为全约束；基础上下游断面边界施加水流方向约束（即坐标轴x方向）；基础横河向截断面边界施加垂直于水流方向约束（即坐标轴z方向）。

（2）抑制带与门体上安装孔采用耦合约束。气囊与闸门面板之间采用摩擦方程约束。在门体与气囊采用建立接触，接触类型为表面与表面接触，接触属性定义为切向行为，根据《现代机械设计手册》表1-1-7中常用材料的摩擦因数，设定摩擦系数为0.8。

（3）上气囊与下气囊、下气囊与水工基础、铰链盖板之间连接部分位移较小，假定不产生相对位移，模型采用假定以上部位单元均共节点。

（4）由于气囊和抑制带的刚度相对闸门结构较小，为避开气囊和抑制带的振型，进一步了解闸门结构的自振特性，只考虑气囊的支撑作用，下游气囊单元为全约束，模型不包含抑制带（杀死抑制带），且基础假定为弹性地基。

根据上述闸门模型进行加载，施加约束，进行模态分析并拓展模态，得出闸门在不同振阶下的频率[4]。求解并分析气动盾形闸门这两种工况下的自振频率特性。

3 闸门自振特性分析

在模态计算中，采用分块Lanczos迭代法提取了前50阶模态。对闸门结构进行了上述两种工况的计算，根据计算结果，将前50阶中具有代表性的模态图列于表2，将2种工况闸门结构前50阶的自振频率和相应模态特征加以整理列于表3。

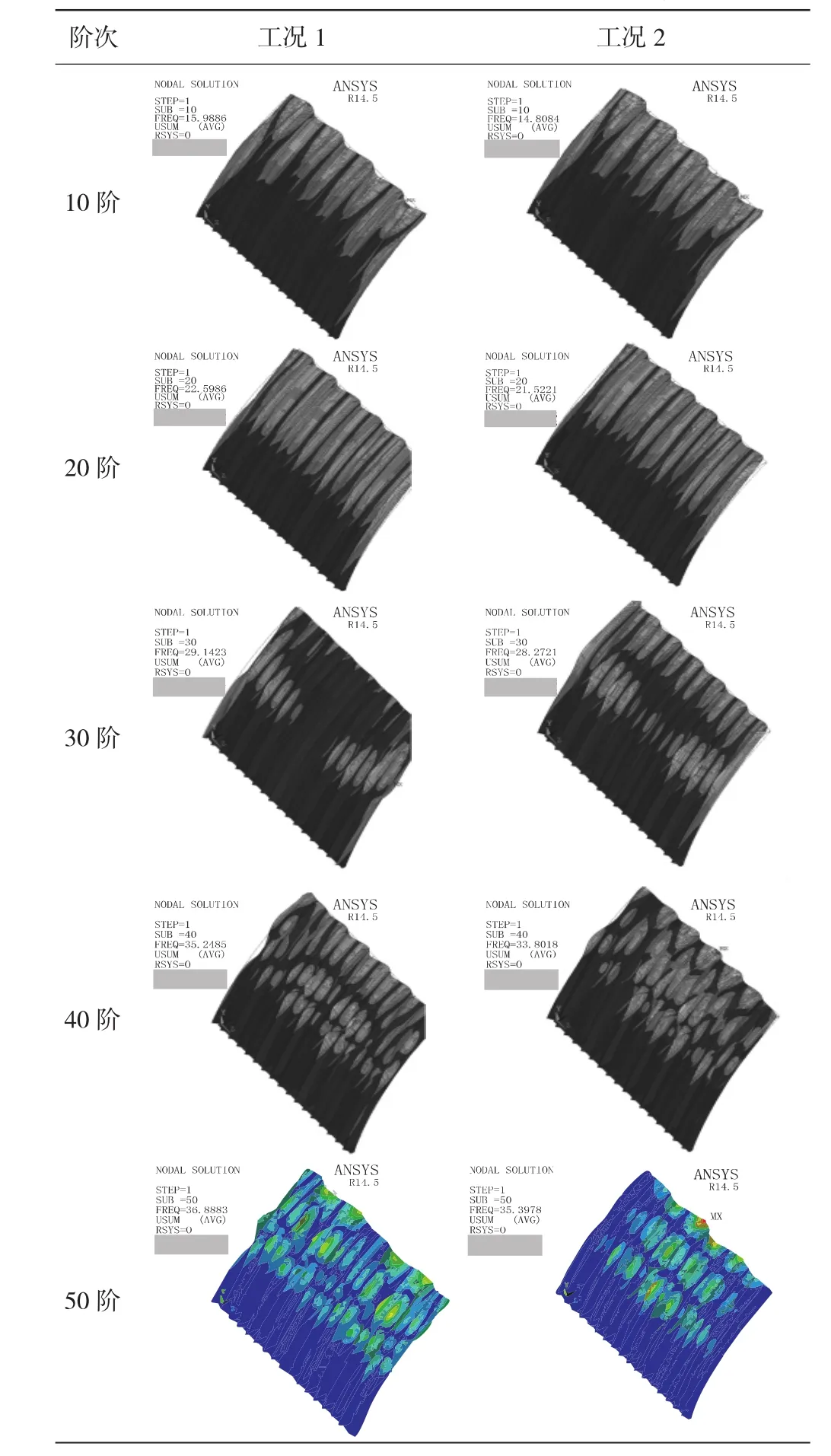
表2 闸门结构自振频率与模态云图统计表

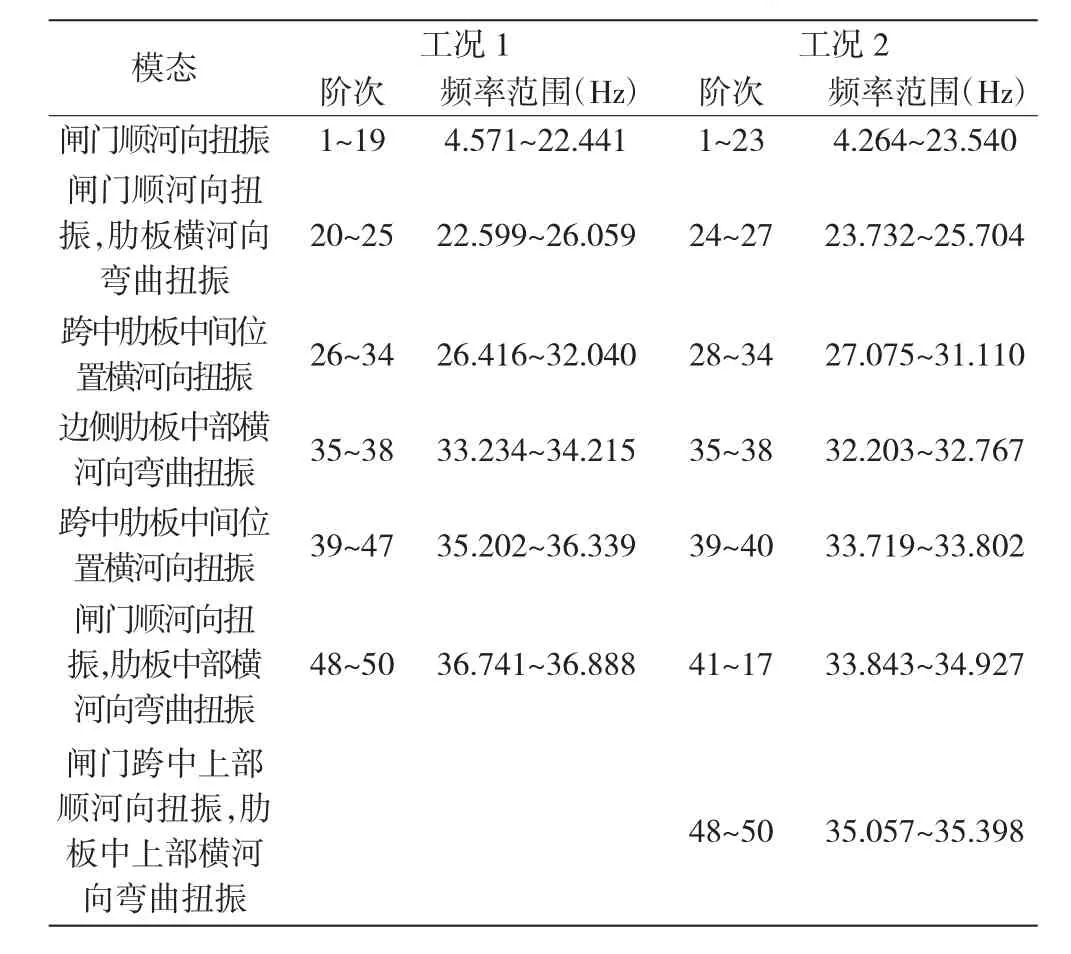
表3 闸门结构自振频率与模态统计表

4 闸门两种工况自振特性分析及对比

（1）由表2和表3可知，工况1上游挡水高度8.0 m时，闸门的前19阶，均为钢闸门顺河向的振动；从第20阶（频率22.59 Hz）模态开始，肋板开始横河向振动，此阶段闸门顶部和肋板同时振动。从第35阶（频率33.23 Hz）模态开始，两侧面板顺河向扭振，同时边侧肋板横河向扭振，此振型的出现初步判定和两侧不存在气囊的支撑作用有关。从第39阶（频率35.20 Hz）模态开始，面板中上部和肋板中上部同时振动。

（2）由表2和表3可知，工况2上游挡水高度8.205 m时，闸门的前23阶，均为闸门顺河向的振动；从第24阶（频率23.73 Hz）模态开始，肋板开始横河向振动，此阶段闸门顶部和肋板同时振动，此振型较工况1晚出现。从第35阶（频率32.203 Hz）模态开始，两侧面板顺河向扭振，同时边侧肋板横河向扭振，与工况1类似，这是因为该部位不存在气囊的支撑作用。从第39阶（频率57.98 Hz）模态开始，面板中上部和肋板中上部同时振动。

（3）考虑水体对闸门的耦合影响后，气动盾形闸门的自振频率有所降低，降低幅度随挡水高度的增大而增大。挡水高度为8.0 m时，考虑到上游水荷载的耦合作用影响使得一阶自振频率由11.71 Hz降至4.57 Hz，降幅为60.96%；而挡水高度为8.205 m时，一阶自振频率由11.71 Hz降至4.24 Hz，降幅为63.78%，降幅更大。

（4）两种工况一阶振型均为闸门顺河向扭振，二阶振型均为闸门顺河向振动。

（5）工况1第3～19阶、工况2第3～23阶的振型均为闸门顺河向扭振，主要为面板的扭振；工况1第19阶、工况2第23阶之后的振型，肋板的振动幅度逐渐增大，闸门的振型较为复杂。

5 结语

影响气动盾形闸门振动的原因繁杂，主要是强迫振动振源是水流脉动，但由于本工程未进行模型试验和原型观测工作，未取得水流脉动的激振频率。但参考《水电站机电设计手册》金属结构（一）中对国内外工程的15个模型试验资料和14个原型观测资料获得的水流的激振主频率数值来看，有93%的闸门，其水流的激振主频率在1 Hz～20 Hz氛围内，有48.3%的闸门在1 Hz～10 Hz范围之内，并且与水头和开度的变化关系不大[5]，因此，大于20 Hz的仅为极少数，可以认为水流的激振主频率为 1 Hz～20 Hz。

根据表2和表3自振特性分析及对比，可以得出以下基本结论：

（1）上游正常蓄水位即挡水高度为8.0 m时，闸门结构前17个阶次自振频率与水流脉动频率（1 Hz～20 Hz）有重合的可能性比较大，此工况下有可能发生共振；上游最高溢流水位即挡水高度为8.205 m时，闸门结构前18个阶次自振频率与水流脉动频率（1 Hz～20 Hz）有重合的可能性比较大，此工况下有可能发生共振。其他阶次，结构的大部分自振频率均大于20 Hz，发生共振的概率并不大。

（2）通过振型图可知，闸门的低阶振型主要为面板顶部的振动，而低阶振动又是振动分析的重点，所以设计过程中要注意提高闸门顶部的刚度。

（3）本工程中，低阶振动主要为面板的振动，且主要为面板顶部的振动，因此本工程中，顶部面板属于刚度较薄弱部位，是闸门结构抗振的重点处理部位。挡水高度越高，肋板结构较晚出现自振。

（4）总体来说，考虑水体对闸门的影响后，闸门自振频率有所降低，降低幅度随闸门挡水高度的增大而增大。因此，在闸门自振频率计算过程中不可忽视闸门与水体的耦合作用。