指向学生核心素养培育的高中数学集合单元教学研究

◎ 黄根初

《普通高中数学课程标准（2017年版）》指出，数学学科核心素养是数学学科育人价值的集中体现，也是数学课程目标的集中体现。实践表明，只有当数学学科核心素养目标与数学具体内容的教学结合在一起时，核心素养目标才能真正落到实处，也只有当具体内容的教学体现其独特的育人价值时，数学教学才是有力的。本文以集合单元为例，探索如何有机结合集合单元的教学与学科核心素养的培育。

一、 集合单元的育人价值

（一）集合思想是作为教育任务的一种全域性数学思想

集合论是现代数学重要而基本的理论，它的概念和方法已经渗透到数学的各个分支以及其他一些自然学科中，为这些学科的发展提供了奠基性的方法，改变了这些学科的面貌。

集合论的主要思想表现在：初等集合论思想、实无穷与超穷思想、集合对应思想。其中，在初等集合论思想指导下，我们可以把一类研究对象作为一个整体进行研究，依据概括原则可以构造一个集合，依据外延原则保证集合的确定性；集合对应思想反映了两个集合元素之间的关系。这些思想蕴含在教材集合单元的有关知识内容之中，如集合的运算中蕴含着运用求交集方法解决问题的思想，数学教育家波利亚（Polya）将其提炼为解决问题的“交轨模式”。

（二）集合语言是现代数学的基本语言

集合语言是现代数学语言的重要组成部分。数学语言和自然语言的重要区别在于数学语言更加精确，不容易产生歧义。在基础教育阶段学习使用集合的语言，可以准确、简洁地表示所要研究的对象，更好地描述研究对象之间的关系。

我们可以把各种几何图形看成是一个点集，然后研究它所包含的点在位置及数量关系方面的共同特征，这样往往能够得到比直观更为深刻的结论。例如，平面内线段AB的垂直平分线可以简洁地表示成点集{P│PA=PB}，它揭示了这样的本质：线段垂直平分线上的点到该线段两个端点的距离相等，到线段两个端点的距离相等的点在该线段的垂直平分线上。又如，我们可以利用集合语言刻画四边形及其特例的关系：{四边形}{平行四边形}{矩形}{正方形}。

（三）集合语言具有独特的育人价值

集合语言的独特育人价值表现在：用集合语言简洁、准确和深刻地表达数学内容的过程，可以很好地发展数学抽象等素养。数学抽象主要包括从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，并用数学语言予以表征。集合语言的学习体现了数学抽象过程的主要特征：集合的含义是在学生学习积累了大量集合例证的基础上概括出来的，在获得集合含义后就有必要用数学语言表征这个数学研究对象，进而研究集合之间的关系，最后研究集合的应用。

集合的育人价值还体现在可以展示学习研究数学的一种路径或方式：通过观察抽象归纳辨析等获得集合（数学研究对象）—研究集合的表示—类比实数之间的关系研究集合之间的关系—类比实数的运算研究集合的运算—集合的应用。通过这一方式，帮助学生使用集合的语言简洁、准确地表述数学研究对象，学会用数学语言表达和交流，体会用集合语言表达数学内容的优点，积累数学抽象的经验，发展数学抽象、数学运算、逻辑推理和直观想象等数学学科核心素养。

二、在集合单元的教学中发展学生的核心素养

不同版本的高中数学教材都有集合初步单元，它们都呈现了“集合的含义—集合表示—集合之间关系—集合运算”等知识内容结构，这一结构较好地反映了课程标准中关于集合单元的内容要求，为实现集合单元的育人价值提供了载体。 如何在集合单元的教学中发展学生数学学科核心素养，需要依托以下三个过程。

（一）依托集合的概念理解与表示过程

集合的概念是通过概括实例形成的。我们可以借助实例，分析这些实例中各自的研究对象。如果发现研究对象都满足一定要求或具有一定特征，则把研究对象的总体称为集合，集合中的对象称为元素。

上述过程是理解集合含义不可或缺的过程，其中实例要丰富和典型，它是理解集合含义的素材。这些实例既要包括学生在小学和初中接触过的一些数学的例子，如自然数、有理数的集合，不等式x-2＜3的解的集合，到一个定点的距离等于定长的点的集合；又要包括现实生活中的例子，如学校于2019年9月入学的所有高一学生；还要包括科学情境的例子，如我国从1970年到2018年发射的所有人造卫星等。丰富而典型的实例，既可以帮助学生打开视野，又可以帮助学生辨析、理解概念含义，领会其中的概括原则。

理解集合的含义，需要感悟集合中蕴含的外延原则，即给定一个集合，任何一个元素在不在这个集合中就确定了；一个给定集合的元素是互不相同的，集合中的元素不重复出现。这样只要构成两个集合的元素是一样的，就称这两个集合相等。

理解集合的含义，还需要经历一个用自然语言到用符号语言、图形语言描述集合的过程。例如，教师可以结合几个具体的例子设计这样的活动：试比较用自然语言、列举法、描述法和区间表示集合时，各自的特点和适用的对象。在自然语言描述集合、列举法表示集合、描述法表示集合、区间表示集合和文氏图表示集合的转换中，感受各种语言和方法表示集合的优点及适用对象，体会用集合语言表达数学研究对象的简明和深刻性。一般地，集合A的元素用x表示，所有x的共同的特征性质用P（x）表示，则集合A就能表示成{x│P（x）}。集合A表示成{x│P（x）}意味着，凡具有性质P（x）的对象x都是A的元素，凡是A的元素都具有性质P（x）。

（二）依托集合的关系建立与运算求解

集合之间的关系和运算对学生来讲是全新的内容，但教师可以借助学生已有的知识与经验引发思考，如实数有相等关系和大小关系，你能由实数之间的大小关系，类比想到集合之间的何种关系？你又是如何类比两个数的运算，两个集合之间有什么运算？教师设计这样的数学思考与探究活动，结合具体的问题情境，在类比、概括等数学活动中，建立集合的关系和基本运算，就能有效地帮助学生积累数学抽象的经验、发展数学运算和逻辑推理能力。

又如，集合之间包含关系的建立。在问题“如何类比两个数的关系思考两个集合之间的关系”的引导下，观察如下具体的集合实例。

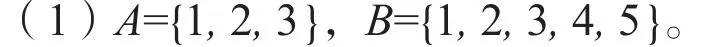
（2）设A是我校高一（1）班的全体学生组成的集合，B是我校全体学生组成的集合。

（3）C={x│x是两条边相等的三角形}，D={x│x是等腰三角形} 。

通过观察上述分别用列举法、自然语言和描述法表示的三组集合，发现每组集合中，第一个集合中的每个元素都属于第二个集合，把两个集合之间的这种关系概括出来就形成子集的概念；进一步可以发现上述（3）中集合D中的每个元素也都属于集合C，这样集合相等的概念自然而生（与实数中的结论“若a≥b且a≤b则a=b”类比）；再进一步，还可以发现上述（1）（2）中至少有一个存在于B中但不属于A的元素，这样真子集的概念应运而生。

如此，在类比思想的指导下，通过观察、分析一个集合中的元素与另一个集合的从属关系，进而概括出两个集合之间的基本关系，并用文字和符号语言加以定义、用图形语言加以表示。学生的抽象概括能力就是在这样具体概念的建立、表征过程中逐步形成的。

（三）依托集合的语言表达与运用

使用集合的语言，可以准确、简洁地表示所要研究的对象，这源自集合蕴含的概括原则和外延原则；依据集合的表示、基本关系和基本运算，我们可以更好地描述所研究的对象之间的关系去解决问题。

首先，教师使用集合语言，引导学生梳理、表达学过的相应数学内容。例如，我们可以用集合语言表示平面几何对象或位置关系。用点P表示平面内的动点，则以点O为圆心，半径为5的圆表示为集合{P│PO=5}；设平面内有△ABC，且点P表示这个平面内的动点，我们可以问学生集合{P│PA=PB}表示什么？属于集合 {P│PA=PB}∩ {P│PB=PC}的点又是什么？我们还可以用集合语言表示平面内两条直线的三种位置关系：①直线l1、l2相交于一点P可表示为l1∩l2={点P}；②直线l1、l2平行可表示为；③直线l1、l2重合可表示为

其次，教师使用集合语言，引导学生描述和解决问题。用集合语言描述问题，可以帮助学生打开分析、解决问题的新思路。例如，学校开运动会，设A={x│x是参加100米跑的学生}，B={x│x是参加200米跑的学生}，C={x│x是参加400米跑的学生}。学校规定，每个参加上述比赛的学生最多只能参加两项，我们就可以引导学生利用集合的运算来说明这项规定，并解释“A∩B”“A∩C”的实际含义。在上述背景下，高一（1）班进行了预赛，共有28名学生参加上述三项比赛，有15人参加100米跑，有14人参加200米跑，有8人参加400米跑，同时参加100米跑和200米跑的有3人，同时参加100米和400米跑的有3人，没有人同时参加三项比赛。我们就可以引导学生借助集合运算的文氏图，求得同时参加200米跑和400米跑的有多少人，只参加400米跑这一项比赛的有多少人，等等。

以课程标准中最基本的核心知识为载体，利用学习过的数学知识分析和解释现实的、数学的、科学的情境中的问题，以蕴含数学知识之中的数学思想方法为指导解决问题，是培养数学学科核心素养的关键过程。

三、进一步思考

笔者认为上述对集合单元育人价值及如何发展学生核心素养的分析，对数学教学有进一步启示。

（1）要重视挖掘有关数学内容对培养学生数学核心素养方面可能的推动与贡献。课程标准根据数学学科特点凝练出的六大数学核心素养，是与具体的数学内容相联系的。鉴于此，挖掘数学内容单元对数学核心素养的贡献，建构与教材单元（章节）内容对应的核心素养细目表，是利用数学的内在力量实现立德树人目标的正确方向。

（2）要设计、选择与数学学科内容特征、数学核心素养相对应的学习方式。数学知识的习得需要与习得知识的科学过程要相匹配，只有这样，知识技能才有可能成为素养。换言之，学什么（知识与技能），怎样学（过程与方法）和学会什么（能力、品格、观念）是一个整体，具有内在的一致性，我们不能把三者割裂开来去行动。 探索与数学学科核心素养目标匹配的学习方式，这是数学教育走向专业化的必经之路。

综上所述，集合作为高中数学课程的起始单元，学生学习本单元的经历和成效，对其学习整个高中数学课程的学习心理、学习方式有重要影响。我们应该尽可能地以义务教育阶段数学课程内容为载体，组织合适的现实情境或数学情境，从中概括出集合、集合的关系和运算等数学对象的一般特征，用自然语言、图形语言、符号语言表达这些数学研究对象，并进行三种语言的转换，展现集合语言的魅力，用这样的数学方式促进学生数学抽象、逻辑推理等核心素养的发展。