基于相邻和语义亲和力的开放知识图谱表示学习

杜治娟 杜治蓉 王 璐

1(内蒙古大学计算机学院 呼和浩特 010021)2(北方工业大学信息学院 北京 100144)3(中国科学技术信息研究所 北京 100038)(nmg-duzhijuan@163.com)

知识图谱[1](knowledge graph,KG)是一种多关系图，节点由实体组成，边由不同类型的关系构成.边的实例是事实三元组〈头实体，关系，尾实体〉(表示为〈h，r，t〉).例如〈爱因斯坦，作者，相对论〉表示“爱因斯坦是相对论的作者”.作为大数据时代最重要的知识表示方式和驱动力，KG可以打破不同场景下的数据隔离，为查询、推荐、预测等实际应用提供基础支持[2].随着应用对语义计算的青睐，将KG中实体和关系转换到低维向量空间的表示学习方法也备受青睐[3-4].典型的方法如TransE[5],ComplEx[6],ConvE[7]，它们存在2个共同的缺陷：

1)前提假设与现实不符.大多数方法假定KG满足闭合世界假设(closed-world assumption,CWA)[8].这就要求所有实体一次性都出现，这对于真实世界的KG来说是不实际的.现实中每天都会有新实体出现，比如DBpedia每天都会有超过200个新实体出现[9].对于这一问题目前有2种解决方案[4].第1种是当新实体出现时重新训练所有数据，显然效率低下和不切实际,特别是遇到大规模KG时；第2种是利用文本知识辅助实体学习，但并非每个实体在现实中都有相应的文本知识.

2)采用复杂的语义交互提高准确性.通常，准确性高的模型，语义交互方式也比较复杂.例如对于图1，TranR[10]认为实体t1,t2,t4语义相似，t5,t6语义不同，为同一关系链接的所有实体设置一个投影矩阵(如Mr1t1,Mr1t2,Mr2t5)来聚拢语义.TransD[11]认为投影矩阵也与实体本身有关，为每个实体也建立了一个投影向量.ConvE[7]认为所有的实体都可能相关，采用二维CNN来捕捉实体和关系之间的语义交互.虽然它们可以提高模型的精度，但矩阵向量乘法或卷积运算也大大增加了训练时间.

为了解决以上问题，首先分析表示学习原理：表示学习模型通过更新实体和关系的初始随机向量来学习它们的向量表示.因此，任何新的实体只能用初始随机向量表示，因为新实体未经过训练，不会通过其他任何实体推理得到.一个自然的想法是用实体间的链接结构推断新实体(1)本文所说的新实体是指仅有新实体本身不在KG中，它所在的任意三元组中的其他2个元素都在KG中的情况.，例如图1中的新实体IsaacNewton用它的邻居(关系,实体)对(work_place,RoyalSociety),(occupation,Physicist)和(live_in,London)联合表示.实际上是可行的，如表1所示.

在数据库表中，一行代表一个实体、一列代表一个属性.图1中如果对实体enew(表1行2)操作，相当于把t1,e1,t6看作是enew的属性，辅助enew；如果对表1中r1列操作，对应到图1，即固定r1求与r1链接的所有尾实体.可以看出，属性可以帮助解释推理实体.这启发我们用邻居(实体,关系)来推断新实体.然而，并非每个邻居都能提供帮助，例如在研究physicist时，doctor degree的贡献很小，但the representative work theory of relativity起着决定性的作用.因此，邻里关系是非常重要的.

在建模时为了增强语义交互而采用的矩阵映射和卷积运算是利用了实体的链接结构对实体进行了语义聚焦.与这一功能等价的操作在模型学习(基于边界的排序准则)过程中也有，即负例采样(将给定三元组中的头或尾实体替换为其他实体，构成新的三元组).从图1的观察来看，一个关系链接的头/尾实体只能属于特定的语义域.当替换的实体来自其他语义域时，模型很容易产生零梯度，进而阻碍实体关系向量表示的学习，而不是优化算法.如图2所示，在训练过程中，传统负例采样时通常会选择点线椭圆圈中的三元组，很容易超出边界，产生零梯度.因此，忽略了边界内的一些负例三元组，如实线椭圆圈所示.为此，可以将语义交互转化为基于语义的负例采样方法，即根据语义级别选择负例，如图1中的t1和t2处于一个语义级别，t1和t4在另一个语义级别，语义级别表示为语义亲和力.

Fig.2 A running example of the vanishing gradient图2 梯度消失运行示例

基于上述观察结果，我们提出了一种基于邻居和语义亲和力感知的开放KG表示学习方法——TransNS.其主要贡献总结有4个方面:

1)针对开放KG表示学习任务，设计了相应的表示学习方法TransNS;

2)选取相关的邻居作为实体的属性来解释推断新实体，相关性由关注机制保证;

3)提出语义亲和力的概念，并采用基于语义亲的负例采样方法SA代替语义矩阵映射和卷积;

4)为了评估所提方法，设计了8个新数据集和1个新的评估任务-解释性可视化.

1 问题形式化定义

在本文中，一个新的实体意味着它不可能在KG中或者训练数据集中出现.在闭合KG中永远不会有新实体；在开放KG中肯定会有新实体，且新实体与KG中至少1个实体和1个关系有直接链接关系.表示学习(representation learning)也叫做嵌入(embedding)，即符号表示向量化.面向闭合KG的表示学习记为CKGE(closed knowledge graph embedding).面向开放KG的表示学习记为OKGE(open knowledge graph embedding).文本被描绘成一系列的词.有文本参与的KG表示学习称为文本辅助的KG表示学习.与给定实体直接链接的(关系,实体)对称为该实体的邻居.本文使用的基本数学符号如表2所示：

Table 2 Mathematical Notations Used in the Paper表2 文中使用的数学符号

表2中〈h,r,t〉表示三元组，e={h,t}表示实体，即头实体h和尾实体t都是实体，可以统一同e表示，r表示关系，它们的列向量用黑斜体小写字母表示，矩阵用黑斜体大写字母表示，下标p表示映射.

形式化定义如定义1～5.

定义1.知识图谱G.知识图谱(knowledge graph,KG)是一个有向图，记为G={E,R,T}，节点是实体，边对应于〈h,r,t〉三元组事实.〈h,r,t〉的每条边r表示存在从h到t的关系r.E和R分别表示实体集合和关系集合，T表示一组事实三元组.

因此，知识图谱KG也可以表示为G={E,R,T}={〈h,r,t〉|h,t∈E,r∈R}.

定义2.新实体enew.如果实体enew不在KG中，或者不在训练数据集Δtrain中，但在测试集Δtest中，则实体enew={e|e∉G∪(e∉Δtrain∩e∈Δtest)}称为新实体.

新实体有时也叫缺席实体或者零样本实体.

定义3.闭合KG.给定KGGC={E,R,T}，如果!∃enew或者∀e={e|e∈E∪(e∈Δtrain∩e∈Δtest)}，则GC称为闭合KG，记为CKG(closed knowledge graph).

根据定义2，闭合KG也可以写为GC={〈h,r,t〉|h,t≠enew,h,t∈E,r∈R,〈h,r,t〉∈T}.

定义4.开放KG.给定KGGO={E,R,T}，e∈{〈e,rG,eG〉，〈eG,rG,e〉},rG∈R,eG∈E，如果∃e={e|e=enew∪e∉E∪(e∉Δtrain∩e∈Δtest)}，则GO称为开放KG，记为OKG(open knowledge graph).

根据定义2，开放KG也可以写为GO={〈h,r,t〉|∃(〈hr,t〉∈T∩((h=enew∩t∈E∩r∈R)∪(t=enew∩h∈E∩r∈R)))}

闭合KG基于闭合世界假设(closed-world ass-umption,CWA)的；开放KG基于世界假设(open-world assumption,OWA).

定义5.语义映射SP.给定一个KGG={E,R,T}，r∈R,e∈E，与实体e直接链接的关系r表示为r→e.关系r的头实体h表示为h→r，关系r的尾实体t表示r→t.ri,rj和ei,ej,i≠j表示不同的关系和实体.语义投射是对语义相似的实体进行语义聚拢操作.语义聚拢也叫投影，是一种线性变换.对于每个实体e={ei|ei→ri∪ri→ei}，投影实体表示为eip=Mriei.每个关系ri都有一个投影矩阵Mri.链接到同一关系ri的所有实体e={ei|ei→ri∪ri→ei}共享矩阵Mri.

2 相关工作

KG表示学习中最经典的方法是TransE[5]和RESCAL[12].TransE[5]的核心思想是向量空间中词汇语义的平移不变性，而RESCAL[12]则基于向量的双线性组合，如图3所示:

Fig.3 The modeling principles of TransE and RESCAL图3 TransE和RESCAL的建模原理

2种模型的原理都很简单，但两者都有缺点.TransE[5]非常擅长建模1-to-1关系，但在处理1-to-n，n-to-1和n-to-n复杂关系方面没有优势(2)对于每个关系r，平均链接的头实体h(或者尾实体t)的平均个数低于1.5，则参数被标记为1，否则为n..因为，当一个关系r链接多个实体ek,k=1,2,…,i,…,j,…时会出现多个实体重合的情况，即ei=ej,i≠j.同理，当2个实体间有多重关系时，多个关系也会重合.RESCAL[12]有很多参数，因为它有矩阵向量乘法，且优化整个Mr.为了打破这些限制，它们有许多变种.

基于RESCAL[12]，LFM[15]仅优化非零元素，DistMult[16]使用Mr的对角矩阵来减少参数，但这种方法只能建立对称关系.为了解决这个问题，ComplEx[7]用复数代替实数，并在计算双线性映射之前采用尾实体嵌入的共轭，三元组的得分是双线性映射输出的实数部分.ComplEx[7]的等价物是HolE[17]，它使用点积代替张量积，并采用h和t之间的循环相关来表示实体对，即

HolE[17]在非交换关系和等价关系上优势很大，并且可以通过快速傅里叶变换加速计算.

此外，还有继承了平移原理与双线性原理优势的EAE[18]；利用神经网络原理的SME[19],SLM[20],NTN[20],ProjE[21]和ConvE[7]，它们需要大量三元组参与训练，并不适合稀疏的KG[5]；利用路径知识辅助学习的PTransE[22],PaSKoGE[23],Gaifman[24],CKRL[25]，它们需要选择合适的路径；利用文本知识辅助学习的方法DKRL[26],TEKE[27],SSP[28]，它们需要额外的文本知识，这一点实际中实现起来较困难，因为并非每个实体在现实中都有相应的文本知识.

3 TransNS方法论

为了适应新实体和降低语义交互的代价，我们选取相关的邻居作为实体的属性来推断新实体，并在学习阶段利用实体之间的语义亲和力选择负例三元组来增强语义交互能力，而不是在建模时执行语义投影和卷积操作.这种方法被命名为TransNS，模型框架和评分原则如图4和5所示:

Fig.4 TransNS embedding learning framework图4 TransNS表示学习框架

Fig.5 Scoring principle of SAL图5 SAL打分原则

图4包括2个关键组件：1)基于语义亲和力的负例三元组采样；2)将邻居集成到实体嵌入学习过程.这2个组件不是独立的，而是相互驱动的.前者贯穿始终，直到后者完成为止.后者分为2个阶段：1)依据邻居解释学习实体的表示；2)度量待测三元组的可信度.

3.1 基于语义亲和力的嵌入

图1表明，实体之间的语义距离可以通过实体之间的链接结构来粗略区分，这种粗略的语义距离被定义为语义亲和力(semantic affinity，SA).SA分为5个级别，即L1-SA,L2-SA,L3-SA,L4-SA,L5-SA，如图6和定义6～10所示.

Fig.6 An example of the five levels of semantic affinity图6 语义亲和力的5个级别示例

链接结构表示为：给定一个KGG={E,R,T}={〈h,r,t〉|h,t∈E,r∈R}.直接链接被表示为r→e，否则表示为r↑e.(e1,r)直接链接到e2表示为(e1,r)→e2，否则表示为(e1,r)↑e2.ri,rj和ei,ej,i≠j表示不同的关系和实体;h→r→t表示关系r链接的头尾实体.

定义6.一级语义亲和力L1-SA.给定2个三元组：〈hi,ri,ti〉,〈hi,ri,tj〉∈G，∃(hi,ri)→ti∩(hi,ri)→tj，如图6(a)所示，则称ti和tj满足一级语义亲和力L1-SA.

定义7.二级语义亲和力L2-SA.给定2个三元组：〈hi,ri,ti〉,〈hj,ri,tj〉∈G,∃hi→ri→ti∩hj→ri→tj，如图6(b)所示，则称ti和tj满足二级语义亲和力L2-SA.

定义8.三级语义亲和力L3-SA.给定2个三元组：〈hi,ri,ti〉,〈hi,rj,tj〉∈G,∃hi→ri→ti∩hi→rj→tj，如图6(c)所示，则称ti和tj满足三级语义亲和力L3-SA.

定义9.四级语义亲和力L4-SA.给定一个三元组：〈hi,ri,ti〉∈G,∃hi→ri→ti，如图6(d)所示，则称hi和ti满足四级语义亲和力L4-SA.

定义10.五级语义亲和力L5-SA.给定2个三元组：〈hi,ri,ti〉,〈hj,rj,tj〉∈G,∃hi→ri→ti∩hj→rj→tj，hi≠hj,ri≠rj,ti≠tj,如图6(e)所示，则称ti和tj满足五级语义亲和力L5-SA.

由于实体之间存在语义距离，同一关系链接的头或尾实体只能属于特定的语义域.当替换的实体来自其他语义域时，模型很容易导致事实三元组和替换的三元组之间产生较大的能量差距.当超过能量间隔上限时，该替换的三元组将得不到训练信号.相比之下，如果替换的实体来自相同的语义域，则情况会好一些.为此，替换的实体优先选择具有强语义亲和力的实体，这个方法叫做基于语义亲和力的负例采样，记为SA.这样做可以替代语义投影和卷积计算实现实体的语义交互.然后评分函数仅使用轻量级的平移原理:

(1)

式(1)的原理如图5所示.我们命名这个表示学习方法为SAL.

为了学习这个模型，我们将式(1)转化为最优化问题，并在训练集上使用基于边界的对排序损失进行训练:

(2)

采用SGD[29]可以很容易地优化求解式(2).其中，γ是边界，Δ和Δ′分别是正例集合和负例集合，Δ中的每个事实三元组〈h,r,t〉都来自训练数据集，Δ′中的负例是由SA采样策略从正例集合Δ中采样产生:

Δ′={(h′,r,t)|h′∈E∪(h,r,t′)|t′∈E},

(3)

3.2 集成邻居的解释学习

TransNS使用邻居增强表示学习的可解释性和适应开放知识图谱.实体e的邻居是以e为头实体的(关系，尾实体)对，形式化为定义11.

定义11.实体的邻居.给定KGG={〈h,r,t〉|h,t∈E,r∈R},实体e∈E的邻居是与其直接链接的(r,t)对的集合，记为N(e)={(r,t)|r∈NR(e),t∈NE(e),〈e,r,t〉∈G}.NE(e)是邻居实体的集合,NR(e)是邻居关系的集合，r是e的(出边)关系，t是通过r与e直接相连的实体，即邻居实体.

给定三元组〈h,r,t〉对，实体h的第i个邻居的NCAαtti定义为

(4)

其中，Corr((r,t),Ni(h))是度量(r,t)和N(h)相关性的函数:

Corr((r,t),Ni(h))∝P((r,t)|Ni(h))(rTrhi),

(5)

P((r,t)|Ni(h))用于度量(r,t)和Ni(h)的相关性，rTrhi表示r和rhi的相关性.

在此基础上，给出实体h通过邻居学习向量表示的计算为

(6)

类似的方法可以获得实体t的嵌入表示.接下来，使用从邻居学习到的h,t和等待训练的r一起进行培训(如式(1))，以测量三元组〈h,r,t〉的可能性.

TransNS的整体训练目标：

Loverall=Lneg+Ltri,

(7)

其中，Lneg与邻居相关，由式(7)代替式(2)中的fr(h,t)得到，Ltri与三元组〈h,r,t〉相关，由式(2)得到，为了降低计算代价，这里借鉴负采样法[30]对式(4)进行了合理的逼近.TransNS部署如算法1所示：

算法1.知识图谱表示学习算法TransNS.

输入：训练集Δ、实体集E、关系集R、嵌入维度n、边界γ和学习率α；

输出：实体和关系的向量表示h,r,t.

② while not reach at loop number or optimal MR value do

③Δbatch←sample(Δ,b)；/*采样一个最小批量大小b*/

④Tbatch←∅；/*初始化三元组对*/

⑤ for 〈h,r,t〉∈Δbatchdo；

/*通过SA采样策略对三元组进行损坏采样*/

⑦Tbatch←Tbatch∪{〈(h,r,t〉),(h′,r,t′)}

⑧N(e)←{(r,t)|r∈NR(e),t∈NE(e),〈e,r,t〉∈G}

/*构建实体e的邻居*/

⑨ end for

⑩ Update embeddings w.r.t.

fr(h′,t′)]+；

算法2.SA：基于语义亲和力的负例采样策略.

/*以替换尾实体为例，替换头实体类似*/

输入：训练集Δ、实体集E、关系集R、嵌入维度n、边界γ和学习率α；

输出：实体的嵌入表示t.

① for 〈h,r,t〉∈Δbatchdo；

② Givenh→r

③ ifL1-SA(t|h→r)≠∅ then

④corr_t=rand_max(L1-SA(t|h→r))

⑤ else if thenL2-SA(t|h→r)≠∅ then

⑥corr_t=rand_max(L2-SA(t|h→r))

⑦ else ifL3-SA(t|h→r)≠∅ then

⑧corr_t=rand_max(L3-SA(t|h→r))

⑨ else ifL4-SA(t|h→r)≠∅ then

⑩corr_t=rand_max(L4-SA(t|h→r))

/*对称关系*/

corr_t=rand_max(entityTotal)

3.3 讨 论

与其他代表性的KG表示学习模型相比，我们的SAL和TransNS有很多优势.我们从7个方面对比各种典型模型,如表3所示.

在实体语义、关系链接实体的数量以及实体之间的链接结构等方面，TransE[5]和ComplEx[6]都没有考虑其中的任何一个.TransD[11]考虑了L2-SA.ConvE[7]认为任何实体都是相互关联的.TranSpars[14]在建模时会考虑到L4-SA和数量特性.我们的SAL和TransNS在训练中使用了5级SA，取代了TransD[11],TranSparse[14]和ConvE[7]的语义投影和卷积.TransNS还利用邻居来增强嵌入式学习的可解释性.

就复杂性而言，TransE[5]和SAL最简单，两者都只有向量加法和减法.TranSparse[14]，ComplEx[6]和ConvE[7]要复杂得多,它们具有矩阵向量乘法，尤其是ConvE[7]具有2D卷积运算.尽管TransD[11]没有矩阵向量乘法，但它的每个实体都有一个投影向量.因此，它的复杂性与实体数量成正比.当然，最复杂的是TransNS，毕竟使用链接结构.但是，它对新实体的可解释性和适应性是前所未有的.总的来说，SAL是平移表示学习的突破，TransNS有望将嵌入式学习推向现实世界.

Table 3 Comparison of Various Models From 7 Aspects表3 从7个方面对比各种模型

4 实验与结果

我们通过在5个传统数据集和8个新数据集(表3)上执行链接预测[5]、三元组分类[13]和邻居选择可视化任务评估我们的SAL和TransNS.选择TransE[5]，TransD[11]，TransSparse(separate，US)[14]，ComplEx[6]和ConvE[7]作为基准对比方法.

表4中#Rel,#Ent和#New分别表示关系、实体和新实体的数量.#Train、#Valid和#Test分别代表训练集、验证集和测试集.WN11,WN11-K,WN18,WN18RR来自于WordNet[31]；FB15k,FB15K-K,FB15k-237来自于Freebase[32].WN11-K是WN11的子集;WN18RR是WN18的子集;FB15k-237和FB15K-K是FB15k的子集.WN18RR和FB15k-237从原始数据集中删除了反向关系.

Table 4 Experimental Dataset Description表4 实验数据集描述

在新数据集中，随机抽样原始测试集的5%，10%，15%，20%的样例以形成新的测试集NewT.在NewT中，三元组的头尾实体有且仅有一个实体不在训练数据集中，并且头尾中的新实体的比例相等.此外，过滤训练数据集中没有邻居的实体.

4.1 部署和度量标准

对于所有数据集，采用小批量SGD[29]最多迭代训练3 000次，嵌入空间维数d={50,100,200,250}，学习率λ={0.0001,0.001,0.01}，边界γ∈[1,6]步长0.5，最小批量处理容量B={1,100,200}，相似度用d={1,2}测量.我们采用3种常见的评估指标：平均排名(MR)、平均倒数排名(MRR)和Hits@10(即有效测试三元组在前10名中的比例)与过滤设置协议，即不考虑任何KG中出现的采用三元组.较低的MR、较高的MRR或较高的Hits@10表示更好的性能.最佳配置由验证集上的MR值决定.

令T={x1,x2,…,x|T|}表示测试集.像TransE[5]一样，对于T中第i个测试三元组xi，采用SA策略替换它的头实体或者尾实体来生成所有可能的负例三元组Δh(xi)(或者Δt(xi)).并以此来检查模型是否分配更高的得分给xi，低的得分给其负例三元组.如果KG中存在已替换的三元组，则该三元组也是正确的，因此在原始三元组之前对其进行排序并没有错.在获得每个测试三元组的排序之前，我们删除出现在训练集、验证集或测试集中所有替换的三元组.这在TransE[5]中称为过滤设置.第i个待测三元组xi的头尾排序分别与依据评分函数fr()替换的头或尾实体相关:

(8)

(9)

其中，I[P]=1当且仅当条件P为真，否则为0.评价指标平均排序(MR)、平均倒数排序(MRR)和Hits@k被定义为

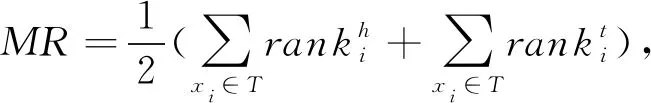
(10)

(11)

(12)

4.2 链接预测

链接预测的目的是预测一个给定事实三元组〈h,r,t〉丢失的头实体h或尾实体t.此任务不需要一个最佳答案，而更多地强调对一组来自KG的候选实体进行排序.在传统数据集上的结果如表5所示、新数据集的结果如表6所示.在表5中，由于实验数据和设置是一致的，所以一些结果为原文发布的结果.Sparse表示TranSparse(separate,US).

Table 5 The Results of Link Prediction on Traditional Datasets表5 传统数据集的链接预测结果

Table 6 Link Prediction Results for TransNS on New Datasets Containing New Entity表6 TransNS在包含新实体的新数据集上的链接预测结果

从表5中观察到结论：SAL的准确性有了一定的提升.在这2个实验数据集中，特别是在WN 18上，SAL接近或优于ConvE[7].在WN 18上，SAL获得最高的MRR分数，在Hits@10上接近ConvE[7](低0.01%)，且远好于TransE[5]和TranSparse[14].而在MR上获得了156的显著改善.在FB15K上，SAL得到了最好的MR，我们可以在WN18RR和FB15K-237上得出同样的结论.但也观察到了一些变化.个别指标除外，SAL在几乎所有指标中都得到最佳值.在这4种数据集上，SAL的预测准确性均优于TranSparse[14]和ConvE[7]，可以解释语义亲和力的优势.研究还表明，基于语义亲和力的负例采样在功能上与语义交互中的投影或卷积等价.

Fig.7 Triples classification accuracies (Prefix Trans is omitted from each model name)图7 三元组分类结果(每个模型名称中省略前缀Trans)

从表5和表6也可以看出TransNS的改善效果，尤其是表6.TransNS的Hits@10评分在WN 18上增加了0.4%～4.8%，在FB15K上MR值提高了2～64.在WN18RR上，TransNS的MR值最小，至少减少140.TransNS的MRR和Hits@10在FB15K-237上最高.就SAL而言，它在8个数据集的每个评价指标方面都有不同程度的改进.特别是在包含新实体的新数据集中，TransNS改进更为明显.结果表明:邻居不仅可以提高表示学习能力，而且可以适应新的实体，即可以很好地用于开放KG.

4.3 三元组分类

三元组分类属于二元分类，其目的是判断给定的三元组〈h,r,t〉是否正确.我们采用WN11,FB15K和它们的变种WN11-K和FB15K-K作为实验数据集来评估模型的准确性.WN11-K和FB15K-K包含新的实体，因此它们只用于测试TransNS的准确性.TransE[5]提供的WN11的测试数据集包含正例和负例三元组.而其他数据集的测试集只包含正例三元组，这里采用文献[14]的方法产生负例.对于验证集，我们用SA策略替换尾(或者头)实体来产生负例三元组.同时，替换后的三元组不能出现在验证集中，否则重新按照SA采样方法选择替换实体.测试数据也进行同样的操作.接下来，基于打分函数计算每个三元组的得分，并由阈值θ区分正确与否.θ由验证数据集中正例与负例之间的距离最大得分决定.最后，如果一个三元组〈h,r,t〉的得分高于θ，则视为正确，否则视为错误.实验结果如图7所示.

图7显示了三元组分类结果，模型名称采用缩写形式.E和S4分别表示TransE[5]和TranSparse(separate，US)[14].Cx,CE,SA和NS分别表示ComplEx[6],ConvE[7],SAL和TransNS.图7表明TransNS在所有数据集上具有明显的优势.例如，与所有基准方法相比，TransNS在WN11上增加0.9%～9.6%，在FB15K上增加0.9%～10.3%，在WN11-K上增加2.3%～11.5%，在FB15K-K上增加2.1%～12.7%，这证明了它采用的5级语义亲和力和实体的邻居是明智的.此外，就新实体的适应性而言，随着新实体的增加，TransE[5]和SAL的表现将迅速下降，但TransNS则不会.这主要是因为新实体未经过训练，仍然保留了TransE[5]和SAL的初始值.

除了TransNS和SAL，ConvE[7]是所有数据集中最好的.这是因为2D卷积相当于增加训练迭代次数，而卷积运算以隐含的形式捕获各种语义.它不如SAL好，因为实验数据不是全连通的.此外，SAL属于与TransE[5]和TranSparse[14]相同的类型(都属于基于平移原理的嵌入表示)，特别是与TransE[5]非常相似.实验结果表明：TranSparse[14]在模型上的实体语义投影操作可以被基于语义亲和力的负例三元组采样方法所取代.与TransE[5]相比，SAL在3个数据集上的性能平均提高了9.93%.所有这些结果都可以证明我们论证的正确性.

4.4 基于关系感知的邻居选择案例研究

此实验旨在确认邻居相关性在预测三元组中的重要性，并可视化TransNS如何通过感知关系为邻居指定权重.因此，从新数据集FB15K-K中选择3个传统方法不易准确预测的示例，如表7所示：

Table 7 The Visualization Result of Neighbors Selection Based on Relation Awareness
表7 基于关系感知的邻居选择的可视化结果

从表7所示的结果中，我们观察到2个结论：

1)基于给定(关系，实体)对中的关系感知，TransNS可以给予更高相关性邻居更大的权重.在第1种情况下，当给定关系place_lived时，只有一个邻居与位置相关，但是这个邻居在top-10中做出正确的结果也发挥了重要作用.在第2种情况下，当给定的关系是profession时，它的5个邻居都表明它的职业是philosophy，它们有助于暗示关系来源.在第3种情况下，当给定的关系是origin时，它的前2个邻居是(place_lived,Orange_County)和(breed_origin,Santa_Ana)，它们也有助于暗示关系来源.但它的邻居(friend,Corbin_Bleu_Reivers)获得的权重最低，因为它们对于给定的关系来源没有任何暗示.

2)TransNS可以将更大的权重分配给具有更多信息的邻居实体.当给定的关系是profession时，最有影响力的邻居是(influenced_by,Aristotle)，比其他邻居，如Metaphysics和Aesthetics与答案Philosopher更相关.在其他情况下，我们也观察到类似的情况.其中，案例2和案例3中权重最大的邻居分别是(institution,University_of_Calgary)和(place_lived,Orange_County)，因为给定的place_lived和origin可以帮助TransNS聚焦于邻居关系institution和place_lived，然后邻居实体University_of_Calgary和Orange_County进一步确定了答案Orange_County.

5 总结与未来工作

本文针对开放KG提出了一种新的表示学习模型TransNS和SAL.SAL采用基于语义亲和力的负例采样方法捕获KG中实体之间的语义，它将语义交互嵌入到训练中，而不增加任何复杂性.TransNS集成集成了实体邻居，可以适应开放KG.实验结果表明：我们的模型优于其他模型.本文中的语义亲和力仅通过实体之间的直接链接来识别.通常，不仅实体的直接邻居可以帮助识别新实体，KG中还有许多间接链接，这些间接邻居也可以起到辅助作用[33].未来工作中可以考虑在语义亲和力测量中引入间接链接关系.此外，本文只考虑仅有新实体本身不在KG中的情况，其实还有2类情况：1)在一个三元组中新实体不在KG中，关系和另外一个实体有且仅有一个不在KG中；2)新实体所在的三元组中的3个元素都不在KG中，如何高效地解决后2种问题也是值得研究的.