基于双模型的MUS求解方法

欧阳丹彤 高 菡 田乃予 刘 梦 张立明

1(吉林大学软件学院 长春 130012)2(吉林大学计算机科学与技术学院 长春 130012)3(符号计算与知识工程教育部重点实验室(吉林大学)长春 130012)(ouyangdantong@163.com)

命题可满足问题(propositional satisfiability problem,SAT)是人工智能领域中的研究热点[1-5],极小不可满足子集(minimal unsatisfiable subset,MUS)和极小修正子集(minimal correction set,MCS)是SAT问题的扩展问题.在现实中许多重要问题可以编码为MUS问题进行求解,MUS的主要应用包括本体中不一致性检测问题[6-7]、关系规范调试问题[8-9]、过度约束的时序分析问题[10]、描述逻辑中的公理精确定位问题[11]、硬件模型验证问题[12]和基于模型的诊断[13]等问题.如何高效求解MUS问题对人工智能的很多领域都有深远意义.

近年来,极小不可满足子集求解问题受到国内外学者广泛关注.早在2005年Bailey等人[14]提出DAA方法,根据MUS与MCS互为极小碰集的对偶性来提高MUS枚举效率,首先利用Grow(依次向上遍历真超集)子过程根据1个可满足的节点求得极大可满足子集(maximal satisfiable subset,MSS),对其得到的补集MCS求极小碰集来得到1个MUS,不断迭代此方法来得到多个MUS.2005年及2008年,Liffiton等人[10,15]在DAA方法的基础上提出了CAMUS方法对MUS进行完备求解,CAMUS方法先计算给定问题的所有MSS,再由MSS求得对应的所有MCS,最后根据对偶性求解出全部MUS.值得注意的是,此方法在较难的问题中可能得不到解.2011年Belov等人[16]提出递归模型翻转方法来提升MUS枚举效率,先由给定的不可满足问题得到1个MCS,利用模型翻转得到1组MCS,直至得到所有MCS,之后根据对偶性求得所有的MUS，此方法由于要多次调用碰集算法，故求解MUS较为耗时.2013年Liffiton等人[17]提出结合哈斯图求解MUS的方法,对于哈斯图Map中的任意一个未被探索的节点,利用Grow或Shrink(依次向下遍历真子集)子过程求解得到1个MSS或MUS.同时在2013年Previti等人[18]提出部分MUS枚举方法,称为eMUS方法,此方法先计算极大模型对应的可满足性,如可满足则得到MSS,继而求得其补集MCS,再求极小碰集得到MUS;若不可满足则直接用MUS提取器求解MUS.2016年Liffiton等人[19]结合eMUS方法对MARCO方法进行了改进,给出极大化模型的MARCO-M方法,此方法针对随机选择节点进行求解的缺点,在哈斯图的未求解空间中利用启发式策略优先选择极大节点进行求解,进而较快地求解得到MUS.为了加快MARCO-M方法求解效率，2016年Zhao等人[20]实现了MARCO-M方法的多种子并行化求解方法,使得MARCO-M方法求解效率有较大提高,但并行化求解方法并没有降低分解后子问题的求解复杂度.随着MUS求解方法的不断改进,许多学者开始研究如何结合MUS求解技术对MCS求解方法进行优化.2018年Narodytska等人[21]在Belov等人[16]递归模型翻转求解MUS方法的基础上给出高效的MCS求解方法,先根据求解得到的1个MUS求出对应的MCS,然后结合递归模型翻转得到其对应的1组MCS,重复迭代上述2步直至得到所有的MCS.

对于MARCO-M方法,它使用1个框架来描述和可视化不可满足性分析方法,就不可满足的约束系统以哈斯图的形式可视化幂集图以及遍历操作.在MARCO-M方法对其之前工作中随机模型进行改进后新提出的极大化模型而言,该模型是利用了在时间上产生类似于最先进的单-MUS方法的第1个输出,这使得在较早期产生解时它是高效的.基于它自上而下的遍历方式,若是实例中MUS解个数很少或都集中在幂集图下半部时,它将在求得首个MUS之后效果不再显著,甚至变差,这是由它自身模型的单一性导致的.

本文在充分分析MARCO-M方法的基础上,对其极大化模型进行改进,给出双模型遍历方法MARCO-MAM方法,对于极大化模型以牺牲MSS求解而只专注于MUS求解的遍历方式,提出了利用MSS求解辅助MUS求解的新想法,并以此增强MARCO-M方法在难以处理实例问题中的稳健性.

1 预备知识

本节首先介绍SAT问题的相关定义,然后介绍其扩展问题MUS和MCS的相关概念,并在最后介绍了MUS和MCS之间的对偶关系.

1.1 SAT问题

SAT问题又称布尔可满足性问题,是一种简单布尔类型的约束可满足判定问题,即判定1个给定的命题公式是否可满足.在命题逻辑的定义中,析取用符号∨表示,合取用符号∧表示.下面给出其相关形式化定义.

定义1.文字[22].给定m个布尔变量x1,x2,…,xm,文字Qi是变量xi或xi的否定(﹁xi).

定义2.子句[22].给定n个互不相同的文字Q1,Q2,…,Qn,子句Ci是文字的析取：Q1∨Q2∨…∨Qn.

定义3.合取范式(CNF)[22].形式如C1∧C2∧…∧Cr的由多个不同子句的合取所组成的公式称为合取范式(CNF).

定义4.SAT问题[22].SAT问题通常是指合取范式CNF的可满足问题,即判定是否存在使得合取公式C1∧C2∧…∧Cr的真值为真的1组变量的赋值.

对于1个给定的合取范式Φ,SAT问题即判断是否存在1组赋值使得公式Φ的值为真：若存在,则称公式Φ是可满足的;否则,是不可满足的.

1.2 MUS和MCS

本节介绍SAT的扩展问题MUS,MSS,MCS问题,并介绍3者之间的互补及对偶的关系.

定义5.MUS[19].称M为不可满足问题Φ的1个MUS,若M⊆Φ,M不可满足,且∀c∈M:M{c}可满足.

定义6.MSS[19].称M为不可满足问题Φ的1个MSS,若M⊆Φ,M可满足,且∀c∈ΦM:M∪{c}不可满足.

定义7.MCS[19].称M为不可满足问题Φ的1个MCS,若M⊆Φ,ΦM可满足,且∀S∈M:ΦS不可满足.

从定义6和定义7的关系可以得出,MSS与MCS互为补集.不可满足问题Φ的任何一个MSS都对应1个MCS,反之亦然.实例的任何MCS都是该实例的MUS集合的极小碰集,并且任何MUS都是MCS的极小碰集[21],即对偶性.下面给出1个实例来介绍MUS,MSS,MCS三者之间的关系.

例1.Φ={s1:(α),s2:(﹁α),s3:(﹁α∨β),s4:(﹁β)},其中,不可满足问题Φ的所有MUS为{s1,s2},{s1,s3,s4},根据其对偶性关系对所有MUS求极小碰集得到所有MCS为{s1},{s2,s4},{s2,s3},又由MCS与MSS的互补关系可以得到所有的MSS为{s2,s3,s4},{s1,s3},{s1,s4}.

2 MARCO-M方法

为了求解给定不可满足问题的所有MUS,则需要判定不可满足问题每一个子集的可满足性,此过程实际上是枚举集合对应其幂集的过程.MARCO-M方法中利用哈斯图枚举,下面先介绍哈斯图.对于给定集合S={1,2,3,4},设它的幂集为P(S),则S的哈斯图幂集可视化如图1所示:

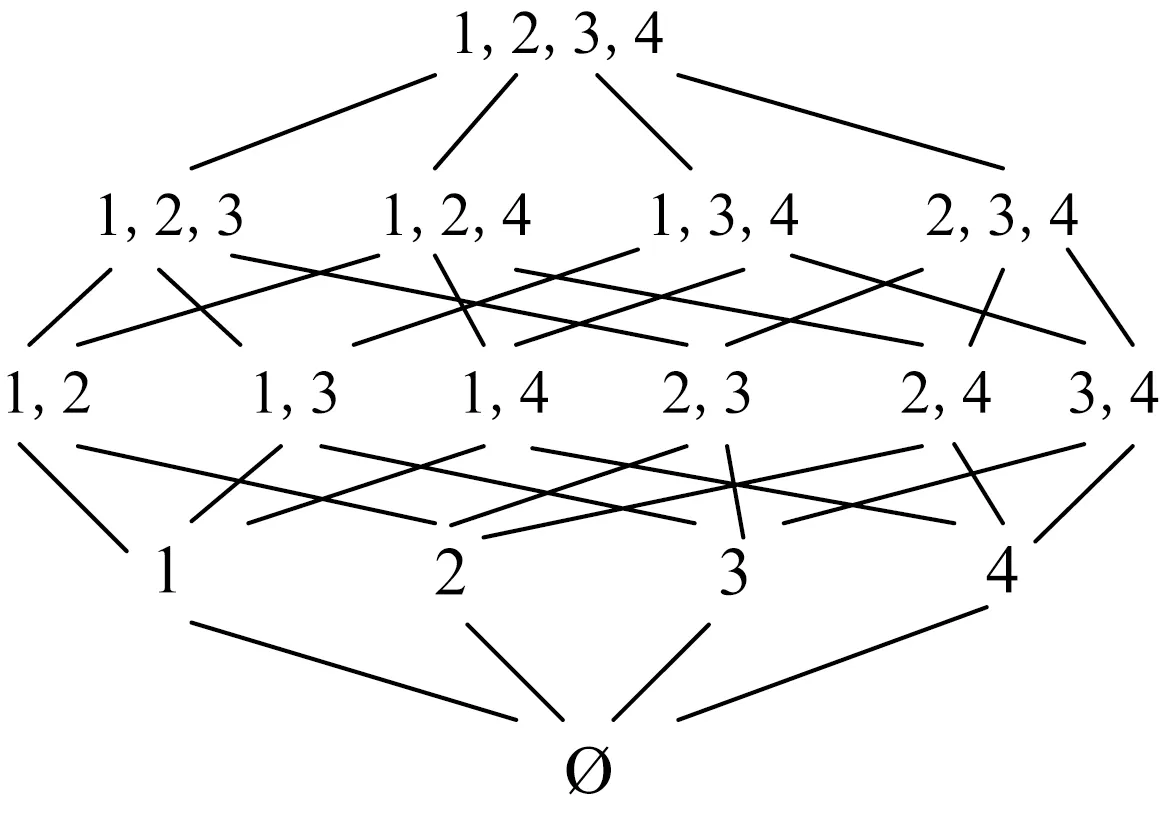
Fig.1 Example of Hasse diagram图1 哈斯图示例

MARCO-M方法基本思想：在求解不可满足问题的所有MUS的过程中,利用哈斯图对求解过程进行模拟.即要求解所有的MUS,只需要遍历哈斯图上的所有节点,对每个节点进行相应的判定就可以得到最后的解.如果当前判定的节点是可满足的,则向上判定其超集的可满足性,直到某个超集节点是不可满足,则此过程中最后一个可满足的节点为MSS,并对MSS对应的所有子集节点进行阻塞,不再访问求解此空间;如果当前判定的节点是不可满足的,则向下判定其子集的可满足性,直到某个子集节点是可满足的,则此过程中最后一个不可满足的节点为MUS,并对MUS对应的所有超集节点进行阻塞,不再访问求解此空间.最后得到所有MUS和MSS.

上面介绍了MARCO-M方法用到的哈斯图和其求解的基本思想,下面介绍MARCO-M方法的伪代码.

算法1.MARCO-M.

输入:不可满足的约束系统C;

输出:C中的极小不可满足集合ΨMUS、极大可满足集合ΨMSS.

①ΨMUS←∅;

②ΨMSS←∅;

③nvars←|C|;

④Map←BoolFormula(nvars);

⑤ While(Map是可满足的)

⑥Seed←GetUepM(Map);

⑦ If(SAT(Seed))

/*极大化模型得到的Seed就是1个MSS*/

⑧ΨMSS←ΨMSS∪Seed;

⑨Map←Map∩BlockDown(Seed);

⑩ Else

算法1中行①②初始化MUS及MSS的解集集合,行③④初始化Map即哈斯图,读取文件中的约束加入Map,在Map可满足时(行⑤),说明Map中至少还有1个节点没有被遍历,则继续遍历,将未遍历节点中的极大节点作为下一次遍历的目标节点也就是种子Seed,每得到1个Seed,就判断它的可满足性.若可满足(行⑦),因为它是极大的,故直接得到1个MSS,将它加入ΨMSS解集(行⑧)并向下阻塞所有子集(行⑨);若不可满足(行⑩),则向下Shrink成1个MUS,将它加入ΨMUS解集(行)并向上阻塞其所有超集(行).极大化模型选取极大种子的目的在于选取的Seed越大它就越可能是不可满足的,且若Seed是可满足,则它直接就是MSS解,省去了Grow的子过程.下面介绍MARCO-MAM方法,并以1个实例运行过程来说明MARCO-MAM方法对MARCO-M方法的改进.

3 MARCO-MAM方法

第2节介绍了MARCO-M方法的基本思想,它在算法1中提出了针对求解所有MUS的极大化模型.MARCO-MAM方法是在此基础上提出的双模型交替求解方法,避免了MARCO-M方法单一极大化模型求解MUS时未有效利用其他优化技术对求解空间进行剪枝的不足.下面给出MARCO-MAM方法使用的双模型交替求解方法,最后再给出1个实例对2种方法进行说明.

MARCO-MAM方法思想：本方法交替求解MUS解及MSS解,利用MSS求解时对应的剪枝来减小MUS搜索的空间,进而提高MUS求解效率,同时也提高MSS求解效率.MARCO-MAM方法在求解中仍然使用哈斯图对求解过程进行模拟.双模型交替即为使用极大化模型-中间模型交替来遍历哈斯图,已知极大化模型是针对求解MUS的,我们提出中间模型用来针对求解MSS,因此使用双模型会得到MUS,MSS交替的解.在求解MUS及MSS的过程中我们仍调用Shrink及Grow子过程,并在每一次得到1个解后对Map进行阻塞以标记已探索空间,直到得到所有的MUS,MSS.下面给出MARCO-MAM方法的伪代码.

算法2.MARCO-MAM.

输入:不可满足的约束系统C;

输出:C中的极小不可满足集合ΨMUS、极大可满足集合ΨMSS.

①ΨMUS←∅;

②ΨMSS←∅;

③nvars←|C|;

④Map←BoolFormula(nvars);

⑤ While (Map是可满足的)

⑥Seed[]←GetUepM(Map);

/*极大化模型得到的Seed_Max*/

⑦ If (SAT(Seed[0]))

⑧s←Grow(Seed);

⑨ΨMSS←ΨMSS∪s;

⑩Map←Map∩BlockDown(s);

算法2相对与MARCO-M方法的改进主要体现在遍历方式及模型的选取上.首先根据极大化模型选取Seed列表中的第1个Seed(行⑥).行⑦中,当Seed可满足时,若Seed由极大化模型得到,则直接作为MSS解,若Seed由中间模型得到,则调用Grow得到1个MSS(行⑧);当Seed不可满足时,根据极大化模型得到1个中间模型加入到Seed列表中(行),作为下一个Seed.在每得到1个解后删除当前Seed(行).下面给出1个实例对这2种方法进行对比.

例2.对于待求解问题Φ={s1:(α),s2:(﹁α),s3:(﹁α∨β),s4:(﹁β)},其对应的哈斯图如图1所示.MARCO-M方法执行实例为:从Map=∅开始执行,当前实例的可满足性需进行判定,GetUepM()在首次执行时会选择P(Φ)中的全集即{s1,s2,s3,s4}作为Seed,即为极大模型.其执行过程为:

步骤1.

选取{s1,s2,s3,s4}为Seed;

SAT({s1,s2,s3,s4})→False(不可满足的);

Shrink({s1,s2,s3,s4})→{s1,s2};

ΨMUS:{s1,s2};

ΨMSS:∅;

Map∧(﹁x1∨﹁x2);

可满足集合:∅;

不可满足集合:{s1,s2,s3,s4},{s1,s2,s3},{s1,s2,s4},{s1,s2}.

步骤2.

选取{s1,s3,s4}为Seed;

SAT({s1,s3,s4})→False(不可满足的);

Shrink({s1,s3,s4})→{s1,s3,s4};

ΨMUS:{s1,s2},{s1,s3,s4};

ΨMSS:∅;

Map∧(﹁x1∨﹁x3∨﹁x4);

可满足集合:∅;

不可满足集合:{s1,s2,s3,s4},{s1,s2,s3},{s1,s2,s4},{s1,s2},{s1,s3,s4}.

步骤3.

选取{s2,s3,s4}为Seed;

SAT({s2,s3,s4})→True(可满足的);

Grow({s2,s3,s4})→{s2,s3,s4};

ΨMUS:{s1,s2},{s1,s3,s4};

ΨMSS:{s2,s3,s4};

Map∧(x1);

可满足集合:{s2,s3,s4},{s2,s3},{s2,s4},{s3,s4},{s2},{s3},{s4},{∅};

不可满足集合:{s1,s2,s3,s4},{s1,s2,s3},{s1,s2,s4},{s1,s2},{s1,s3,s4}.

步骤4.

选取{s1,s3}为Seed;

SAT({s1,s3})→True(可满足的);

Grow({s1,s3})→{s1,s3};

ΨMUS:{s1,s2},{s1,s3,s4};

ΨMSS:{s2,s3,s4},{s1,s3};

Map∧(x2∨x4);

可满足集合:{s2,s3,s4},{s2,s3},{s2,s4},{s3,s4},{s2},{s3},{s4},{∅},{s1,s3},{s1};

不可满足集合:{s1,s2,s3,s4},{s1,s2,s3},{s1,s2,s4},{s1,s2},{s1,s3,s4}.

步骤5.

选取{s1,s4}为Seed;

SAT({s1,s4})→True(可满足的);

Grow({s1,s4})→{s1,s4};

ΨMUS:{s1,s2},{s1,s3,s4};

ΨMSS:{s2,s3,s4},{s1,s3},{s1,s4};

Map∧(x2∨x3);

可满足集合:{s2,s3,s4},{s2,s3},{s2,s4},{s3,s4},{s2},{s3},{s4},{∅},{s1,s3},{s1},{s1,s4};

不可满足集合:{s1,s2,s3,s4},{s1,s2,s3},{s1,s2,s4},{s1,s2},{s1,s3,s4}.

MARCO-M方法仅针对MUS做了改进,在快速求出MUS时,不能兼顾以同样的速度求出MSS,忽视了MSS对于哈斯图遍历求解MUS的辅助剪枝作用,且每次只能标记1次Map,模型较单一.下面给出MARCO-MAM方法在上述相同实例上的求解过程,以说明对MARCO-M方法的优化改进之处,MARCO-MAM方法的执行过程为:

步骤1.

选取{s1,s2,s3,s4}为Seed_Max;

SAT({s1,s2,s3,s4})→False(不可满足的);

选取{s1,s3}为Seed_Mid;

SAT({s1,s3})→True(可满足的);

Shrink({s1,s2,s3,s4})→{s1,s2};

Grow({s1,s3})→{s1,s3};

ΨMUS:{s1,s2};

ΨMSS:{s1,s3};

Map∧(﹁x1∨﹁x2)∧(x2∨x4);

可满足集合:{s1,s3},{s1},{s3},{∅};

不可满足集合:{s1,s2,s3,s4},{s1,s2,s3},{s1,s2,s4},{s1,s2}.

步骤2.

选取{s1,s3,s4}为Seed_Max;

SAT({s1,s3,s4})→False(不可满足的);

选取{s1,s4}为Seed_Mid;

SAT({s1,s4})→True(可满足的);

Shrink({s1,s3,s4})→{s1,s3,s4});

Grow({s1,s4})→{s1,s4};

ΨMUS:{s1,s2},{s1,s3,s4};

ΨMSS:({s1,s3},{s1,s4});

Map∧(﹁x1∨﹁x3∨﹁x4)∧(x2∨x3);

可满足集合:{s1,s3},{s1},{s3},{∅},{s1,s4},{s4};

不可满足集合:{s1,s2,s3,s4},{s1,s2,s3},{s1,s2,s4},{s1,s2},{s1,s3,s4}.

步骤3.

选取{s2,s3,s4}为Seed_Max;

SAT({s2,s3,s4})→True(可满足的);

选取{s2,s4}为Seed_Mid;

{s2,s4}在本步骤Seed_Max中已经被遍历过，不再判断其可满足性;

Grow{s2,s3,s4})→{s2,s3,s4});

ΨMUS:{s1,s2},{s1,s3,s4};

ΨMSS:{s1,s3},{s1,s4},{s2,s3,s4};

Map∧(x1);

可满足集合:{s1,s3},{s1},{s3},{∅},{s1,s4},{s4},{s2,s3,s4},{s2,s3},{s2,s4},{s3,s4},{s2};

不可满足集合:{s1,s2,s3,s4},{s1,s2,s3},{s1,s2,s4},{s1,s2},{s1,s3,s4}.

由例2可以看出,MARCO-MAM方法每次获取双模型后会求得2个解,标记Map两次.在MARCO-M方法中只标记1次,这也使得MARCO-M方法需要5步完成全部的遍历,而MARCO-MAM方法则将步骤减少为3步.MARCO-MAM方法在节省生成Seed的求解器调用的同时,也利用求解得到的MSS对Map进行剪枝,使问题在缩减后的求解空间上进行求解,进而节省总求解时间.

4 实验结果

本节将对MARCO-MAM方法与MARCO-M方法进行比较,并给出2种方法在同样测试用例下的实验结果.实验平台为：64位Ubantu 16.04.3 LTS系统,Intel©CoreTMi5-3470 CPU@3.20 GHz×4.MARCO-MAM方法使用的编程语言为Python,调用C++编写的MUS提取器MUSer2以及MiniSat,其中我们使用到的MiniSat是未经修改的MiniSat求解器[18],本次实验测试用例选用MARCO-M方法[20]所用的标准测试用例见http://www.cril.univ-artois.fr/SAT11/.

表1中列1为测试用例名称,测试选取的求解限定时间分别为2 h,4 h,6 h,8 h,10 h,12 h;列2是MARCO-M方法在各限定求解时间内得到MUS的个数;列3是MARCO-MAM方法在各限定求解时间内得到MUS的个数;为直观表达求解效果更优的方法，对表1中MARCO-M方法与MARCO-MAM方法求解得到的MUS较多的个数用黑体表示(相同个数未做标记).从表1中可以看到MARCO-MAM方法在限定时间内大多数实例求得解的个数都优于MARCO-M方法.

Table 1 Comparison of Enumerating MUS Numbers Between MARCO-MAM Method and MARCO-M Method Under Different Execution Time Limits表1 MARCO-MAM方法与MARCO-M方法在不同执行时间限制下枚举MUS个数的比较

Continued (Table 1)

Note:The data of the unadded unit in the table is the number of MUS solutions,and the time for limiting execution is 2 h,4 h,6 h,8 h,10 h,12 h.Data in bold represent more solutions obtained by this method than the other method.

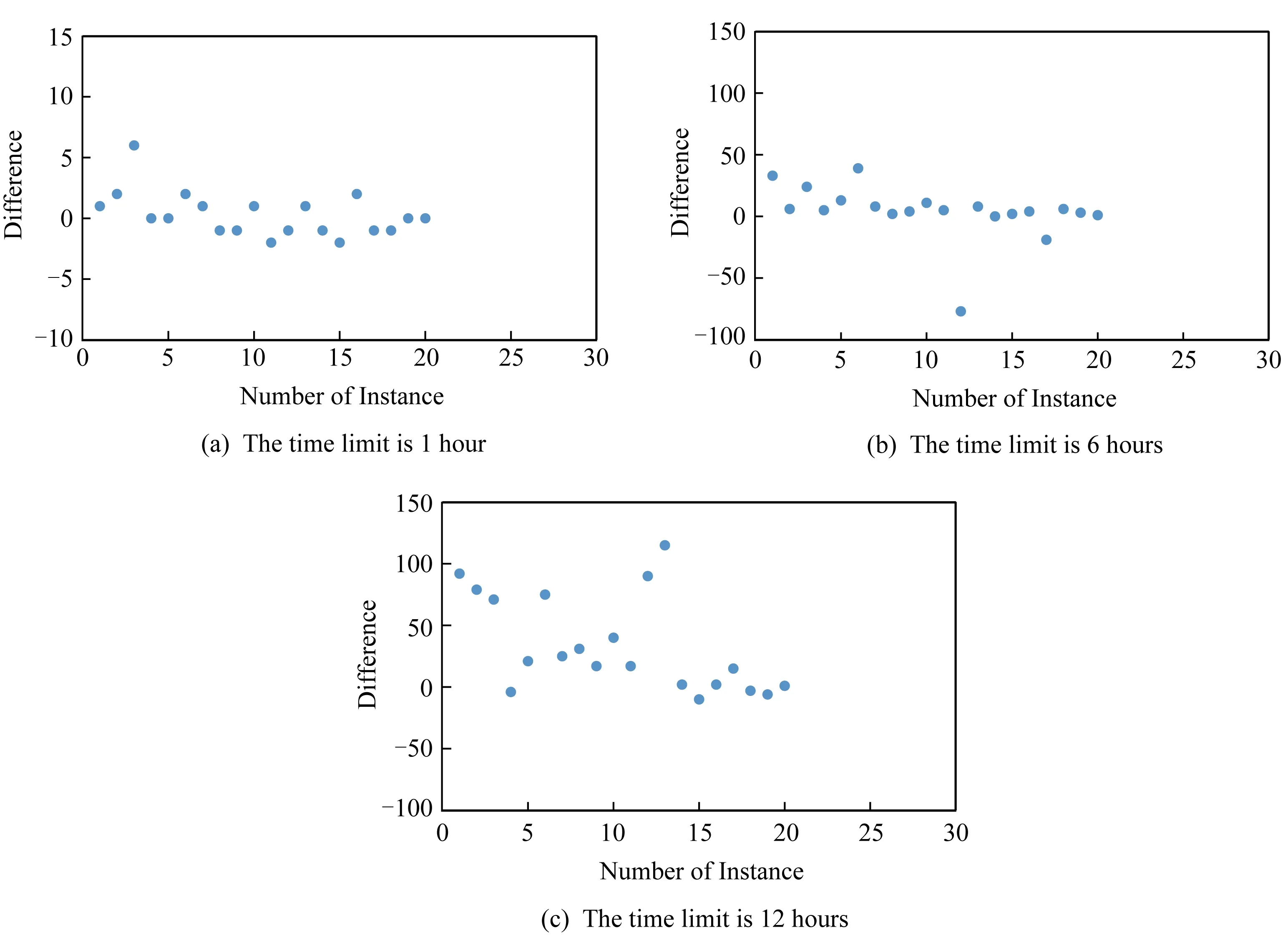
Fig.3 The difference in number of MUS enumeration between MARCO-MAM method and MARCO-M method at different execution times图3 MARCO-MAM方法与MARCO-M方法在不同执行时间下枚举MUS的数量差

图2和图3给出了MARCO -M方法与MARCO -MAM方法在不同时间下求解MUS数量的差值,其中差值是MARCO-MAM方法求解MUS个数减去MARCO-M方法求解的MUS数量.在图3中,差值大于0的数据点为MARCO-MAM方法更优,差值小于0的数据点为MARCO-M方法更优.

在图2中绝大多数点都在坐标轴上方即表示MARCO-MAM方法求解出的MUS数量更多,还有一些点在0刻度线上下浮动,即为与MARCO-M方法相差较小的数据点.

在坐标轴下方少量的点表示有极少情况下MARCO-MAM方法求解MUS数量是少于MARCO-M方法的,这是由于MARCO-MAM方法一部分时间花费在求解中间模型MSS上,即在同一时刻MUS个数少于MARCO-M方法.

Fig.2 The difference in number of MUS enumeration between MARCO-MAM method and MARCO-M method图2 MARCO-MAM方法与MARCO-M方法枚举MUS的数量差

图3给出了时间限定分别在1 h,6 h,12 h求解到的MUS数量差作为表中数据点.从图3(a)中可以看出,在1 h以内,2种方法效率差别不大,MARCO-MAM方法要稍优于MARCO-M方法;在图3(b)中,6 h以内求解得到的MUS数量差较大,在图3(c)中,12 h的时间限制下,MARCO-MAM方法要比MARCO-M方法得到的MUS解数量多近120个解.

MARCO-MAM方法使得MUS的求解越来越快,这得益于MSS的辅助求解及返回2个Seed的模型求解方式,这种方式减少了近一半的因得到Seed模型而调用求解器的次数,进而节省了求解时间.

5 结束语

在对MARCO-M方法深入研究的基础上,针对MARCO-M方法单一极大化模型求解MUS时未有效利用其他优化技术对求解空间进行剪枝的不足,给出基于双模型的MARCO-MAM方法求解MUS.对于MARCO-M方法每次调用求解器只能得到单一模型的问题,MARCO-MAM方法采用了双模型交替的方式,使得求解器返回1个极大化模型及1个中间模型.对中间模型进行求解得到MSS时,利用MSS对应的阻塞空间来对MUS搜索空间进行剪枝,进而提高MUS求解效率;如果中间模型进行求解得到MUS时,则减少了MARCO-M方法中MUS的不可满足迭代求解次数.实验结果表明,在刚开始求解时由于MARCO-MAM一部分时间花费在利用中间模型求解MSS上,此时MUS个数可能会少于MARCO-M方法,但随着求得MSS对应的空间逐渐对MUS搜索空间进行剪枝和减少MUS求解时不可满足迭代求解次数,MARCO-MAM方法求解效率越来越高,尤其在大规模问题或较大搜索空间时MARCO-MAM方法效率提高更为明显.