高中数学核心素养培养途径管窥

甘肃省临夏中学 王建军

培养学生核心素养不仅是“立德树人”的重要体现，而且对学生以后的发展有着积极的推动作用，因此，任课教师应提高认识，正确认识日常教学与核心素养培养间的关系，将核心素养培养作为教学的重点，并认真落实，尤其积极寻找有效途径将培养工作渗透至教学中，实现学生数学学习成绩与核心素养的双重提升。

一、逻辑推理素养培养途径

课程标准明确指出逻辑推理是从事实和命题出发，依据规则推出其他命题的素养，包括从特殊到一般以及从一般到特殊的推理。教学中为培养学生的逻辑推理素养，一方面，有针对性地讲解逻辑推理知识，使学生掌握不同推理类型涉及的方法。如从特殊到一般的推理，包括类比、归纳；从一般到特殊的推理则包括演绎推理。通过讲解使学生掌握逻辑推理基础知识，提高逻辑推理意识。另一方面，围绕数学教学内容创设相关问题情境，鼓励学生思考解答，使学生亲身感受推理过程，深入理解不同推理间的区别，积累与总结逻辑推理经验与技巧，实现逻辑推理能力的显著提升。

题目给出的题干较为简单，要证明等式成立，需要找到n、Sn之间的关系，进行从一般到特殊的推理。

由已知可得a2=3S1=3a1=3，S2=a1+a2=4=4a1。

综上可知，对任意正整数n，Sn+1=4an成立，得证。

二、数学建模素养培养途径

数学建模素养是一种从数学视角出发，抽象数学语言，运用数学方法解决问题的素养。数学建模对学生各方面能力的要求较高，因此，开展培养工作时应有耐心，并长久坚持。一方面，教学中为学生讲解所学的数学模型，包括函数模型、不等式模型、数列模型等。同时，深刻理解讲解数学建模的步骤以及应遵守的原则，打牢数学建模基础知识。另一方面，创设实际问题，要求学生运用所学构建数学模型进行解答，使学生在实践中深化对数学建模的理解，提高其灵活应用能力，实现数学建模素养的提升。

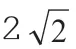
图1

解答该题需要读懂题意，并根据题干中的提示构建相关的函数模型，而后结合函数、导数知识进行求解。

∵BC=xm，则点C到圆环中心的距离为（2-x） m，

三、直观想象素养培养途径

直观想象是一种基于几何直观和空间想象解决数学问题的素养，对学生的想象能力要求较高。为培养学生的直观想象素养，一方面，结合教学内容，引导学生积极联系生活中的物体，想象其几何构造，形成明确的意象并存储在头脑中，加深对点、线、面构成元素及其彼此关系的认识。另一方面，优选训练习题，对学生进行针对性训练，要求学生借助图像分析数学问题，加深其对几何图形的直观认识，构建“数”与“形”之间的关系，以更好地解答数学问题。

该题目不难理解，解答该类题时通常使用数形结合法，训练使要求学生认真读题，找到解题突破口。显然对方程变形得到：f（x）=-a，即在同一直角坐标系中分别绘制出函数f（x）和y=-a的图像，认真观察图像，不难得出正确答案。

由已知可绘制两个函数的图像，如图2 所示：

图2

由 图2 不 难 看 出f（x）+a=0（0＜a＜1）共有5 个根，设由小到大依次 为x1、x2、x3、x4、x5，则x1+x2=-6，x4+x5=6，将x3代入方程，解得x3=1-2a，则不难求出5 个根的和为1-2a，因此，正确答案为C。

高中数学核心素养涉及的内容较多，教学中应做好各方面内容的分析，找到其与数学知识的切合点，将核心素养培养纳入教学内容之中，认真编制教学设计，既要认真做好数学基础知识讲解，保证学生准确记忆、深入理解，又要积极创设相关的问题情境，有针对性地训练学生的能力，促进学生核心素养的提升。