基于局部s变换和极限学习机的柱塞泵滑靴磨损故障诊断

励文艳，程 珩，赵立红，韩 露

(1．太原理工大学新型传感器与智能控制教育部和山西省重点实验室，山西太原 030024；2．太原理工大学机械工程学院，山西太原 030024)

引言

轴向柱塞泵是液压系统的关键部件，其性能好坏对液压系统稳定性起着至关重要的作用。其发生故障会导致振动加剧、噪声增加甚至造成生命安全和财产损失。滑靴磨损是其主要的故障形式之一，严重时导致滑靴脱落，柱塞球头划伤斜盘[1]。因此，快速准确地对滑靴磨损故障进行检测与诊断具有现实的工程意义。

故障诊断主要包括故障特征提取和故障模式识别。故障特征提取的好坏直接关系到模式识别准确率的高低。柱塞泵故障往往通过振动信号表现出来，且故障信号微弱，易受噪声干扰。谭继勇等[2]利用加权峭度值作为优化参数用随机共振方法提取信号冲击成分，具有一定的可行性,但不适用于低信噪比的信号。曾祥辉等[3]提取信号的方差、标准差、峰值等时域特征以及包络信号三层小波分解最大频带能量值共8维特征向量，并结合核超限学习机获得了较高的测试精度，但特征提取的维数较多、计算量较大，且过多的特征量可能降低识别效果。

矩阵奇异值能够反映矩阵背后的真实信息特征，奇异值分解(SVD)可以有效抑制噪声，当信号受到干扰时，奇异值仍可保持良好的稳定性[4]。最大奇异值反映了特征向量空间包含的主要信息量。进行奇异值分解需要构造合适的矩阵，一般的Hankel矩阵无法表征低信噪比的冲击特征信号。s变换提取的特征量对噪声不敏感，受噪声影响较小,且能够充分反映信号的时频信息[5]。因此，采用s变换矩阵作为SVD的分解矩阵可以克服低信噪比对特征提取的影响。将信号进行s变换是将信号在不同频率下进行划分，在不同的故障状态下各频率处能量的分布也必然不同。充分利用s变换矩阵的时频信息是特征提取的一个方向。

在模式识别中，应用最广泛的分类器有蔡伟等[6]采用的支撑向量机(SVM)；邹宪军等[7]采用的BP神经网络；张培林等[8]采用的AdaBoost 算法等。它们共同的缺陷是诊断速度慢、调节参数多、人工干预性强。将极限学习机(ELM)作为柱塞泵模式识别的分类器，优点是速度快、精度高、可以获得全局最优解。

边缘磨损是滑靴磨损的主要磨损形式，且其特征频率与磨损程度有关[9]。本研究针对轴向柱塞泵的正常、滑靴边缘磨损1，2.5，3.5 mm 4种状态进行模式识别。采用振动信号局部s变换矩阵最大奇异值与主要频率能量占比作为液压泵不同状态下的特征向量，并将特征向量输入ELM中进行训练和测试，将不同的特征向量组的识别效果进行定性和定量比较，选择将s矩阵最大奇异值、转轴振动基频能量占比和柱塞振动基频能量占比作为特征向量。最后将ELM与SVM分类结果进行对比，证明所提方法的优越性。

1 算法简介

1.1 s变换

一维连续信号x(t)的s变换定义为：

(1)

(2)

其中，ω(τ-t,f)是与时间τ和频率f有关的高斯窗函数；τ控制高斯窗在时间轴上移动的位置；f为信号的频率。在s变换中，高斯窗的窗宽与f成反比。因此，s变换在信号低频段呈现高的频率分辨率，高频段呈现高的时间分辨率[10]。

一维离散信号x[kT],k=0,1,…,N-1，相应的离散s变换定义为：

(3)

(4)

其中，X[m/NT]是离散信号x[kT]的离散傅里叶变换，N为采样点数，T为采样时间间隔，NT为采样时间。g表示s变换矩阵的第g行。

s变换时频矩阵包含信号的时域和频域信息，且信号时、频域之间具有无损可逆性，运算速度快。

1.2 极限学习机

极限学习机(Extreme Learning Machine，ELM)是一种基于单隐层前馈神经网络(SLFN)的分类算法，它比传统学习算法泛化性能更好。此外，ELM对参数不太敏感，可以更快、更方便地完成数据集的分类识别[11]。

标准的SLFN包含N个任意样本 (xi，ti)∈Rn×m和激活函数g(x)，计算公式为：

=οi(j=1,…,N)

(5)

其中，L为隐层节点的数量，wi=[wi1，wi2，…，win]T和βi=[βi1,βi2, …,βim]T分别为第i个隐藏节点与输入节点、输出节点之间的权重向量，bi是第i个隐藏节点的阈值。

ELM的输出满足下式：

(6)

定义：

H(w1,…,wL,b1,…bL,x1,…，xL)=

(7)

(8)

约束条件为：

(9)

式(9)可以简写为：

Hβ=T

(10)

给定训练集H={(xi，ti)|xi∈Rn，ti∈Rm，i=1，…，N}，激活函数g(x)和隐层节点数L，ELM算法计算步骤为： ① 随机分配输入权重wi和偏置值bi，i=1，…，L； ②计算隐藏层输出矩阵H； ③ 由式(10)反解出矩阵β,β=H+T。

2 实验研究

2.1 实验平台及设备

为了验证基于s变换和ELM进行故障诊断的优越性，搭建试验台采集泵壳的振动信号对滑靴边缘磨损故障进行研究。实验平台系统如图1所示。

1.电机 2.斜盘式轴向柱塞泵 3.二号加速度传感器4.三号加速度传感器 5.一号加速度传感器6.过滤器 7.压力表 8.溢流阀 9.油箱图1 实验平台系统图

主要实验设备及其型号见表1，其中加速度传感器选用可变电容式三轴加速度传感器，3个加速度传感器在泵体上的放置位置如图2所示。其中X，Y，Z为在泵体上建立坐标系的方向，x，y，z为3个三轴加速度传感器的指示方向。

表1 主要实验设备及其型号

图2 3个加速度传感器放置位置及指示方向示意图

2.2 数据采集

振动信号通过加速度传感器进行采集，再通过采集卡NI-USB-6343结合软件LabVIEW储存在计算机中。泵的主油路压力为10 MPa，采样频率为22500 Hz，采集轴向柱塞泵正常状态、滑靴磨损1，2.5，3.5 mm共4种状态的振动信号，采样时间均为1 s，每组状态均采集40组样本。电机额定转速为1480 r/min。在电机额定转速下，转轴振动基频理论值为1480/60=24.67 Hz；实验采用的轴向柱塞泵的柱塞数为9个，柱塞振动基频理论值为(1480/60)×9=222 Hz。

2.3 特征提取

分别将采集的4种状态信号进行Hilbert包络解调，如图3所示。

可以看出，在24 Hz和224 Hz及其倍频处峰值较高。其中，24 Hz与转轴振动基频理论值24.67 Hz对应，224 Hz与柱塞振动基频理论值222 Hz对应。存在微弱偏差原因为泵负载后驱动电机转速略有下降。可以看出包络图无法将四种状态区分开。

将振动信号进行s变换后，分别得到4种状态的s变换时频谱图，如图4所示。对4种状态时频谱中的谱线特点进行观察，更加简单、直观。考虑到转轴振动基频和柱塞振动基频都在低频段，因此设置的变换频率为1～600 Hz。

图3 四种状态Hilbert包络谱图

1) 提取主要频率能量占比

从图4可以看出，4种状态经s变换后的时频谱

图4 各状态s变换时频谱图

中，能量主要集中在24, 224, 448 Hz频率这3个频率附近。仿照频域中的特征能量比[12]，定义s变换时频域的主要能量占比：

(11)

其中，f1～f2为单条谱线上的主要频率取值范围，n表示s变换矩阵的频域点数，即矩阵的行数；N表示s变换矩阵的时域点数，即矩阵的列数；st_matrix为s变换矩阵。

计算以24，224，448 Hz为主的谱线能量在时频域中能量占比：

(12)

(13)

(14)

2) 提取矩阵最大奇异值

矩阵奇异值分解(SVD)公式为：

(15)

其中，λi(i=1, 2, …,k)为AAT的特征值，即为矩阵A的奇异值；Ui、Vi为AAT、ATA相应特征值的特征向量。矩阵最大奇异值为：

λmax=max(λ1,λ2,…,λk,0,…,0)

(16)

3 实验结果分析

每种状态40组样本，20组训练样本，20组测试样本。提取每种状态的FER1、FER2、FER3和λmax，并对其20组训练样本的4个特征向量进行分析。所有计算分析均在MATLAB平台实现。

3.1 特征向量组定性分析

将FER1、FER2作为特征向量，组成一个二维特征向量组，4种状态的二维聚类效果如图5所示。可以看出，此二维特征向量可以完全将状态1区分开，但其他3种状态仍有部分混淆。

图5 二维聚类效果图

因此，选择在此基础上再增加一组特征向量，形成三维特征向量组，以提高分类效果。图6a为增加特征向量FER3后的三维聚类图，图6b为增加特征向量λmax后的三维聚类图。可以看出，图6a和图6b基本可以将这4种状态区分开，但图6b比图6a的聚类效果更好，各种状态分布更加集中。

图6 各种状态三维聚类图

3.2 特征向量组定量比较

为进一步定量比较以上1组二维特征向量和2组三维特征向量的聚类效果，分别将其20组训练样本、20组测试样本输入ELM中进行训练和测试。

ELM的隐层神经元激活函数选为径向基函数。为避免偶然性，每种结果均取20次平均值。最后获得的分类精度如表2所示。

表2 各特征向量组ELM测试结果对比

从测试结果可以看出，二维特征向量FER1、FER2测试精度为91.25%，表明FER1和FER2是两个主要的特征向量，但测试精度仍有待提高；当增加特征向量FER3，形成三维特征向量组时，测试精度达到了95.94%；将增加的特征向量FER3换成λmax时，测试精度可达99.06%，明显高于其他两个特征向量组。结果说明将FER1、FER2和λmax作为反映4种状态的特征向量具有可行性。

3.3 模式识别算法比较

将选用的特征向量组FER1、FER2和λmax输入SVM中进行训练，当选用高斯径向基核函数时可以获得较高的诊断精度，最后将诊断结果与本研究选用的分类器ELM比较，结果见表3。

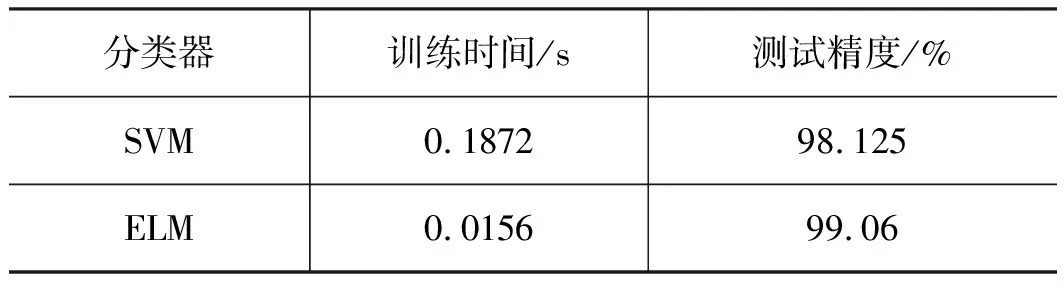
表3 不同分类器测试结果

测试结果表明，ELM相较于SVM训练速度更快、测试精度更高。由于SVM算法需要调节的参数较多，因此所需的时间要比表中的数值更大；然而两者在测试精度上相差不大，进一步表明特征向量选取的有效性。

4 结论

通过不同特征向量组之间定性和定量比较可以看出，选择局部s变换矩阵转轴基频、柱塞振动基频处的能量占比和矩阵最大奇异值作为故障特征向量诊断精度更高，可达99.06%。不同分类器诊断结果表明，ELM分类算法相较SVM有更快的诊断速度和更高的诊断精度。将局部s变换和ELM分类算法相结合进行柱塞泵滑靴磨损故障诊断，可以用较少的特征向量获得较高的诊断精度。