基于线性跟踪微分器的数字阀电机控制系统

(北京精密机电控制设备研究所，北京 100076)

引言

本研究的数字阀与传统的伺服阀最大的区别是取消了液压放大级，采用了伺服电机加丝杠的方式直接驱动阀芯，其具有高频响、大流量、抗污染能力强等优点。在实际使用中，系统对数字伺服阀动态提出了较高的要求，且滑阀液动力的存在制约了数字伺服阀动态的提高。结合数字伺服阀的原理，整阀动态水平由其驱动机构动态性能决定。

驱动机构的动态性能则取决于伺服电机的动态特性，传统的伺服电机控制算法一般采用三闭环控制[1]，电流环、速度环采用比例积分控制，位置环采用纯比例控制，在实际调试中发现，为了提高位置环的带宽，需要增大比例系数。但是随着给定信号频率的加快，比例系数过大会引起很大的超调甚至振荡，这就是经典调节理论中快速性和超调之间的矛盾。二阶线性跟踪微分器的引入很好的解决了这一矛盾，从跟踪微分器的频率特性可以看出，其在通带内具有较小的相移，且不产生谐振。能保证有较短的过渡过程而不出现超调[2]。

传统二阶跟踪微分器通常和状态观测器结合使用，但是存在多参数需要调节的难度。本研究对传统跟踪微分跟踪器进行了简化，由于液动力带来的负载扰动较小，所以去除了状态观测器。有效降低了多参数调节的难度，同时很好的保证了系统动态性能，通过系统仿真和实验验证了该控制策略的有效性。

1 数字伺服阀基本原理

其以永磁同步电机作为电/机转换器，采用丝杠副将电机输出转角转换为直线位移，进而直接驱动滑阀阀芯滑动，最终输出流量。

图1为整阀结构简图，虚线框内为驱动机构，图2为其原理框图，可以看出驱动机构的特点为：

(1) 采用电机角度闭环控制，位移输出精度高、分辨率好；

(2) 整阀的动态特性取决于驱动机构的动态特性。驱动机构的动态特性受电机和丝杠转动惯量等参数影响。

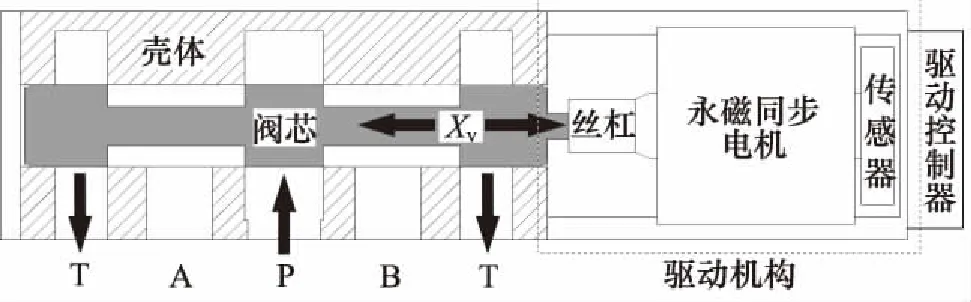
图1 直驱数字伺服阀的结构简图

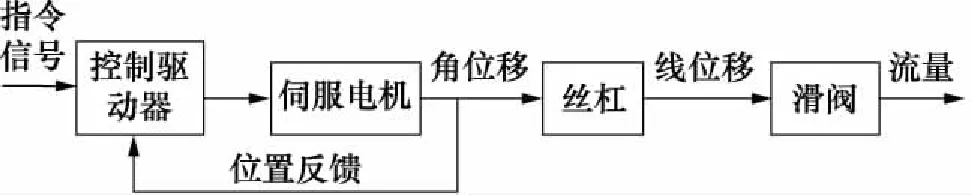
图2 直驱数字伺服阀的原理框图

2 机械传动模型建立

数字伺服阀的机械传动部分主要由电机和滚珠丝杠组成，电机旋转带动丝杠的螺母旋转，进而让旋转运动转化成直线运动。依据动力学方程：

(1)

考虑到机械结构的弹性，负载转矩与输入输出角位移之间的关系可表示为：

TL=KL(θi-θo)

(2)

式中，TL—— 负载转矩

JL—— 折算到丝杠上的转动惯量

θ0—— 丝杠的输出角位移

θi—— 丝杠的输入角位移

BL—— 折算到丝杠上的黏性阻尼系数

Tgr—— 折算到丝杠上的干扰转矩，主要为驱动机构的负载力

KL—— 折算到丝杠上的扭转刚度

在负载扰动Tgr为0的情况下，对式(1)、式(2)进行拉氏变换可得：

(3)

设滚珠丝杠的传动比为i,则：

(4)

由式(3)、式(4)得出电机角度和丝杠输出位移的关系式为：

(5)

图3为采用传统PI控制的直驱式数字伺服阀驱动机构的传递函数框图，由图可以看出，伺服系统是一个高阶多变量的系统，速度环的响应远小于电流环，电流环是速度环的一个内环，经过电流调节器校正后，电流环的闭环传递函数可以等效为一个一阶惯性环节，那么速度环的控制对象为一个惯性环节和积分环节的串联。位置环的响应远小于速度环的响应，即位置环的开环传递函数的截止频率比速度环的截止频率要低很多，所以可以将速度环等效成为一个一阶的惯性环节[3]，那么位置环的开环传递函数等效为一个惯性环节和积分环节相互串联的模型，即位置伺服系统的开环传递函数为式(6)，其中Tw与电机转动惯量成正比，由式(6)可以看出，位置伺服系统的带宽主要由电机和丝杠的转动惯量决定。

(6)

3 自抗扰控制技术原理

自抗扰控制技术原理如图4所示，它主要由三大

图3 数字伺服阀驱动机构控制结构框图

图4 自抗扰控制技术原理框图

模块组成，跟踪微分器、扩张状态观测器、状态误差反馈控制律。跟踪微分器的输入是位置指令，输出是跟踪位置和跟踪位置微分；扩张状态观测器的输入是位置反馈和状态输出；输出是观测位置、观测位置的微分和观测扰动；状态误差反馈控制律根据位置误差、位置微分误差计算输出作速度环的给定。如文献所述，自抗扰控制技术引入了状态观测器能够对扰动实时进行补偿，同时跟踪微分器能够准确跟踪误差及误差的微分值，很好的改善了系统的性能。但是它需要调节的参数非常多，调试较为困难，在参数不当的情况下起不到很好的改善效果。

4 跟踪微分器简化与控制原理

数字伺服阀的工作特点是小角度的位置随动系统，一般给定的位置指令为正弦信号，要求数字伺服阀带宽越高越好，所以应该通过改进控制算法来提高系统动态响应。同时数字伺服阀在工作过程中受到的扰动主要来自于液动力，由于流体的连续性，其对系统的扰动也是连续存在的，所以扩张观测器的存在的意义不大。基于数字伺服阀的工作特点，为了降低多参数调节的难度，去除状态观测器。简化后的线性跟踪微分器如图5虚线框所示，控制系统结构框图如图5所示，采用传统的三环结构，位置环、速度环和电流环，其中位置环采用去除状态观测器的跟踪微分器结构。

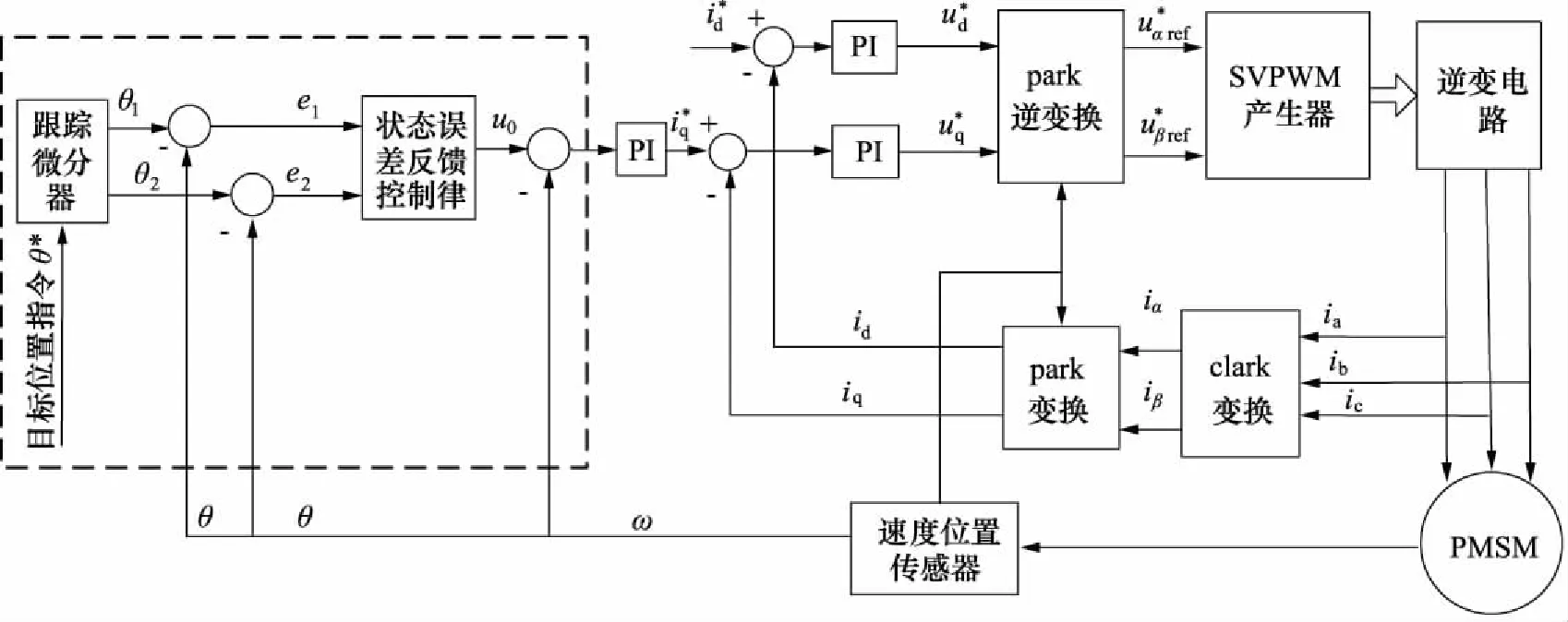
图5 引入跟踪微分器的控制系统框图

5 具体程序实现

在自抗扰控制算法中，二阶跟踪微分器的表达式为：

(7)

(8)

对其离散化后：

θ1(k+1)=θ1(k)+Tθ2(k)

(9)

θ2(k+1)=θ2(k)-Tk1(θ1(k)-θ*(k))-

Tk2θ2(k)

(10)

e1(k)=θ1(k)-θ(k)

(11)

e2(k)=θ2(k)-θ(k)

(12)

对于固定幅值，不同频率的正弦信号，状态误差反馈控制律采用线性叠加的方式，则：

u0(k)=kae1(k)+kbe2(k)

(13)

结合式(11)、式(12)、式(13)得：

u0(k)=ka[θ1(k)-θ(k)]+kb[θ2(k)-θ(k)]

(14)

式中，ka,kb为可调参数；θ1(k)，θ2(k)，θ(k)分别为位置跟踪指令信号，位置跟踪指令信号的误差，位置反馈信号。u0(k)作为速度指令给定信号，相比于扩张状态观测器的多参数调节，该表达式只需要调节ka和kb，极大的降低了参数调节难度。

6 仿真实验

搭建MATLAB/Simulink模型，仿真用驱动机构主要参数如表1所示，分别对传统PI和跟踪微分器进行了仿真并绘制了系统开环传递函数的波特图，如图6所示，曲线1是采用传统PI绘制的波特图，曲线2和>曲线3是调节不同的ka和kb参数绘制的波特图。从图中可以看出，采用跟踪微分器能够在系统不超调的情况下，有较小的相位滞后，有效解决了传统PI快速性和超调之间的矛盾。

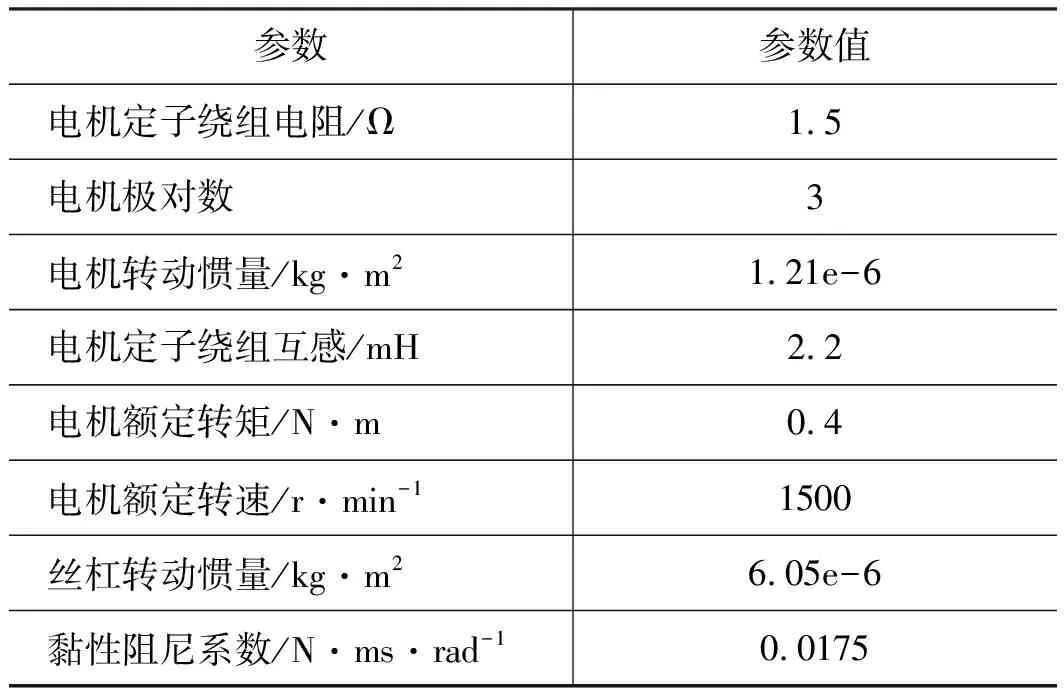
表1 试验所用驱动机构参数

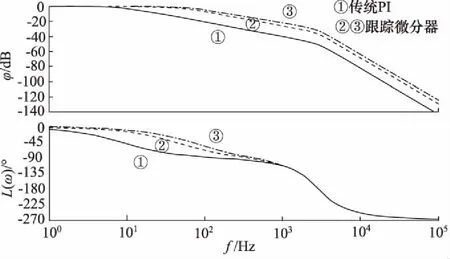
图6 系统开环传递函数波特图

7 系统实验

驱动机构所用控制驱动器控制芯片采用TI公司的32位浮点性DSP，型号为TMS320F28069,功率驱动模块采用DRV8332,PWM中断频率为10 kHz，位置环和速度环10倍频于电流环，系统硬件结构框图和控制系统实物图如图7、图8所示。

图7 控制系统硬件结构框图

图8 控制系统实物图

对控制系统输入幅值为±45°正弦模拟指令信号，不断增加模型信号频率，观察给定位置指令、实时反馈位置、速度给定、实时速度反馈信号。观察幅值衰减和相位滞后情况。实验中发现，采用传统PI存在动态性能和超调之间的矛盾。图9为在传统PI下位置指令和响应曲线图，在保证系统稳定不振荡的参数情况下，当输入指令信号频率超过30 Hz时，相位滞后较为明显。引入跟踪微分器后的观测曲线如图10、图11所示。从图10中可以看出，在输入指令信号为50 Hz时，反馈指令幅值有微小衰减，相位滞后30°。图11中曲线1和曲线2为速度给定和速度反馈曲线，在输入指令信号为50 Hz时，最高速度已经为1500 r/mmin，已经充分发挥了速度跟随的空间。

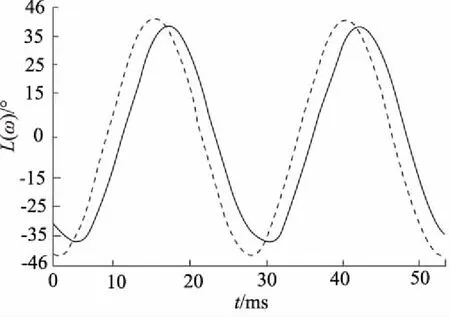
图9 传统PI位置指令及响应曲线图

图10 引入跟踪微分器位置指令及响应曲线图

图11 引入跟踪微分器速度指令及响应曲线图

8 结论

本研究介绍了一种数字阀电机控制系统的控制算法，通过机械传动模型建立、仿真模型建立、程序算法设计以及仿真和实验验证，验证了其良好的性能，可以满足数字阀性能要求。