事件空间中非保守系统的一类拟分数阶Noether定理

王泽，张毅

(1. 苏州科技大学数理学院，江苏 苏州 215009；2. 苏州科技大学土木工程学院，江苏 苏州 215011)

分数阶微积分为解决非保守动力学问题提供了一个重要工具[1-2]。2005年，El-Nabulsi依据Riemann-Liouville分数阶积分的定义提出了建立非保守系统动力学模型的一个方法[3]，并进一步推广到基于按指数律拓展的分数阶积分和按周期律拓展的分数阶积分情形[4-5]。由该方法建立的非保守动力学模型可称为El-Nabulsi拟分数阶模型。张毅等[6]提出并建立了拟分数阶模型下Birkhoff系统的Noether对称性理论，文献[7]将结果推广到基于按指数律拓展的分数阶积分情形。龙梓轩等证明了拟分数阶Lagrange系统和拟分数阶Hamilton系统的Noether定理[8-10]。张孝彩等[11]研究了拟分数阶Lagrange系统的Lie对称性与Hojman守恒量。文献[12-16]研究了基于El-Nabulsi拟分数阶模型非保守系统的对称性摄动与绝热不变量。但是，关于事件空间中基于El-Nabulsi拟分数阶模型的非保守动力学及其对称性研究尚没有见到报道。本文将研究事件空间中El-Nabulsi拟变分问题及其动力学方程，建立事件空间中按周期律拓展的拟分数阶模型下完整非保守系统和非完整非保守系统的Noether定理。

1 事件空间中按周期律拓展的拟分数阶变分问题

设f(t),t∈[a,b]是连续函数，按周期律拓展的α阶分数阶积分定义为[5]

(1)

(2)

不失一般性，以下仅讨论余弦函数情形。考虑由n个广义坐标qk(k=1,2,,n)确定的力学系统，其(n+1)维扩充的位形空间，即事件空间，点的坐标是广义坐标qk和时间τ。引入记号

x1=τ,xk+1=qk,(k=1,2,,n)

(3)

其中xs(s=1,2,,n+1)是参数σ的函数，有C2类曲线xs=xs(σ)，使得

(4)

不同时为零，得

(5)

(6)

则事件空间中基于按周期律拓展的拟分数阶变分问题的提法为：求积分泛函

(7)

在固定边界条件

xs(a)=xs,a,xs(b)=xs,b,(s=1,2,,n+1)

(8)

下的极值问题，其中γ是某曲线，Γ是Euler-Gamma函数，0<α≤1，τ是固有时间，t是观察者时间，σ是某参数，τ≠t。

泛函(7)也称为作用量。当α=1时，上述变分问题退化为事件空间中力学系统的经典变分问题。若泛函(7)在xs=xs(σ)上取得极值，则

(9)

由边界条件(8)，有

可得

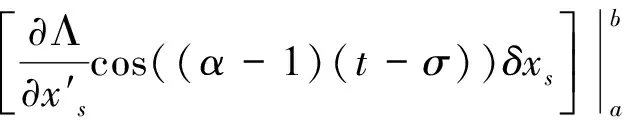
(10)

将式(10)代入式(9)，有

(11)

因为积分区间[a,b]的任意性，所以

(12)

式(12)可称为事件空间中基于按周期律拓展的拟分数阶模型的D’Alembert-Lagrange原理。该原理不仅适用于完整非保守系统，也适用于非完整非保守系统。

对于完整系统，δxs(s=1,2,,n+1)相互独立，因此由式(12)可得

(13)

方程(13)是事件空间中非保守系统基于按周期律拓展的拟分数阶模型的Lagrange方程。

对于非完整系统，设非完整约束为

(14)

约束(14)加在虚位移上的限制条件为[17]

(15)

因为δxs(s=1,2,,n+1)不全独立，由事件空间中D’Alembert-Lagrange原理(12)和条件(15)，运用Lagrange乘子法，得

(16)

其中λβ为约束乘子，方程(16)就是事件空间中非完整系统基于按周期律拓展的拟分数阶模型的Lagrange方程。

2 事件空间中基于按周期律拓展的作用量的变分

引入无限小群变换

(17)

其展开式为

(18)

计算

其中

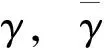
由于非等时变分运算Δ与等时变分运算δ之间成立关系[17]

ΔF=δF+F′Δσ

(21)

这里F为任意函数，因此得到

(22)

利用关系式(22)，式(20)可表为

(23)

由式(17)和(22)，上式可进一步表为

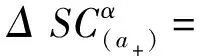
(24)

公式(20)和(24)是事件空间中基于按周期律拓展的作用量泛函(7)的两个变分公式。

3 事件空间中基于按周期律拓展的拟分数阶模型的Noether对称变换

首先，研究事件空间中基于按周期律拓展的拟分数阶模型的Noether对称变换。

定义1 如果作用量泛函(7)是无限小群变换(17)的不变量，那么对每一个无限小变换，始终成立

(25)

可称变换(17)为事件空间中基于按周期律拓展的拟分数阶变分问题的Noether对称变换。

由变分公式(20)，(24)，我们得如下判据。

判据1 对于无限小群变换(17)，若满足条件

(26)

则变换(17)是事件空间中基于按周期律拓展的拟分数阶变分问题的Noether对称变换。

判据2 对于无限小群变换(17)，如果满足r个方程

(27)

则变换(17)是事件空间中基于按周期律拓展的拟分数阶变分问题的Noether对称变换。

由于

(28)

故式(26)归为如下r个方程

(29)

当r=1时，方程(29)给出的Noether等式为

(30)

其次，研究事件空间中基于按周期律拓展的拟分数阶模型的Noether准对称变换。

设Λ′是事件空间中另一Lagrange函数，若满足以下条件(精确到一阶小量)

则作用量泛函(7)是变换(17)下的准不变量。在此情形下的变换(17)称为事件空间中基于按周期律拓展的拟分数阶变分问题的Noether准对称变换。显然

(32)

将式(32)代入式(31)，得

(33)

由于式(33)的左端是一阶小量，因此可用ΔG代替G,而

(34)

所以可得

定义2 如果作用量泛函(7)是无限小群变换(17)的准不变量，即对每一个无限小变换，始终成立

(35)

判据3 对于无限小群变换(17)，若满足条件

则变换(17)是事件空间中基于按周期律拓展的拟分数阶变分问题的Noether准对称变换。

判据4 对于无限小群变换(18)，如果满足r个方程

(37)

其中

ΔG=εμGμ

(38)

则变换(17)是事件空间中基于按周期律拓展的拟分数阶变分问题的Noether准对称变换。

式(36)归为如下r个方程

当取r=1时，方程(39)成为Noether等式

应用以上判据可以求得事件空间中基于按周期律拓展的拟分数阶变分问题的Noether对称变换和Noether准对称变换。

4 事件空间中完整系统基于按周期律拓展的拟分数阶模型的Noether定理

(41)

对于事件空间中完整非保守系统，守恒量可由基于按周期律拓展的拟分数阶变分问题的Noether对称变换或Noether准对称变换求得。故有

定理1 对于事件空间中完整非保守系统(13)，若无限小群变换(17)是基于按周期律拓展的拟分数阶变分问题的Noether对称变换，则系统存在以下r个线性独立的守恒量

(42)

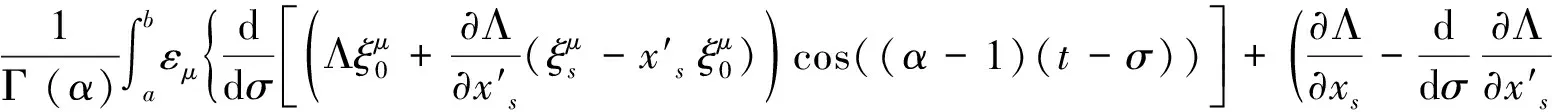
(43)

将方程(13)代入上式，由积分区间的任意性和参数εμ的独立性，得到

(44)

积分后，便得式(42)。证毕。

定理2 对于事件空间中完整非保守系统(13)，如果无限小群变换(17)是基于按周期律拓展的拟分数阶变分问题的Noether准对称变换，则系统存在以下r个线性独立的守恒量

(45)

定理1和定理2可称为事件空间中完整非保守系统基于按周期律拓展的拟分数阶模型的Noether定理。由上述定理，守恒量可由事件空间中完整非保守系统的Noether对称变换或Noether准对称变换求得。

5 事件空间中非完整系统基于按周期律拓展的拟分数阶模型的Noether定理

由于

(46)

将式(46)代入式(15)，考虑到εμ的独立性，得

(47)

即为事件空间中非完整约束(14)对无限小生成函数的限制方程。故有

定理3 对于事件空间中非完整非保守系统(14)(16)，若无限小群变换(17)是基于按周期律拓展的拟分数阶变分问题的Noether准对称变换，且满足限制方程(47)，则系统存在如下r个线性独立的守恒量

(48)

证明由于Noether准对称变换的定义，可得

(49)

或写成形式

(50)

由于满足限制方程(47)，因此有

(51)

将式(51)和式(50)相加，得

(52)

将方程(16)代入式(52)，注意到积分区间的任意性和参数εμ的独立性，得到

(53)

积分之，便得到式(48)。证毕。

定理3可称为事件空间中非完整非保守系统基于按周期律拓展的拟分数阶模型的Noether定理。当没有非完整约束时，则定理3退化为定理2；如果还满足Gμ=0，则定理3退化为定理1。

6 算 例

例1 设非完整非保守系统的Lagrange函数为

(54)

非完整约束为

(55)

在事件空间中，Lagrange函数可表示为

(56)

非完整约束可表示为

(57)

方程(16)的后面两个方程给出

(58)

由方程(57)和(58)可解得

(59)

于是方程(57)给出

(60)

(61)

例2 在平面Kepler问题的Lagrange函数为

(62)

试研究事件空间中该系统基于按周期律拓展的拟分数阶模型的Noether对称性与守恒量。

首先，事件空间中Noether等式(39)给出

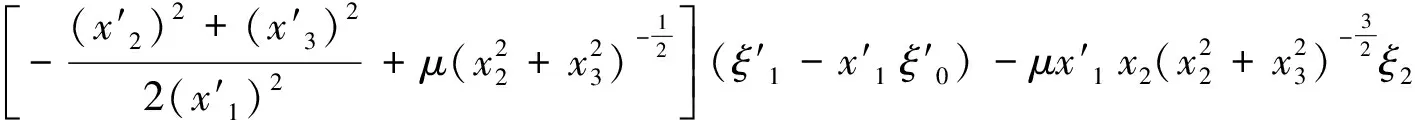
=-G′sec((α-1)(t-σ))

(63)

方程(63)有解

ξ0=0,ξ1=0,ξ2=-x3,ξ3=x2,G=0

(64)

(65)

由判据1，生成元(64)相应于系统的Noether对称变换。由定理1，系统存在如下守恒量

(66)

这是我们基于按周期律拓展的拟分数阶模型得到的由该系统的Noether对称性导致的守恒量。

由判据3，生成元(65)相应于系统的Noether准对称变换。由定理2，守恒量(45)给出。

I=0

(67)

式(67)表明：与生成元(65)相应的守恒量是平庸的。

7 结 论

文章研究了事件空间中完整非保守系统和非完整非保守系统基于按周期律拓展的拟分数阶模型的Noether对称性，建立了相应的Noether定理。文章的主要工作：首先，提出了事件空间中基于按周期律拓展的拟分数阶变分问题，导出了该模型下完整非保守系统和非完整非保守系统的Lagrange方程；其次，给出事件空间中基于按周期律拓展的拟分数阶模型的Noether对称变换与Noether准对称变换的定义和判据；最后，建立并证明了事件空间中完整非保守系统和非完整非保守系统基于按周期律拓展的拟分数阶模型的Noether定理。本文方法可进一步推广应用于研究事件空间中非保守系统的Lie对称性和Mei对称性及其守恒量，也可进一步推广到事件空间中Birkhoff系统等。