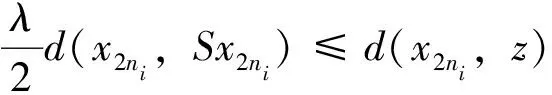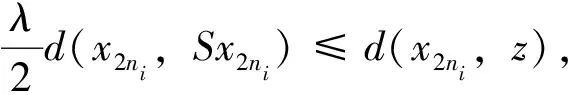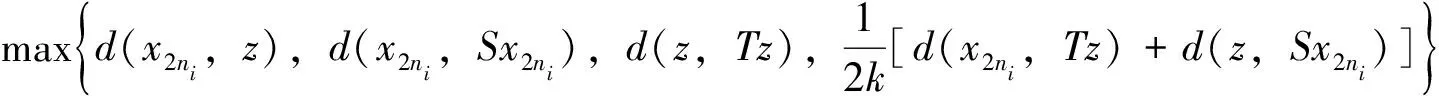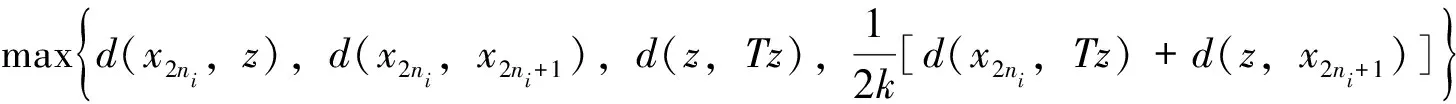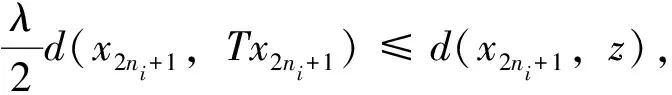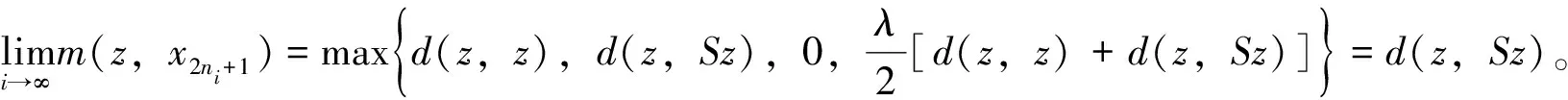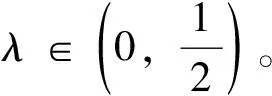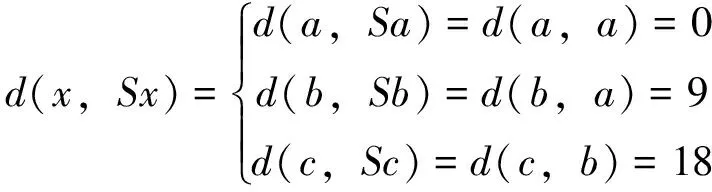推广的Suzuki型(ψ,φ)-弱压缩映射的公共不动点定理

张洁，苏雅拉图

(内蒙古师范大学数学科学学院，内蒙古 呼和浩特 010022)

1 预备知识

定义1[8]设X是非空集合，k≥1是给定的正实数。称函数d:X×X→[0,∞)是X上的b-距离，如果对任意的x,y,z∈X, 满足

(i)d(x,y)=0当且仅当x=y;

(ii)d(x,y)=d(y,x);

(iii)d(x,y)≤k(d(x,z)+d(z,y))。

此时，称(X,d)为b-距离空间。

例1[9]设X=(0,∞)，定义

则(X,d)是k=2的b-距离空间。

定义2[8]设(X,d)是b-距离空间。

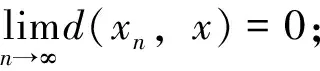
(ii)称序列{xn}是Cauchy列，如果序列{xn}满足，对于任意ε>0, 存在正整数N, 当m,n>N时，d(xm,xn)<ε；

(iii)称(X,d)是完备的，如果(X,d)中每一个Cauchy列都收敛。

本文假设b-距离是连续的。

2 主要结果

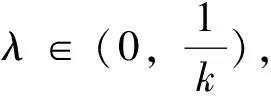
能推出

ψ(d(Sx,Ty))≤(1-λ)ψ(m(x,y))-λφ(m(x,y))

(1)

其中

(i)ψ:[0,∞)→[0,∞)是单调递增的连续函数，且ψ(t)=0当且仅当t=0；

(ii)φ:[0,∞)→[0,∞)是下半连续函数，且φ(t)=0当且仅当t=0；

则S和T有唯一的公共不动点。

证明设x0∈X。 构造X中的序列{xn}, 使得x2n-1=Sx2n-2,x2n=Tx2n-1,n=1,2,。下面总假设对每一个n∈N,xn≠xn+1。 如若不然，公共不动点必然存在。

事实上，如果存在n∈N, 使得x2n=x2n-1。下面证明x2n-1是S和T的公共不动点。 因为

故由不等式(1)得

ψ(d(Sx2n,Tx2n-1))≤(1-λ)ψ(m(x2n,x2n-1))-λφ(m(x2n,x2n-1))

其中

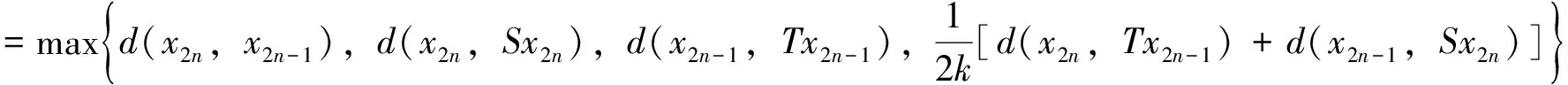
=d(x2n-1,Sx2n)

因此

ψ(d(Sx2n,x2n-1))=ψ(d(Sx2n,x2n))=ψ(d(Sx2n,Tx2n-1))

≤(1-λ)ψ(d(x2n-1,Sx2n))-λφ(d(x2n-1,Sx2n))

从而

λψ(d(Sx2n,x2n-1))≤-λφ(d(x2n-1,Sx2n))

由函数ψ的定义知ψ(d(Sx2n,x2n-1))≥0,于是由上面的不等式知 -φ(d(x2n-1,Sx2n))≥0,即φ(d(x2n-1,Sx2n))≤0,再由函数φ的性质得φ(d(x2n-1,Sx2n))=0,因此x2n-1=Sx2n。这时，Sx2n-1=Sx2n=x2n-1=x2n=Tx2n-1，即x2n-1是S和T的公共不动点。类似地，如果存在n∈N, 使得x2n-1=x2n-2, 则x2n-2是S和T的公共不动点。

第1步证明

(2)

和

(3)

对每一个n∈N,

由不等式(1)得

ψ(d(Sx2n,Tx2n-1))≤(1-λ)ψ(m(x2n,x2n-1))-λφ(m(x2n,x2n-1))

(4)

其中

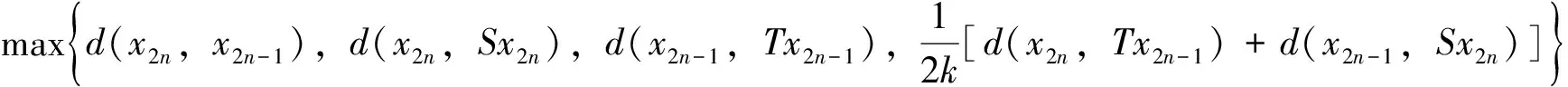
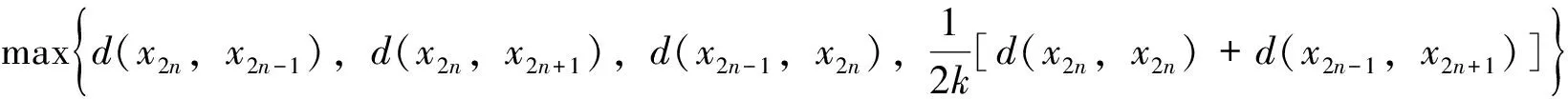
若m(x2n,x2n-1)=d(x2n,x2n+1), 则由不等式(4)得

ψ(d(x2n,x2n+1))≤(1-λ)ψ(d(x2n,x2n+1))-λφ(d(x2n,x2n+1))

进而可推出φ(d(x2n,x2n-1))=0,即x2n=x2n-1, 这与x2n≠x2n-1相矛盾。

因此

上述事实说明m(x2n,x2n-1)=d(x2n,x2n-1), 于是由不等式(4)得

ψ(d(x2n,x2n+1))≤(1-λ)ψ(d(x2n,x2n-1))-λφ(d(x2n,x2n-1))

(5)

类似地，

ψ(d(x2n+1,x2n+2))≤(1-λ)ψ(d(x2n,x2n+1))-λφ(d(x2n,x2n+1))

(6)

结合不等式(5)-(6)得，对所有的n∈N,

ψ(d(xn+1,xn))≤(1-λ)ψ(d(xn,xn-1))-λφ(d(xn,xn-1))

(7)

由于φ(d(x2n,x2n-1))≥0, 故

ψ(d(xn+1,xn))≤(1-λ)ψ(d(xn,xn-1))<ψ(d(xn,xn-1))

再由ψ函数的性质得

0≤d(xn+1,xn)≤d(xn,xn-1)

这说明{d(xn+1,xn)}是单调递减有下界的数列，故存在一个实数r, 使得

下证r=0。

事实上，对不等式(7)两端取极限得

ψ(r)≤(1-λ)ψ(r)-λφ(r)

因此φ(r)≤0, 于是得r=0, 即式(2)成立。 由三角不等式得。

d(xn,xn+2)≤kd(xn,xn+1)+kd(xn+1,xn+2)

第2步证明{xn}是Cauchy列。

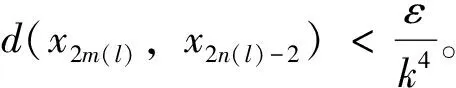
由三角不等式知

ε≤d(x2m(l),x2n(l))≤kd(x2m(l),x2n(l)-2)+kd(x2n(l)-2,x2n(l))

注意到式(3)，并对上面不等式两端取极限得

再利用三角不等式得

ε≤d(x2m(l),x2n(l))≤kd(x2m(l),x2m(l)-1)+kd(x2m(l)-1,x2n(l))

(8)

d(x2m(l)-1,x2n(l))≤kd(x2m(l)-1,x2n(l)-2)+kd(x2n(l)-2,x2n(l))

≤k2d(x2m(l)-1,x2m(l))+k2d(x2m(l),x2n(l)-2)+kd(x2n(l)-2,x2n(l))

(9)

注意到式(2)-(3)，并对不等式(8)-(9)两端取极限得

同理得

类似地,

ε≤d(x2m(l),x2n(l))≤kd(x2m(l),x2m(l)-1)+kd(x2m(l)-1,x2n(l))

≤kd(x2m(l),x2m(l)-1)+k2d(x2m(l)-1,x2n(l)+1)+k2d(x2n(l)+1,x2n(l)),d(x2m(l)-1,x2n(l)+1)

≤kd(x2m(l)-1,x2n(l)-2)+kd(x2n(l)-2,x2n(l)+1)

≤k2d(x2m(l)-1,x2m(l))+k2d(x2m(l),x2n(l)-2)+k2d(x2n(l)-2,x2n(l))+k2d(x2n(l),x2n(l)+1)

对上面两个不等式两端取极限得

由式(2)知，对充分大的l和上述的ε>0,有

进而有

ε≤d(x2m(l),x2n(l))

≤kd(x2m(l),x2m(l)-1)+kd(x2m(l)-1,x2n(l))

即

这时有

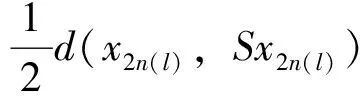
令x=x2n(l),y=x2m(l)-1,将其代入不等式(1)得

ψ(d(x2n(l)+1,x2m(l)))=ψ(d(Sx2n(l),Tx2m(l)-1))

≤(1-λ)ψ(m(x2n(l),x2m(l)-1))-λφ(m(x2n(l),x2m(l)-1))

(10)

其中

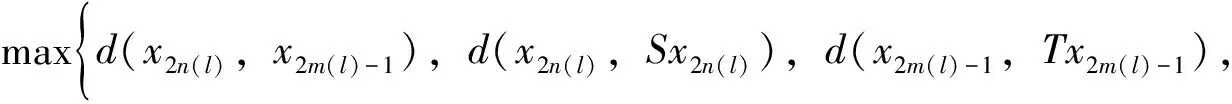
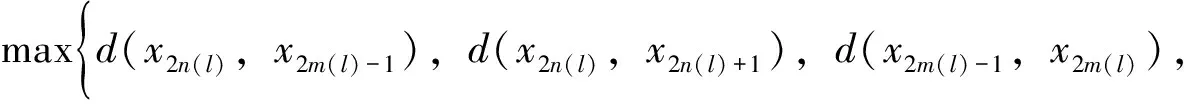
因而

对不等式(10)两端同时取极限得

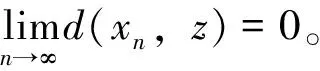
第3步要证z是T和S的公共不动点。先证

中必有一个不等式成立。 否则,

d(x2n,x2n+1)≤kd(x2n,z)+kd(z,x2n+1)

=kλd(x2n,x2n+1)

于是d(x2n,x2n+1)=0,推出x2n=x2n+1,这与x2n≠x2n+1相矛盾。 因此存在{ni}使

ψ(d(x2ni+1,Tz))=ψ(d(Sx2ni,Tz))≤(1-λ)ψ(m(x2ni,z))-λφ(m(x2ni,z))

(11)

其中

因而

再对不等式(11)两端取极限得

ψ(d(z,Tz))≤(1-λ)ψ(d(z,Tz))-λφ(d(z,Tz))

从而有φ(d(z,Tz))=0, 即z=Tz。由

和不等式(1)得

ψ(d(Sz,z))=ψ(d(Sz,Tz))≤(1-λ)ψ(m(z,z))-λφ(m(z,z))

=(1-λ)ψ(d(z,Sz))-λφ(d(z,Sz))

从而d(z,Sz)=0, 即z=Sz。因此z是T和S的公共不动点。

ψ(d(x2ni+2,Sz))=ψ(d(Sz,Tx2ni+1))≤(1-λ)ψ(m(z,x2ni+1))-λφ(m(z,x2ni+1))

(12)

其中

类似情形1的证明，得到Tz=Sz=z。

第4步证明公共不动点的唯一性。

假设y是T和S的公共不动点，由于

因而

ψ(d(y,z))=ψ(d(Sy,Tz))≤(1-λ)ψ(m(y,z))-λφ(m(y,z))

=(1-λ)ψ(d(y,z))-λφ(d(y,z))

进而推出d(y,z)=0,即y=z。

下面给出一个例子。

设X={(1,1),(4,1),(1,4)}。定义

d(x,y)=|x1-y1|2+|x2-y2|2

令a=(1,1),b=(4,1),c=(1,4),则d(a,b)=9,d(a,c)=9,d(b,c)=18。

定义S:X→X为Sa=a,Sb=a,Sc=b;T:X→X为Ta=a,Tb=a,Tc=a,则

令ψ(t)=t,φ(t)=1-e-t,0∈[0,+∞)。这时

ψ(d(Sx,Ty))≤(1-λ)ψ(m(x,y))-λφ(m(x,y))

(i)当x=a,y=b时，

ψ(d(Sa,Tb))=ψ(d(a,a))=ψ(0)=0,

(1-λ)ψ(m(x,y))-λφ(m(x,y))=(1-λ)ψ(9)-λφ(9)

=9(1-λ)-λ(1-e-9)

=9-λ(9+1-e-9)

>0

因此ψ(d(Sx,Ty))≤(1-λ)ψ(m(x,y))-λφ(m(x,y))成立。

(ii)当x=b,y=c时，

ψ(d(Sb,Tc))=ψ(d(a,a))=ψ(0)=0,

(1-λ)ψ(m(x,y))-λφ(m(x,y))=(1-λ)ψ(18)-λφ(18)

=18(1-λ)-λ(1-e-18)

=18-λ(19-e-18)

>0

因此ψ(d(Sx,Ty))≤(1-λ)ψ(m(x,y))-λφ(m(x,y))成立。

(iii)当x=a,y=c或x=b,y=a时，与(i)的情形完全相同。

(iv)当x=c,y=b时，与(ii)的情形完全相同。

综合情形(i)～(iv)可知，定理1 的条件被满足。 由定理1 可知，S和T存在公共不动点，且公共不动点为(1,1)。