华南地区花岗岩残积土粗颗粒定量化的形态表征

徐长文 ，刘锋涛,2，张澄博，高燕

(1.中山大学地球科学与工程学院，广东 珠海 519000;2.广东省地球动力作用与地质灾害重点实验室，广东 广州 510275)

花岗岩残积土是我国华南地区工程建设中常见的岩土体之一，此类土体是在花岗岩母岩受到亚热带高温、湿润多雨气候影响，经长期物理风化作用、化学风化作用、生物风化作用风化分解后堆积而形成的。原岩中的长石、云母、角闪石风化成伊利石、蒙脱石、绿泥石等粘土矿物[1]，而石英矿物残留，成为花岗岩残积土中粗颗粒(以下简称粗粒)的主要组成。花岗岩残积土中粗细粒含量与岩土体受到的风化程度有关，而且各个粒径区间颗粒的形态特征也存在差异，可见花岗岩残积土是一种粗细粒混合的特殊性土。由于粗细粒土颗粒具有不同的形态特征、物理力学特性，受到内部和外部压力时表现也不同，导致了花岗岩残积土的非均质性和各向异性，因此研究花岗岩残积土中粗粒的形态、空间分布等细观、微观结构特征对其工程应用具有重要的意义[2-3]。已有研究表明土颗粒的形状对土体的力学性质有显著的影响，如不同粒径的颗粒形状具有不同的球度、圆度和平滑度，颗粒越不规则，砂土的最大孔隙比和最小孔隙比越大[4]；增加颗粒的伸长率，粗细混合砂土剪切破坏时的内摩擦角也增大，增大颗粒的平滑度，剪切破坏时的内摩擦随之减小[5]；长条形颗粒间具有更强的咬合力，比各向同性的颗粒表现出更大的抗剪强度[6]，因此在建立土体本构模型，特别是离散元数值模型中必须要合理的考虑土体中粗粒的几何形态特征。然而自然界中土颗粒真实的几何形态是不规则的，且千差万别杂乱无章，其特征规律似乎毫无规律可循。因此精准获取土体中所有土颗粒的真实几何形态是难以实现的，这是目前研究不规则颗粒对土体力学性质影响的主要难题之一。尤其是华南地区花岗岩残积土受风化条件影响，搬运距离较短或未经历搬运过程，粗粒含量较高且几何形态复杂，因此科学合理的表征其中粗粒几何形态成为准确描述华南地区花岗岩残积土工程力学性质的关键。

Barrett[7]结合地质因素总结3个主要的无量纲参数来描述土颗粒的几何形态，轮廓形状、圆度和表面纹理。其中轮廓形状指颗粒的整体形状，多为由颗粒的三轴比所测相关系数的无量纲组合，如扁平度(最短轴与最长轴之比)、球度(颗粒体积与最小外接球体积之比)[8]、伸长率(中间轴长与最长轴之比)等；圆度反应颗粒棱角的磨圆程度，与风化搬运距离有关，用棱角曲率半径与最大内切球半径之比的均值表示[8]，但是对于曲率的选取和棱角的定义具有人为因素的偏差，Ferellec等[9]用颗粒投影轮廓上所有内切圆的平均半径代替棱角平均曲率半径，提高了该参数的重现性；表面纹理反应颗粒表面的细微形态，用来描述颗粒表面和棱角微观尺度的粗糙度[10]，也能体现地质作用对岩石块体颗粒的影响，如擦痕、雨痕。此外前人还进一步提出了不同的二维形状参数，包括圆度系数(4π×投影面积/投影周长的平方)、形状系数和棱角系数[10]、以及形状参数(将风化花岗岩中石英、长石、黑云母等矿物颗粒投影轮廓简化为四边形)[11]等，这些参数都是在垂直投影二维平面内统计分析颗粒形态，张家发等[12]等通过特制夹具对比研究了不同旋转角度下碎石颗粒的形态特征，避免了单一角度测定的人为影响。上述文献中各种不同定义和意义的形状因子都是一种与颗粒形态有关的无量纲值，在一定程度上能表征颗粒形状对标准形状(二维平面取圆形)的偏离，需根据研究对象的相关信息选用合适的形状因子。

不规则土颗粒几何形态参数的分析方法较为常用的有分形理论法和FFT(快速傅立叶变换法)。基于分形理论[13]，Kennedy等[14]构造多边形近似表示颗粒形状，发现多边形的边的数量与周长P成正比，与步长S(边长)成反比。这种关系在双对数坐标logP-logS中呈线性，斜率表示颗粒的不规则性，斜率越高颗粒越不规则。文献[15]中研究表明，尖棱角状颗粒投影轮廓线凹凸较多，分维也较大；次棱角状颗粒投影轮廓比较平滑，分维较小。因此分维能够定量描述不规则颗粒形态有自相似性的圆度和表面纹理，但描述颗粒的整体形状时仅使用分维值存在偏差，还需结合其他形状参数描述，而且通过分维值也很难重构相似特征的颗粒形状。随着数字图像技术的发展，Fourier分析法因其可靠和高效性成为一种精确定量描述和重构颗粒形态特征的新方法。Ehrlich等[16]最早以Fourier级数展开的方式定量描述颗粒的二维轮廓，正余弦函数总数N越大，对颗粒形状的描述越精确，但所需的运算量N2也相应增大，大批量处理颗粒轮廓较为困难。后来Meloy[17]使用快速傅里叶变换(FFT)方法极大的提高了计算效率，运算量仅为Nlog2N，能够快速统计分析大量颗粒轮廓，而且通过FFT得到的幅度值和相位角能够精确重构出颗粒的原始轮廓，通过改变相位角还可以生成具有相似形态特征的任意颗粒形状，进行离散元数值模拟时具有统计意义，这使得Fourier分析法在颗粒轮廓定量化表征方面的研究得到越来越多的应用[18-23]。

本文将结合显微光学成像、数字图像处理方法获取4个粒径区间各1 000个粗颗粒的二维最大投影轮廓，并通过FFT求得这些粗粒轮廓的平均幅度值，从统计意义上研究粗粒的几何形态特征，分析讨论了华南地区花岗岩残积土粗粒Fourier描述子与粒径之间的关系，并与滨海冲积石英砂、黄河中游冲积河砂中粗粒的Fourier描述子进行了对比分析，为研究花岗岩残积土本构关系，特别是建立花岗岩残积土的离散元数值模型奠定基础。

1 颗粒几何形态的定量化表征

1.1 试验样品

试验所用花岗岩残积土取自深圳市龙华新区，呈浅肉红、褐黄色，为燕山晚期中—粗粒花岗岩经长期风化作用残积而成。扰动后的花岗岩残积土较为松散，颗粒间易粘结成团状，需经烘干、碾碎处理。按照《土工试验方法标准》(GB/T 50123-1999)[24]筛析法试验规范要求，烘干至恒重后测得颗粒级配曲线(见图1)，其余物理指标中天然含水量为26.8%，天然密度为1.765 g/cm3，相对密度为2.58，天然孔隙比为0.85，有效粒径为0.078 mm，中值粒径为1.424 mm，不均匀系数为29.69，曲率系数为1.38。土样过0.5 mm分析筛，取筛后余土测液塑限，测得塑性指数为16.8，液性指数为0.21。根据国家标准《土的工程分类标准》(GB/T50145-2007)[25]，试验取得的花岗岩残积土中粒径小于0.075 mm的颗粒含量占总质量的10.9%，0.075～2 mm的颗粒占56.5%，属于含细粒土砂。花岗岩残积土为华南地区典型的风化原位土，粗粒主要成分为石英和少量岩屑，为了对比不同矿物组成的颗粒与石英颗粒受到不同风化作用后几何形态特征的规律，本文还选取了黄河中游的冲积河砂，广东滨海冲积石英砂。其中黄河冲积砂土中各粒径区间粗粒矿物组成差别较大，粒径较小的粗粒中主要为石英矿物，粒径较大的粗粒多为岩石碎屑，矿物组成主要为角闪石、赤铁矿、绿帘石等[26]，滨海冲积石英砂(简称为海砂)中粗粒主要矿物组成为石英。

为了统计分析花岗岩残积土和冲积河砂、海砂中各粒径区间粗粒的几何形态特征，增大样本容量，本文将土样分为0.5～1、1～2、2～5 和5～10 mm共4组，每组各随机取1 000个颗粒进行测试，降低了离散性样本对试验结果的影响，测试样品见图2。

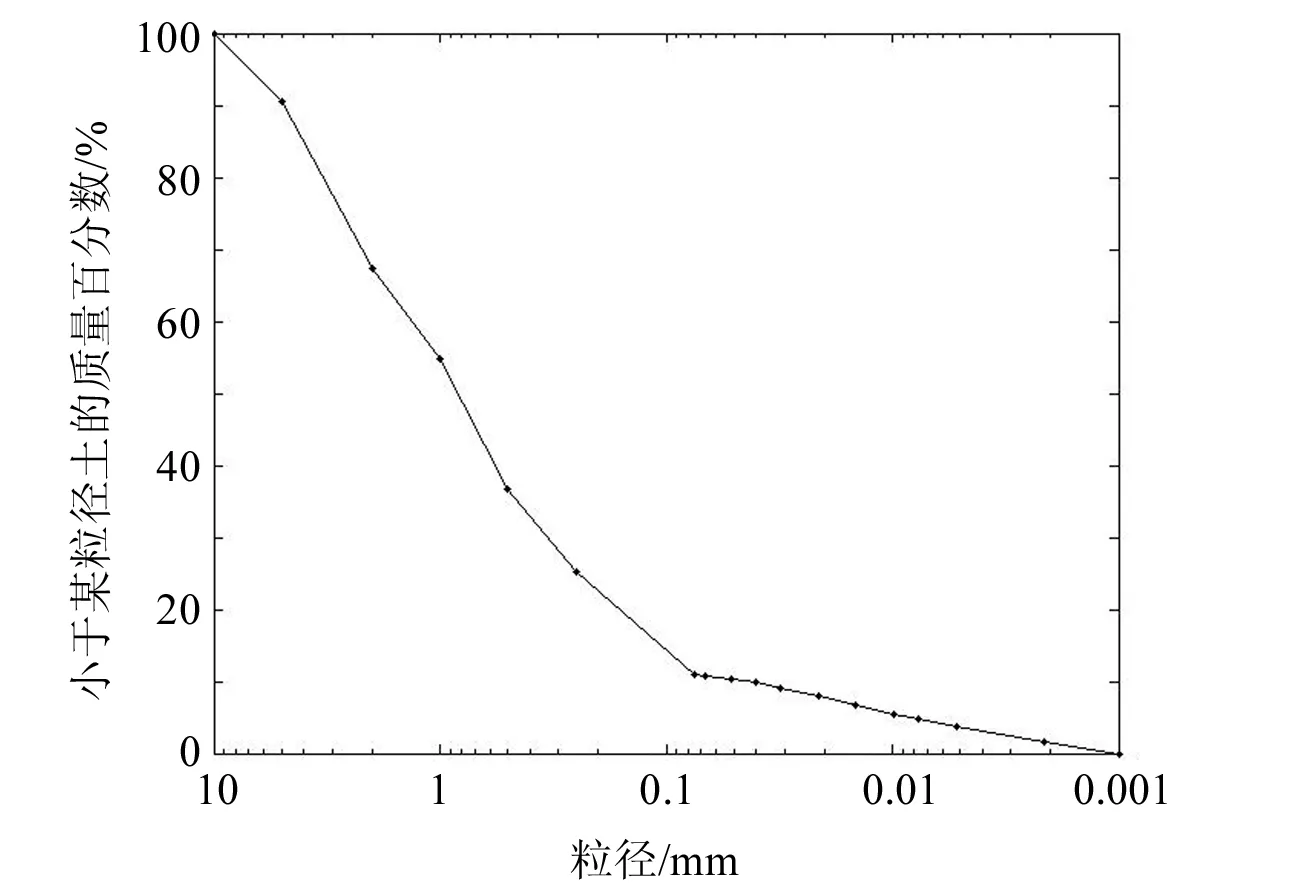
图1 花岗岩残积土的颗粒级配曲线Fig.1 The grain size distribution curve of residual granite soil

图2 土颗粒样品Fig.2 Soil particle sample

1.2 颗粒二维图像处理

本文通过基恩士超景深三维显微系统VHX-5 000垂直拍摄获取上述4个粒组粗粒的二维图像，分辨率为1 600×1 200，放大倍率为20。为了尽可能的体现粗粒的整体形态，减少光照等因素的影响，使用透光拍摄且每个粗粒均为最大投影面积。获得的图像在MATLAB软件中进行处理并获取粗粒轮廓边界。首先将图像转化为256位的灰度图像，由于拍摄时光线环境的变化和粗粒表面的反光会对图像产生一些噪声，在经过对比多个滤波器处理后选择效果最好的中值滤波器进行去噪处理，在去噪的同时能很好得保留粗粒轮廓的边缘细节。其次，选择合适的阈值将灰度图像二值化，这样能减少图像中的数据量，凸显出粗粒的轮廓边界。然后对二值图像进行腐蚀、膨胀、开运算、闭运算、孔洞填充等形态学图像处理，得到基本符合粗粒真实轮廓的二值图像。最后通过边界提取算法得到粗粒的边界坐标，花岗岩残积土和黄河中游冲积河砂的粗粒图像见图3，滨海冲积石英砂粗粒的图像处理方式与之一致。以上图像处理过程均在MATLAB软件中编写相应代码自动实现。

在计算机中数字图像是由像素的矩阵表示的，反应图像的亮暗差别。每个像素都有整数行和列的位置坐标，因此在二值图像中得到的颗粒轮廓边界是由一个个离散的像素点构成的，不同的是，像素坐标中坐标原点位于图像的左上角。通过图像中的标尺计算得到1 mm等于91个像素间距，因此从颗粒轮廓边界的像素坐标可得到对应的实际边界物理坐标，反应花岗岩残积土中粗颗粒的真实投影形状，为下一步使用Fourier分析法定量描述颗粒轮廓特征奠定基础。从图3(a1-d1)中可以看出花岗岩残积土中粗粒主要是石英颗粒，不同粒径区间的不规则形状具有较强的相似性，棱角性、表面粗糙度等不规则特征较为明显。与此不同的是，图3(a2-d2)中不同粒径的黄河冲积砂的矿物类型、不规则程度存在明显的差异，小粒径颗粒中多为石英颗粒，随着粒径增大石英颗粒的含量逐渐减少，而且石英颗粒的不规则特征变化不大都表现出表面粗糙的特点。但其他矿物组成的颗粒则不规则程度变小，表面越来越光滑。综上所述，无论是花岗岩残积土还是冲积砂土中的石英颗粒的表面粗糙程度受到搬运风化的影响较小。为了定量的表征上述粗粒几何形态特征，下文中在数字图像处理后提取试样颗粒的轮廓线，并采用FFT的方法分析其特征规律。

图3 颗粒图像处理过程Fig.3 Image processing of particles

1.3 傅里叶描述子定量描述颗粒轮廓形态

根据傅里叶变换理论，任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示。颗粒轮廓也可作为周期函数，需要在二维平面中，将颗粒轮廓基于一点展开，进行周期延拓。首先在颗粒轮廓边界内选择一中心点O，以等角度间隔θp(2π/Np)计算中心点至边界的半径距离Rk=OPk，颗粒轮廓就能由Np个周期为2π的离散点Pk表示[16, 18]，见图4。然后对周期离散信号Rk(θk)进行Fourier级数展开，取一个周期即为离散傅里叶变换(DFT)，公式如下：

(1)

(2)

式中，Rk(θk)为角度θk对应的半径Rk，N为正弦或余弦函数的总数，n是调和数，An和Bn为Fourier系数，分别表示余弦分量和正弦分量所对应的幅度值，R0为颗粒的平均半径，An和Bn为0时，颗粒轮廓是半径为R0的圆。

因为颗粒轮廓是由Np个离散点构成的，An和Bn可通过以下公式求出：

(3)

(4)

离散傅里叶变换DFT在本文中通过快速傅里叶变换算法FFT实现，提高了大批量处理颗粒轮廓的运算速度。

图4 颗粒轮廓傅里叶变换Fig.4 Fourier transform on particle boundary

在傅里叶变换时，用N个正弦函数和余弦函数的叠加来拟合Rk(θk)，只要N≥Np就可以精确重构颗粒的轮廓信息，而且为了方便进行FFT运算取N为2的整数次方，文中N=Np= 128，在减少计算量的同时又能保证颗粒重构精度。

为了更好的体现颗粒轮廓形态特征在频率域中的规律性，对于具有相似特征的颗粒，Bowman[18]、Mollon和Zhao[21]使用归一化的幅度值来统一描述颗粒形态的相关特征，公式为

(5)

式中，Dn称为Fourier描述子，D0=1。

本文统计分析了华南地区花岗岩残积土中4个粒径区间的粗颗粒，通过Fourier描述子Dn即可在频率域定量化描述各粒径区间具有相似形态特征的颗粒轮廓，并与冲积河砂、海砂中相同粒组粗颗粒的Fourier描述子Dn进行了对比分析，下文详细讨论分析结果。

2 分析和讨论

颗粒的几何形态特征在很大程度上影响其空间排列、颗粒间摩擦性能、裂隙破坏方式等细微观结构特性，而华南地区花岗岩残积土由于风化程度不同，粗细粒含量相差较大，因此分析其粗粒几何形态特征与粒径之间的关系尤为重要。而且花岗岩残积土多属于风化沉积的原位土，其中粗粒与经历长期风化搬运作用的冲积砂土中粗粒的几何形态特征存在着一定差别，通过Fourier描述子可将这种差异定量表示。

图6 颗粒归一化平均幅度频谱图Fig.6 Normalized mean amplitude spectra of particles

表1为3种粗颗粒4个粒径区间的Fourier描述子特征Dn值(2 ≤n≤ 8)。从表1和图6可知，3种粗粒中粒径5～10 mm粗粒的D2～D8均最小，0.5～1 mm粗粒的D2最大，表明5～10 mm粗粒的平均伸长率和棱角度最小，0.5～1 mm粗粒的平均伸长率最大，即无论是残积土还是冲积土，其粗粒的粒径越大，颗粒的规则程度越高，相反粒径越小，长条形颗粒越多，棱角度越大。对于花岗岩残积土，0.5～10 mm之间的4个粒组粗粒D3-D8值均相差不大，表明这3个粒径区间粗粒的表面粗糙程度基本相近，这与其未经历过长期的搬运作用有关，为研究华南地区花岗岩残积土的风化过程提供参考价值。

与冲积相海砂的各粒组粗粒的Dn值对比发现，花岗岩残积土四个粒径区间中粗粒的伸长率、棱角度等特征均较小，说明海砂粗粒中长条形颗粒含量较原位花岗岩残积土高，颗粒的不规则度也较大。由于海砂和花岗岩残积土粗粒中石英含量均较高，这表明经历过海水长期的冲刷搬运作用后，海砂中石英颗粒发生断裂破碎，棱角性增强，伸长率变高，与原位残积土存在一定差异，但表面粗糙程度等微观形态基本不变。与冲积河砂相比，花岗岩残积土中粗粒的伸长率、棱角度等形态参数较大，这是由于河砂中粗粒受物源影响，成分较为复杂，受风化作用影响，1～10 mm粗粒多为岩屑碎块，矿物组成以角闪石、绿帘石为主，经历长期的搬运作用后，粗粒的磨圆度较高，形状较规则，而0.5～1 mm粗粒中石英含量明显增加，抗风化能力变强，颗粒的棱角度等形态参数与花岗岩残积土相差不大，这表明风化作用对不同粒径、不同矿物颗粒形状的影响也是不同的。

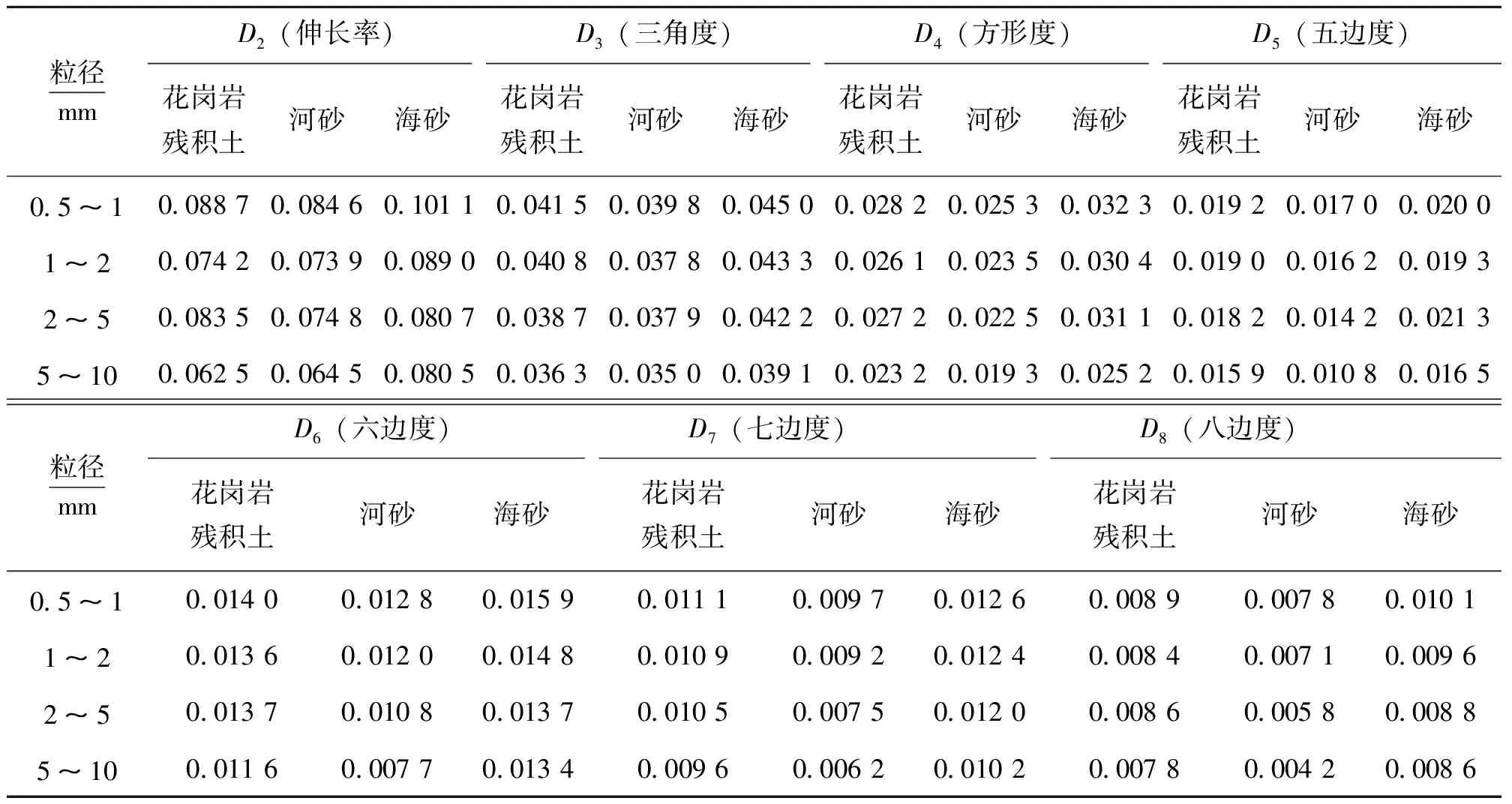
表1 四个粒径区间粗粒的平均Dn值Table1 Average Dn of coarse grain of four particle size intervals

Meloy[17]发现，幅度与频率序列(n> 8)在双对数坐标log2Cn-log2n中呈线性关系，并且颗粒表面粗糙度可由直线的斜率和纵轴截距定量描述。截距大表示颗粒表面粗糙度高，斜率表示颗粒轮廓从细观到微观表面粗糙度的变化，直线越陡，微观尺度下颗粒表面越光滑[18]。本文根据试验所用花岗岩残积土，统计分析4个粒组各1 000个粗粒在log2Dn-log2n坐标中的关系，并与冲积河砂、海砂进行了对比(见图7)。

试验结果表明，4个粒组粗粒的Fourier描述子Dn与频率序列n均呈线性关系，可由方程log2Dn-log2D2=a(log2n-1)表示，即

Dn=2alog2n+log2D2-a，n≥ 2

(6)

其中，a为线性方程的斜率，4个粒组粗粒对应的线性方程见表2。

图7 Fourier描述子与频率序列关系图Fig.7 The relationship between Fourier descriptors and frequency sequence

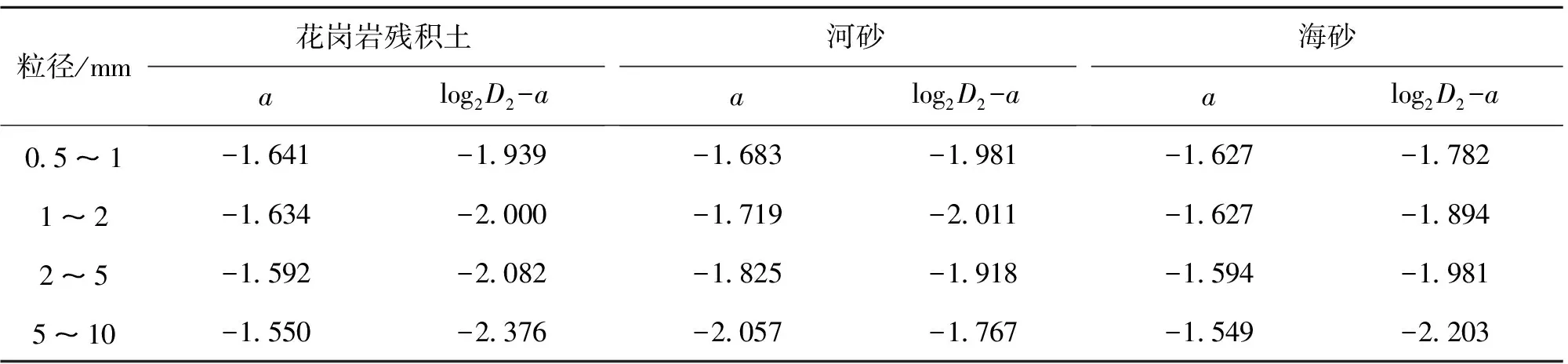
粒径/mm花岗岩残积土alog2D2-a河砂alog2D2-a海砂alog2D2-a0.5～1-1.641-1.939-1.683-1.981-1.627-1.7821～2-1.634-2.000-1.719-2.011-1.627-1.8942～5-1.592-2.082-1.825-1.918-1.594-1.9815～10-1.550-2.376-2.057-1.767-1.549-2.203

由表2可知，花岗岩残积土中0.5～10 mm粗粒的Dn值与频率序列n在双对数坐标中的截距基本相同，表明这四个粒径区间颗粒的表面粗糙程度等微观形态特征基本一致。河砂粗粒的斜率最小，表明该类粗粒表面光滑度较高，与河砂中鹅卵石形态颗粒较多有关，以大于5 mm的粗粒中最多。通过比较花岗岩残积土和海砂中粗粒的线性方程发现，二者的斜率非常接近，说明两种粗粒的微观特征也非常相似，这可能与二者粗粒中石英含量较高有关。最后通过斜率a、D2两个参数就可求出频率域内包含粗粒轮廓所有几何形态信息的Fourier描述子Dn，从而在统计意义上定量描述华南地区花岗岩残积土中各粒径区间粗粒的形态特征，为研究粗粒形态对土体力学性质的影响和离散元法建模提供先决条件。

3 结 论

土颗粒的几何形态对土体的工程力学性质有显著的影响，尤其是华南地区花岗岩残积土中粗粒含量较高，科学合理地表征粗粒的几何形态特征对准确描述花岗岩残积土工程力学性质具有重要意义。为此，本文以定量化表征华南地区花岗岩残积土中粗粒几何形态为基础，通过分析四个粒径区间大量粗粒的最大投影轮廓，运用FFT法计算得到各粒组包含粗粒轮廓的Fourier描述子Dn，获取了对华南地区花岗岩残积土粗粒几何形态定量化指标的统计规律，并且与黄河中游冲积河砂、滨海冲积石英砂的粗粒形态特征进行了对比。研究结果表明：

1)在3种粗粒的4个粒径区间中，0.5～1 mm粗粒的平均伸长率最大，5～10 mm粗粒的平均伸长率和棱角度最小，即无论是残积土或者冲积土，粗粒粒径越大，颗粒的规则程度越高；粒径越小，颗粒的伸长率越大，棱角度越高。

2)花岗岩残积土中0.5～10 mm之间的4个粒径区间粗粒的表面粗糙程度等细微观特征基本相近，与其未经历过长期的搬运作用有关。

3)冲积河砂中粒径较大粗粒多为岩石碎屑，矿物组成以角闪石、绿帘石为主，Dn(n>8)值较低，说明其在搬运过程中被磨圆，降低了表面粗糙程度，而0.5～1 mm粒组的Dn(n>8)值与花岗岩残积土各粒组的基本相同，表面粗糙程度都较高，这与二者粗粒中石英含量较高有关，说明石英颗粒在搬运过程中会发生断裂破坏从大颗粒破碎为小颗粒，但其表面不会被磨圆，而且土颗粒的几何形态特征受到了颗粒矿物组成的影响。

4)运用Fourier分析法只需斜率a、D2两个参数就可求出频率域内包含颗粒轮廓所有形态信息的Fourier描述子Dn，而且改变相位角φn还可随机生成具有相似形态特征的颗粒轮廓，对土颗粒建模具有重要作用。

本文仅研究了花岗岩残积土中粗粒的二维最大投影几何形态特征，接下来需要进一步研究如何高效快速的获取大量粗粒的三维几何形貌的实验方法，和开发相应的数字图像处理技术以及Fourier分析方法，并深入进行粗粒的三维形貌重构等相关研究。此外，若全面分析华南地区花岗岩残积土中粗粒的空间形态特征，仍需对不同地质成因、不同风化条件下的花岗岩残积土以及更多粒径区间颗粒(尤其是较细颗粒)进行深入的研究。