非正交多址接入无线供电通信网络的能量传输开启条件研究

曾志超，崔苗，林凡，张磊，胡涵飞，张广驰

(1.广东工业大学信息工程学院，广东 广州 510006；2. 广州杰赛科技股份有限公司，广东 广州 510310；3. 中国电子科技集团公司第五十四研究所，河北 石家庄 050081；4. 中国电子科技集团公司第七研究所，广东 广州 510310)

受到未来无线通信网络流量爆炸性增长以及网络用户激增的影响，下一代移动通信网络需要更为灵活的接入技术以更好地支持大规模连接。最近，非正交多址接入(non-orthogonal multiple access，NOMA)因其较高的频谱效率和较好的用户公平性，受到越来越多学者的关注[1-9]。NOMA已经被认为是5G移动通信系统中最有前景的技术[3-4]。非正交多址接入的基本思想是利用功率域的多路复用使得用户可以访问相同的时频资源；在接收机处，使用串行干扰消除(successive interference cancellation，SIC)来解码不同用户信号。虽然使用串行干扰消除增加了接收机解码的复杂度，但却大大提高了系统的吞吐量[3,5]。在文献[6]中，作者研究了随机部署用户的下行链路非正交多址接入方案的性能；在文献[7]中，作者将非正交多址接入应用于协作通信网络的下行链路。基于非正交多址接入的鲁棒资源分配问题也有相应的研究[8]。为了降低串行干扰消除的复杂度，文献[9]提出了使用非正交多址接入和时分多址接入混合组网的方式，并认为最大化网络吞吐量和保证用户簇的公平性是一对矛盾的问题。

网络节点先收集能量，然后利用收集到的能量传输信息的网络通常称为无线供电网络(wireless powered communication networks，WPCN)[8-12]。无线供电通信网络通常由1个基站和N个能量收集用户组成，前者通过下行链路广播无线射频能量，后者通过上行链路传输信息，这就是所说的基于“先收集能，然后再传输信息”协议的无线供电通信网络[8-12]。文献[10]中是最典型的基于“先收集能，然后再传输信息”协议的无线供电通信网络，它使用时分多址(TDMA)接入方式，其帧被划分为N+1个子区间; 一个用于下行能量传输，剩下N个用于信息传输的N个用户。丁志国团队将它扩展到非正交多址接入场景[11]，与文献[10]不同的是：使用非正交多址接入可以提高系统的吞吐量；在衰落信道中，还可以动态调整子区间的时间分配来最大限度地提高无线供电通信网络上行链路的和速率[8-9]。然而，文献[10-11]中的资源分配策略对小区边缘用户是不公平的，因为会产生双远近效应问题。这种效应依赖于距离的大尺度衰落，即距离基站较远的用户接收到的无线能量要比距离较近的用户要少得多，但距离较远的用户必须以更高的功率传输，才能达到与距离较近的用户相同的速率。另外，无线携能传输(simultaneous wireless information and power transfer，SWIPT)作为无线能量传输技术的一种也有不少研究者做了相应的研究[13-16]。

然而，对于非正交多址接入的无线供电通信网络系统来说，在无线能量传输阶段需要专门的时间和频率资源，会有大量的损耗，这种损耗对于设备数量庞大的物联网来说是不可行的，也不符合未来5G通信网络追求绿色通信的愿景。物联网设备一方面可以通过下行无线能量传输获取能量，另一方面可从可再生能源或环境中的射频信号获取能量。但，可再生能源或环境中的射频能量会受到外部因素的影响，具有不确定性和不稳定性。因此，混合能量功能网络得到了广泛应用。在混合能量功能网络中，设备初始能量的大小会影响到网络的工作过程。当初始能量较小时，不需要开启无线能量传输过程，网络的工作时间将会全部用于上行信息传输以最大化系统的吞吐量，反之，当无线能量传输开启时，需要优化上下行的时间分配来提高系统的吞吐量。针对无线能量传输开启时间的问题，本文将混合无线供电通信网络的吞吐量最大化问题转化为凸优化问题，使用凸优化理论、拉格朗日乘数法和二分法求出了无线能量传输开启的条件；并在给定的系统传输时间内，通过上下行时间分配、能量发射基站的能量协方差矩阵以及用户信息传输的发射功率的优化最大化了上行非正交多址接入系统的吞吐量，求出了资源分配的最优闭式解，保证了所有用户设备之间资源分配的公平性。最后，该方案与各向同性波束成型策略、固定时间分配策略进行对比，证明了本文提出的算法具有更优越的吞吐量性能。

1 系统模型

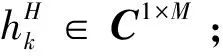
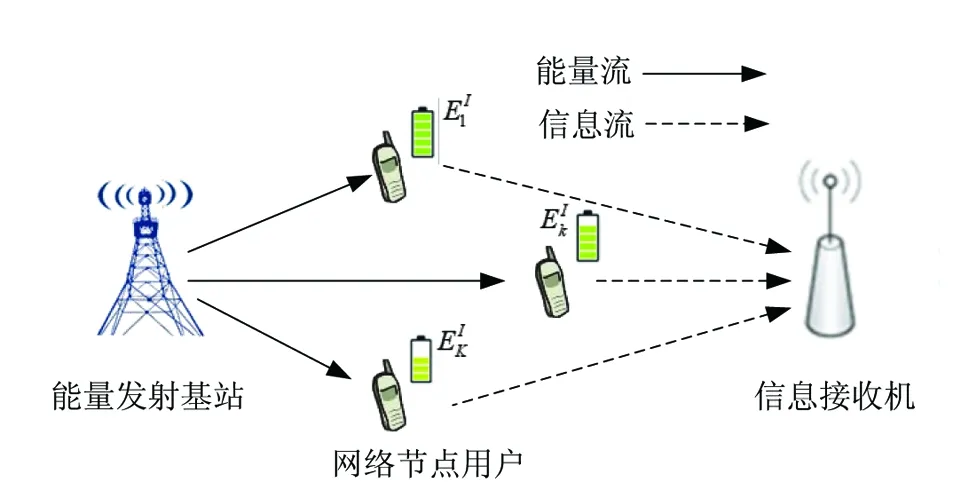
图1 系统模型Fig.1 System model

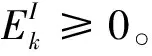
当下行能量传输阶段开启时，能量基站广播能量信号x∈CM×1给所有用户，持续时间为τ0，能量信号x协方差矩阵W受最大发射功率约束可表示为W=E(xxH)≤Pmax，其中Pmax为能量基站的最大发射功率。所以，用户k在能量传输阶段收集到的能量可表示为：

(1)

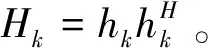
(2)

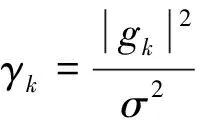
2 问题描述及算法分析

本文通过联合优化上下行时间分配、能量发射机的能量协方差矩阵W以及用户信息传输的发射功率Pk来最大化上行非正交多址接入系统的吞吐量，并分析无线能量传输开启的条件。因此优化问题描述如下：

(3a)

(3b)

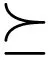
(3c)

τ0+τ≤Tmax

(3d)

τ≥0,τ0≥0,Pk≥0,∀k(3e) 问题(3)中约束(3b)表示用户信息传输使用的能量不会超过用户从自然环境和能量基站收集到的能量；约束(3c)为能量基站的最大发射功率约束，W为半正定矩阵；约束(3d)表示系统上下行总的传输时间不超过假设的最大时间Tmax；约束(3e)表示优化变量是非负的。

τ≥0,τ0≥0,ek≥0,∀k

(4)

显然问题(4)的目标函数为凹函数，约束为线性的。所以，问题(4)为标准的凸优化问题，可以很容易地使用内点法[18]求得问题的最优解。然而，内点法得到的数值结果无法揭示系统的内在工作机制。为了更好地观察系统的内在工作机制、无线能量传输阶段开启的条件以及无线能量传输开启时对应的最优解的结构，本文将采用凸优化理论分析这一过程。

2.1 无线能量传输开启条件以及资源分配策略

当下行无线能量传输开启时，为求得系统最大吞吐量最优解结构，有下面两个引理成立。

引理1 当无线能量传输阶段开启时，用户会消耗完所有可用的能量以达到最大的吞吐量。

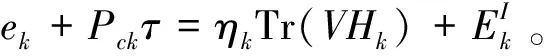
引理2 当无线能量传输阶段开启时，取得最大的吞吐量必须满足τ0+τ=Tmax。

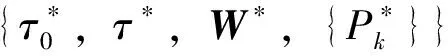
下面分析无线能量传输开启的条件以及吞吐量最大化资源分配算法。由于问题(4)为凸优化问题，且满足Slater’s条件[18]，这意味着问题(4)的最优解可以通过KKT条件求得，所以问题(4)的拉格朗日函数可表示为：

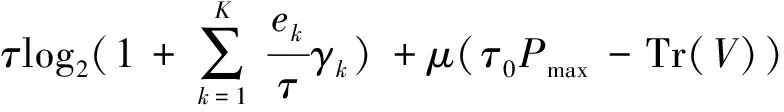
-ek-Pckτ)+δ(T-τ0-τ)

(5)

其中，μ、λk、δ为拉格朗日乘子。

让拉格朗日函数L分别对τ0,τ,ek求导，有

(6)

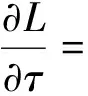
(7)

(8)

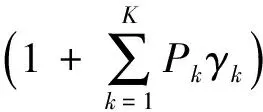
(9)

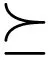
(10)

所以，进一步将(9)式等价变换为(11)式：

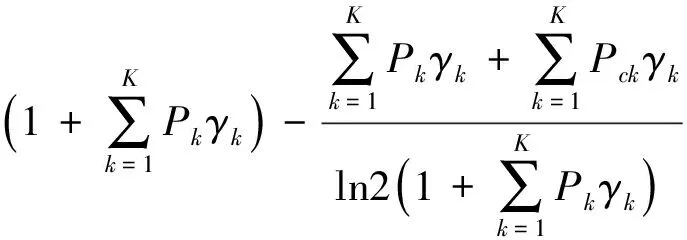
(11)

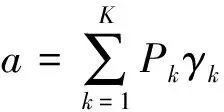
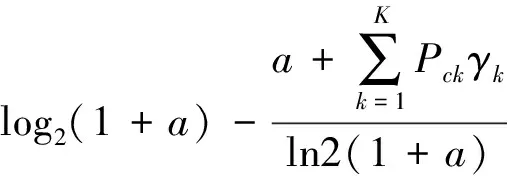
=0

(12)

对于方程(12)可以很容易使用二分法来求出唯一的最优解a*。

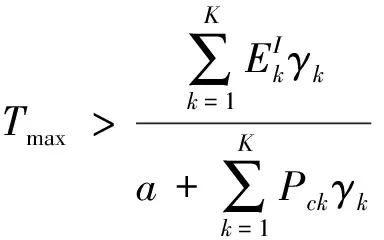
证明根据引理1，因为所有的用户会消耗完其收集到的能量，所以有

(13)

将(13)代入到引理2中有：

(14)

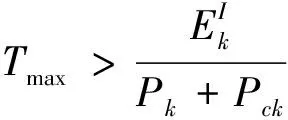
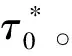
(15)

其中，a*为方程(12)的最优解。协方差矩阵最优解W*可通过与文献[19] 类似的方法求得，即：

(16)

其中，v为矩阵B取得最大特征值时对应的特征向量。

根据引理2可知当无线能量开启时，最优的无线信息传输时间τ*为：

(17)

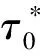
(18)

2.2 无线能量传输未开启时资源分配策略

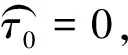
(19)

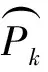
(20)

3 仿真结果与分析

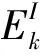
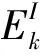
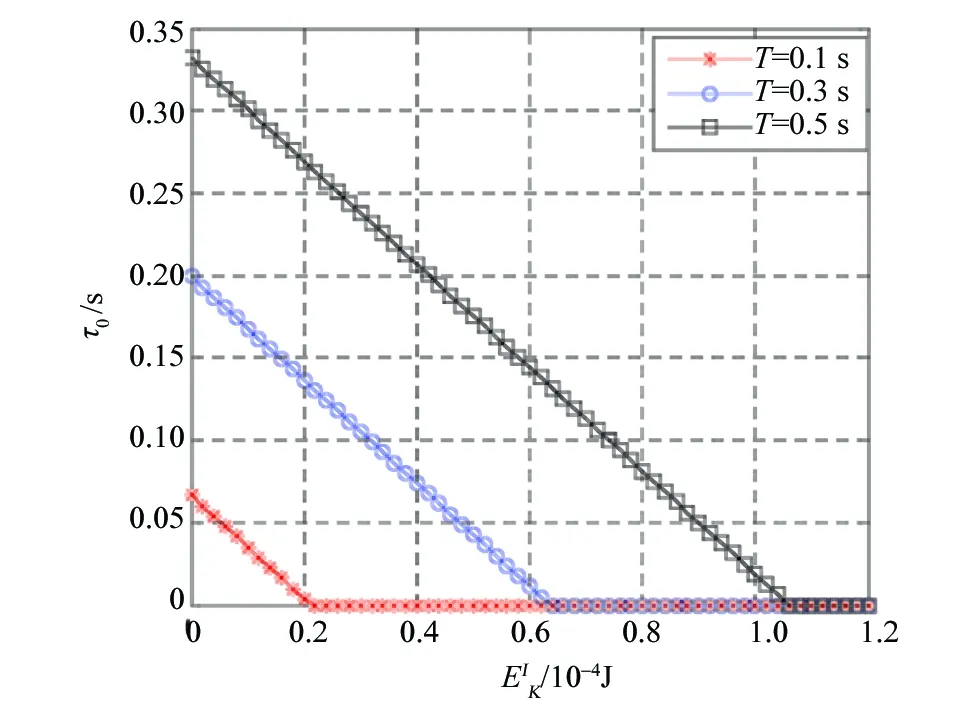
图2 无线能量传输时间随用户初始能量的变化Fig.2 Wireless energy transfer time vs user’s initial energy

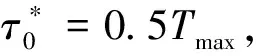
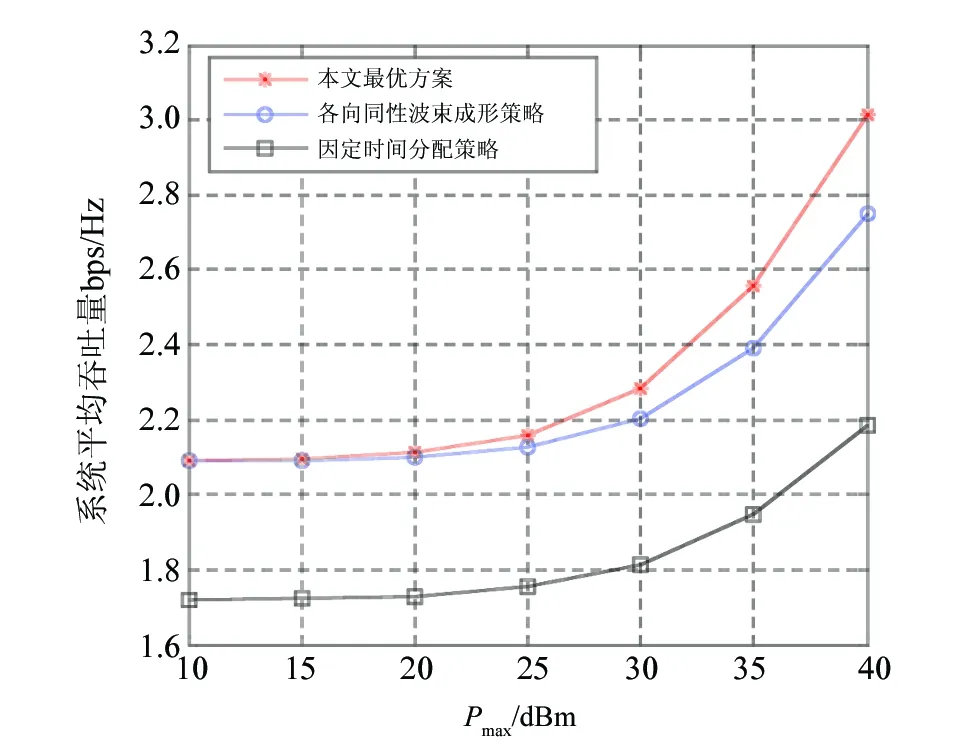
图3 系统平均吞吐量随基站最大发射功率的变化Fig.3 System average throughput vs the base station’s maximum transmit power

4 结束语

本文针对基于非正交多址接入的无线供电通信网络模型，研究了无线能量传输开启的条件；并通过优化上行时间分配、能量发射机的能量协方差矩阵以及用户信息传输的发射功率联合最大化上行非正交多址接入系统的吞吐量。仿真结果表明，与两种基准方案相比，本文提出的算法具有更好的吞吐量性能。