单圈图永久和的极值

陈兰，吴廷增

(青海民族大学数学与统计学院，青海 西宁 810007)

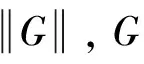
设G是一个有n个顶点的图。一个Sachs图是一个简单，它的每一个组成部分是独立的边或圈。设H是有k个顶点的图。用C(H)表示图H中圈的数。G的积和多项式定义为

其中A(G)为G的邻接矩阵，

图的积和多项式已被广泛研究，最近的研究见文献[1-5]。

图的永久和，记为PS(G),是指积和多项式π(G,x)的所有系数的绝对值的和，即

图的永久和是最近提出的概念。研究表明图的永久和在化学分子的物理、化学性质中表现非常活跃。文献[6]中发现了富勒烯C50(D5h)后，文献[7]中指出了C50(D5h)的永久和在C50中的271个非同构的富勒烯中达到最小，并指出永久和与分子图的稳定性密切相关。近年来,有一些关于永久和的重要结果被出版, 文献[8]确定了关于永久和的极值六边形链；文献[9]研究了八边形链永久和的性质；文献[10]刻画了树中最大和最小的永久和。

令Un为n阶连通单圈图集合。文献[10]和[11]分别刻画了n阶连通单圈图集合Un中最大、最小和次大、次小的永久和。在此结果的基础上，本文刻画了n阶连通单圈图集合Un中第三小直至第七小的永久和及其相应的图。

1 一些引理

证明主要结论之前,先列出或证明一些引理。

引理1[10]设T是一个n个顶点的树，则n≤PS(T)≤F(n+1)。

这里F(n+1)是第n+1个Fibonacci数，而且左边等号成立当且仅当T=Sn，右边等号成立当且仅当T=Pn。

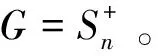
引理3[10]设图G和H是无公共顶点的图，则PS(G∪H)=PS(G)PS(H)。

引理4[10]

(i)e=uv是图G的一条边，C(e)是包含e的圈的集，则

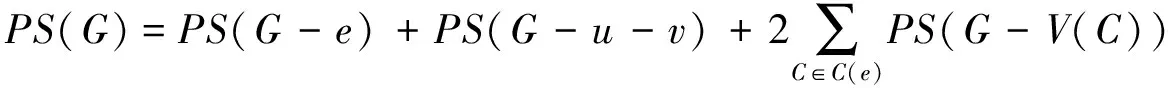
(ii)设v是图G的一个顶点，C(v)是包含v的圈的集，则

注1 如果一个图有个0顶点称为空图，记为∅，约定PS(∅)=1。

引理5[11]设

n≥5，则 3n-4≤PS(G)。

引理6[11]

(i) 当n≥3时，PS(Cn)=F(n+1)+F(n-1)+2；

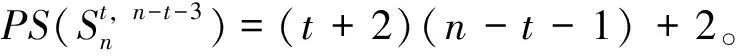
注2 由公式(ii)立即可得：

(iii)当n≥5且4≤r≤n-1时，PS(G″(r,n-r))=(n-r+1)F(r)+2F(r-1)+2。

注3 由公式(iii)立即可得：

PS(G″(4,n-4))=3n-3，PS(G″(5,n-5))=5n-12，PS(G″(6,n-6))=8n-28

(iv) 当n≥5且1≤s≤n-4时，PS(G′(n,n-3-s,s))=2(ns+n-s2-2s)。

注4 由公式(iv)立即可得：PS(G′(n,n-4,1))=2(2n-3),PS(G′(n,n-5,2))=2(3n-8)。

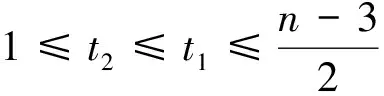
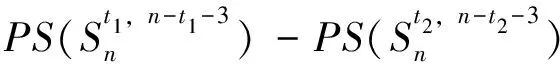
=[(t1+2)(n-t1-1)+2]-[(t2+2)(n-t2-1)+2]

=[(t1-t2)+2+t2][n-(t1-t2)-t2-1]+[(t1-t2)-2-t1][n+(t1-t2)-t1-1]

=(t1-t2)n-(t1-t2)2-(t1-t2)(t2+1)+(2+t2)n-(2+t2)(t1-t2)-(2+t2)(t2+1)

+(t1-t2)n+(t1-t2)2-(t1-t2)(t1+1)-(2+t1)n-(2+t1)(t1-t2)+(2+t1)(t1+1)

=(t1-t2)[(n-3)-(t1+t2)]≥0

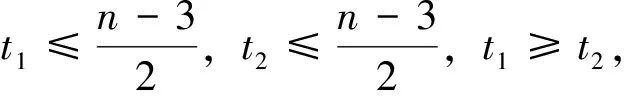
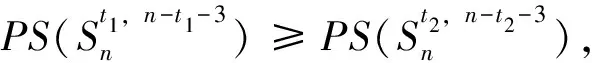
引理8 设4≤r≤n-1,

(i) 当r>4,n>5时，PS(G″(r,n-r))>PS(G″(4,n-4))。

(ii )当r>5,n>6时，PS(G″(r,n-r))>PS(G″(5,n-5))。

证明根据引理6(iii)，当r>4,n>5时 有

PS(G″(r,n-r))-PS(G″(r-1,n-r+1))

=[(n-r+1)F(r)+2F(r-1)+2]-[(n-r+2)F(r-1)+2F(r-2)+2]

=(n-r+1)F(r)-(n-r)F(r-1)-2F(r-2)=F(r)+(n-r-2)F(r-2)

=(n-r)F(r-2)+F(r-3)>0

所以当r>4,n>5时PS(G″(r,n-r))是r的严格增函数，因此结论成立。

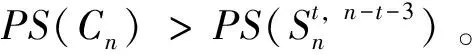
证明根据引理6(i)和(ii)，有

=F(n+1)+F(n-1)-(t+2)(n-t-1)

当6≤t≤n-9时，

F(n+1)+F(n-1)

=F(t)F(n-t+2)+F(t-1)F(n-t+1)+F(t)F(n-t)+F(t-1)F(n-t-1)

≥t(n-t+2)+(t-1)(n-t+1)+t(n-t)+(t-1)(n-t-1)

=(4t-2)(n-t-1)+6t-2

所以

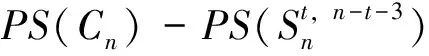
≥(4t-2)(n-t-1)+6t-2-(t+2)(n-t-1)

=(3t-4)(n-t-1)+6t-2>0

引理10 当4≤r≤n-1，n≥5时有PS(Cn)>PS(G″(r,n-r))。

证明根据引理6(i)和(iii)当4≤r≤n-1，n≥5时， 有

PS(Cn)-PS(G″(r,n-r))=[F(n+1)+F(n-1)+2]-[(n-r+1)F(r)+2F(r-1)+2]

=[F(n+1)-(n-r+1)F(r)]+[F(n-1)-2F(r-1)]

下面分三种情况证明：

(i) 当n-r≥3时

F(n+1)=F(n-r+2)F[(n+1)-(n-r+2)+1]+F(n-r+1)F[(n+1)-(n-r+2)]

=F(n-r+2)F(r)+F(n-r+1)F(r-1)

≥(n-r+2)F(r)+F(n-r+1)F(r-1)>(n-r+1)F(r)F(n-1)

=F(3)F[(n-1)-3+1]+F(2)F[(n-1)-3]

=2F(n-3)+F(n-4)≥2F(r)+F(n-4)>2F(r-1)

所以

PS(Cn)-PS(G″(r,n-r))>0，即PS(Cn)>PS(G″(r,n-r))

(ii) 当n-r=2时

PS(Cn)-PS(G″(r,n-r))=F(r+3)-3F(r)+F(r+1)-2F(r-1)

=F(r+3)-F(r)-2F(r+1)+F(r+1)

=F(r+3)-F(r)-F(r+1)=F(r+3)-F(r+2)>0

所以PS(Cn)>PS(G″(r,n-r))；

(iii)当n-r=1时

PS(Cn)-PS(G″(r,n-r))=F(r+2)-2F(r)+F(r)-2F(r-1)

=F(r+2)-2F(r+1)+F(r)

=F(r)-F(r-1)>0

所以PS(Cn)>PS(G″(r,n-r))。

因此 当4≤r≤n-1，n≥5时有PS(Cn)>PS(G″(r,n-r))。

引理11 当n≥7时有PS(Cn)>PS(G′(n,n-4,1))。

证明根据引理6(i)和(iv)当n≥7时有

PS(Cn)-PS(G′(n,n-r-4,1))=[F(n+1)+F(n-1)+2]-(4n-6)

=F(n)+2F(n-1)-4n+8=3F(n-1)+F(n-2)-4n+8

≥3(n-1)+(n-2)-4n+8=3>0

这里因为n≥7，所以

n-1≥n-2≥5,F(n-1)≥n-1,F(n-2)≥n-2

因此当n≥7时, 有PS(Cn)>PS(G′(n,n-4,1))。

变换1[11]设u是图G0的一个顶点，图G1表示把G0的顶点u和树T一个顶点v用一条边相连接的图，图G2表示把G0的顶点u和星S|T|的中心用一条边相连接的图，把从图G1变换到到图G2称为变换1。

引理12[11]设图G1和图G2如变换1所定义，则PS(G1)≥PS(G2) 等号成立当且仅当T

是一个星并且v是T的中心。

变换2[11]设图G2如变换1所定义，用G3表示增加G2中星S|T|的一个悬挂边并且把星S|T|的中心和G0的顶点u粘在一起的图，把从图G2变换到到图G3称为变换2。

引理13[11]设图G2和图G3如变换1和变换2所定义，则PS(G2)≥PS(G3)，等号成立当且仅当T=K1或u是G0的孤立点。

变换3[11]设G0是一个单圈图并且Cr=u1u2uru1是G0唯一的圈，设ui和uj是G0的两个度为2 的顶点，1≤i≤j≤r，用G1表示分别把s≥1个和t≥1个悬挂点连接到图G0的两个顶点ui和uj的图；用G2表示把s+t个悬挂点连接到G0的顶点uj的图；用G3表示把s+t个悬挂点连接到G0的顶点ui的图。把从图G1变换到到图G2或从图G1变换到到图G3称为变换3。

引理14[11]设图G1，G2和G3如变换3所定义，则PS(G1)>PS(G2)或PS(G1)>PS(G3)。

2 主要结论

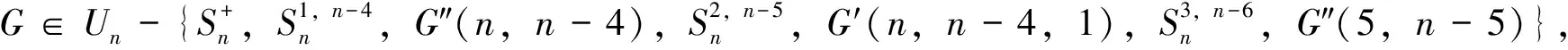
(i)PS(G)>PS(G″(4,n-4))=3n-3;

(iii)PS(G)>PS(G′(n,n-4,1))=4n-6;

(v)PS(G)>PS(G″(5,n-5))=5n-12。

证明设单圈图G中唯一圈的圈长为r。下面分三种情况证明：

情形1 当r=n时，则G=Cn。

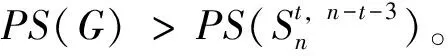
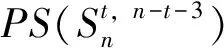
根据引理10, 当n≥5时，PS(G)>PS(G″(4,n-4))，PS(G)>PS(G″(5,n-5))；

根据引理11, 当n≥7时有PS(G)>PS(G′(n,n-4,1))。

因此 当r=n，n≥17时，有下面不等式成立

(i)PS(G)>PS(G″(4,n-4))=3n-3;

(iii)PS(G)>PS(G′(n,n-4,1))=4n-6;

(v)PS(G)>PS(G″(5,n-5))=5n-12。

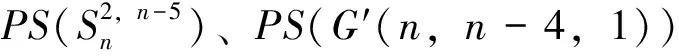
因此 当4≤r≤n-1，n≥17时，有下面不等式成立

(i)PS(G)>PS(G″(4,n-4))=3n-3;

(iii)PS(G)>PS(G′(n,n-4,1))=4n-6;

(v)PS(G)>PS(G″(5,n-5))=5n-12。

情形3 当r=3时，设C是G中唯一圈长为3的圈。由于n≥17，故C中至少一个顶点的度超过2。

子情形3.1C中至少有两个顶点的度超过2。因为

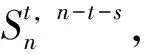
因此 当r=3，n≥17且G中唯一圈C中至少两个顶点的度超过2时，有下面不等式成立

(i)PS(G)>PS(G″(4,n-4))=3n-3;

(iii)PS(G)>PS(G′(n,n-4,1))=4n-6;

(v)PS(G)>PS(G″(5,n-5))=5n-12。

根据引理6(iv)和注4有PS(G′(n,n-3-s,s))-PS(G′(n,n-5,2))=2(ns+n-s2-2s)-2(3n-8)=2(s-2)(n-s-4)≥0,上式当s≥2，且n-s-3≥1时成立，等号成立当且仅当s=2或n-s-3=1。所以当s≥2且n>7时有PS(G′(n,n-3-s,s))≥PS(G′(n,n-5,2))。

又根据引理6(ii)注2，(iii)注3和(iv)注4，显然当n≥17时有

PS(G′(n,n-5,2))>PS(G″(5,n-5))

因此 当r=3，n≥17且G中唯一圈C中只有一个顶点的度超过2时，有下面不等式成立

(i)PS(G)>PS(G″(4,n-4))=3n-3;

(iii)PS(G)>PS(G′(n,n-4,1))=4n-6;

(v)PS(G)>PS(G″(5,n-5))=5n-12。

综合上面三种情形：当G是一个单圈图，并且n≥17，

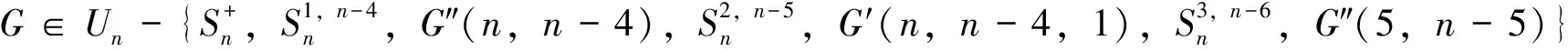
(i)PS(G)>PS(G″(4,n-4))=3n-3;

(iii)PS(G)>PS(G′(n,n-4,1))=4n-6;

(v)PS(G)>PS(G″(5,n-5))=5n-12。

定理1证毕。

定理2 设G是一个n(n≥17)个顶点的单圈图。

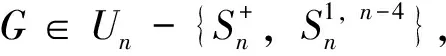
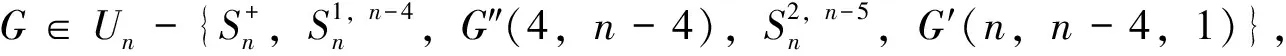
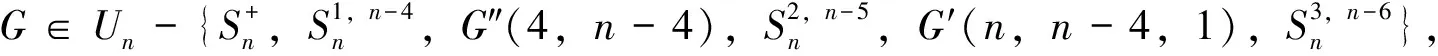
证明根据引理6(ii)注2、(iii)注3和(iv)注4，显然当n≥17时，有3n-3<4n-10<4n-6<5n-18<5n-12成立，所以当n≥17时，有下面不等式成立

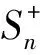
备注根据引理6、引理12、引理13和引理14容易得单圈图顶点数分别是n=8,9,10,,16时单圈图永久和第三小到第七小的图如下所示：

(i) 当n=8时，第三小到第七小永久和的图分别是：

G′(8,4,1)，G″(5，3)和G′(8,3,2)。

(ii) 当n=9时，第三小到第七小永久和的图分别是;

G′(9，5,1)和G″(5,4)。

(iii) 当n=10时，第三小到第七小永久和的图分别是:

G′(10，6,1)和G″(5,5)。

(iv) 当n=11时，第三小到第七小永久和的图分别是:

和G″(5,6)。

(v) 当n=12时，第三小到第七小永久和的图分别是:

和G″(5,7)。

(vi) 当n=13时，第三小到第七小永久和的图分别是：

(vii) 当n=14时，第三小到第七小永久和的图分别是：

(viii) 当n=15时，第三小到第七小永久和的图分别是：

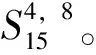
(ix) 当n=16时，第三小到第七小永久和的图分别是：