平实中见本质 融合中显精彩

【摘 要】 向量兼显“数”的严谨与“形”的直观，是沟通代数与几何的重要工具.纵观2019年全国数学高考中的向量试题，平实中彰显数学本质，融合中呈现精彩方法.从考查的重点知识、解决的主要途径、试题的总体分布以及与其它知识的交汇等方面对2019年高考向量问题进行评析，归结出一些对高考向量复习的合理化建议.

【关键词】 2019年高考;向量;试题;评析

1 高考对“向量”的考查要求

在普通高中数学课程标准（2017版）中，对“向量”知识进行了深度刻画，其内容包括：“掌握向量的线性运算，了解向量的基本定理并掌握其坐标表示，会进行向量数量积的运算，能用向量语言和方法表述和解决数学和物理中的一些问题，发展运算能力和解决实际问题的能力”＼[1＼].所以学生首先应正确理解向量的概念和几何意义，并能进行向量的运算操作;其次在形与数的转化中灵活地解决问题，体现向量解题的工具性作用.2019年全国高考向量试题遵循了“考查基础知识的同时，注重方法和素养考查”的原则.在知识层面，直接考查向量的线性运算、数量积、垂直或平行、基底、模或夹角等;在方法层面，重点考查数形结合、化归、分类讨论等思想方法;在素养层面，主要考查数学运算、直观想象和逻辑推理等核心素养.

2 2019年高考向量试题的总体分布和解决途径

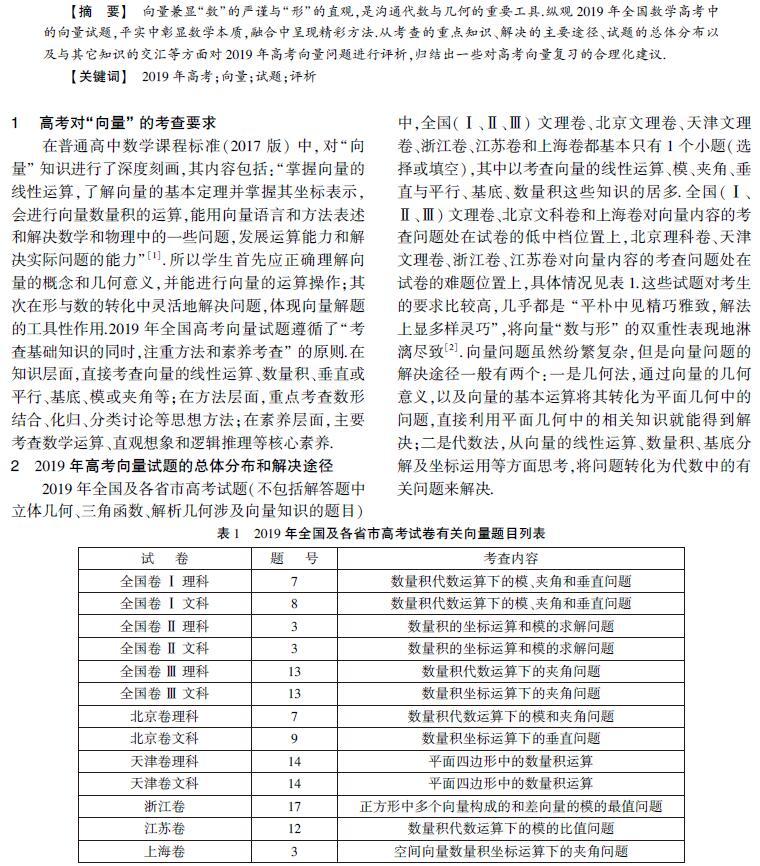
2019年全国及各省市高考试题（不包括解答题中立体几何、三角函数、解析几何涉及向量知识的题目）中，全国（Ⅰ、Ⅱ、Ⅲ）文理卷、北京文理卷、天津文理卷、浙江卷、江苏卷和上海卷都基本只有1个小题（选择或填空），其中以考查向量的线性运算、模、夹角、垂直与平行、基底、数量积这些知识的居多.全国（Ⅰ、Ⅱ、Ⅲ）文理卷、北京文科卷和上海卷对向量内容的考查问题处在试卷的低中档位置上，北京理科卷、天津文理卷、浙江卷、江苏卷对向量内容的考查问题处在试卷的难题位置上，具体情况见表1.这些试题对考生的要求比较高，几乎都是 “平朴中见精巧雅致，解法上显多样灵巧”，将向量“数与形”的双重性表现地淋漓尽致＼[2＼].向量问题虽然纷繁复杂，但是向量问题的解决途径一般有两个：一是几何法，通过向量的几何意义，以及向量的基本运算将其转化为平面几何中的问题，直接利用平面几何中的相关知识就能得到解决;二是代数法，从向量的线性运算、数量积、基底分解及坐标运用等方面思考，将问题转化为代数中的有关问题来解决.

3 2019年高考向量试题的评析

向量在知识的呈现上，既具有加减、数乘和数量积运算的代数形式，又兼备加减、数乘和数量积运算的几何意义，呈现形式的多样性和解决方法的灵活性给高考提供了多渠道的命题视角.笔者以2019年高考数学全国文理和各省市文理13份真题卷为例，撷取若干典型问题进行评析.

3.1 加强向量基本运算的考查

平面向量的线性与数量积运算环境下平行、垂直、夹角和模的问题是平面向量的基础内容，它们成为了高考考查的基点.

3.1.1 坐标运算

例1 （2019年上海3）若a=（1，0，2），b=（2，1，0），则a与b的夹角为

.

例2 （2019年北京文9）已知向量a=（-4，3），b=（6，m），且a⊥b，則m=

.

例3 （2019年全国Ⅲ文13）已知向量a=（2，2），b=（-8，6），则cos〈a，b〉=

.

例4 （2019年全国Ⅱ理3）已知AB=（2，3），AC=（3，t），|BC|=1，则AB·BC=

.

A.-3B.-2C.2D. 3

例5 （2019年全国Ⅱ文3）已知向量a=（2，3），b=（3，2），则|a-b|=（）.

A.2B.2C.52D. 50

3.1.2 代数运算

例6 （2019年全国Ⅰ理7文8）已知非零向量a，b满足|a|=2|b|，且（a-b）⊥b，则a与b的夹角为（）.

A.π6B.π3C.2π3D. 5π6

例7 （2019年全国Ⅲ理13）已知a，b为单位向量，且a·b=0，若c=2a-5b，则cos〈a，c〉=

.

评析 2019年高考，低中等难度的向量问题的考查基本上是基于线性和数量积运算，从坐标和代数运算两种方式，展开对平行、垂直、夹角和模等问题的考查.学生只要熟练掌握好向量的线性和数量积运算的有关知识，特别是熟练掌握平行、垂直、夹角、模与数量积的关系就可以迎刃而解. 向量基本运算既是高考对向量考查的基点，又是推理论证、运算求解、联系迁移的依据.

3.2 重视几何推理与向量运算相结合

由于向量兼具几何和代数的特性，2019年高考向量试题的解决，既要注重向量运算（代数与坐标运算），同时也需要几何推理相辅助，以达到几何推理与向量运算的融合使用.

例8 （2019年江苏12）如图1，在△ABC中，D是BC的中点，E在边AB上，BE=2EA，AD与CE交于点O.若AB·AC=6AO·EC，则ABAC的值是

.

解 法1 作AF∥BC交CE的延长线于点F，故AFBC=AEEB=12，所以AF=12BC=CD，所以AO=OD，故AB·AC=6AO·EC=3AD·EC=3×12（AB+AC）×（AC-13AB）.

化简得3|AC|2=|AB|2，所以ABAC=3.

法2 过D作DG∥AB，由于DG瘙 綊 12BE，BE=2EA，所以AE瘙 綊 DG，所以AO=OD，下同解法1.

法3 作DH∥CE，则BH=HE=EA，所以AO=OD，下同解法1.

法4 作EI∥BC，则IEBD=IECD=13，所以IOOD=13，而AIID=12，所以AO=OD，下同解法1.

法5 由梅氏定理可知AEEB·BCCD·DOOA=1，而D是BC的中点，BE=2EA，所以AO=OD，下同解法1.

法6 AD=12（AB+AC），令AO=λAD，则AO=λ2（AB+AC）=3λ2AE+λ2AC，由于E，O，C三点共线，所以3λ2+λ2=1，故λ=12，所以所以AO=OD，下同解法1.

法7 设AO=λAD=λ2（AB+AC），另一方面AO=μ（13AB）+（1-μ）AC，所以12λ=13μ，

12λ=1-μ，

解得λ=12，下同解法1.

例9 （2019年天津理14文14）在四边形ABCD中，AD∥BC，AB=23，AD=5，∠A=300，点E在线段CB的延长线上，且AE=BE，则BD·AE=

.

法1 BD·AE=（BA+AD）·（AB+BE）=-|AB|2+BA·BE+AD·AB+AD·BE=-12+6+15-10=-1.

法2 BD·AE=（BA+AD）·AE=BA·AE+AD·AE=23×2×cos1500+5×2×cos600=-1.

法3 BD·AE=（BE+EA+AD）·AE=-2-4+5=-1.

法4 如图2，建立平面直角坐标系，则A（0，0），B（3，3），E（1，3），D（5，0），所以AE=（1，3），BD=（2，-3），BD·AE=2-3=-1.

法5 作BF∥AE，设∠CBD=θ，BD=25+12-2×5×23×32=7，sinθ=37，cosθ=27.cos∠FBD=cos（θ+π3）=-714，BD·AE=7×2×（-714）=-1.

法6 过B作BH⊥AD，则BD·AE=（25AD-HB）·（15AD+HB）=225×25-3=-1.

法7 取AB的中点M，由于AE=BE，所以EM⊥AB，BD·AE=（AD-AB）·（AM+ME）=AD·AM+AD·ME-AB·AM-AB·ME =152-52-6=-1.

法8 BD·AE=（BH+HD）·（AH+HB+BE）=6-3-4=-1.

评析 以上两个高考向量问题都具有一定的综合性、灵活性和解法的发散性.代数运算和坐标运算相结合，几何推理和向量运算相结合，直接运算和转化运算相结合，坐标基底和非坐标基底相结合，向量“身份”的多元性生发了解决方法的“融合”性.

2.3 突出向量与其它知识的交汇

数学的抽象性、系统性和严密性决定了数学知识之间存在深刻的内在联系.平面向量作为中学数学知识的一个交汇点，成为联系多项内容的桥梁，特别是与不等式、函数、几何等知识都有着深刻的内在联系.因此，向量与其它知识的交汇自然受到高考命题者青睐.

例10 （2019年北京理7）设点A，B，C不共线，则“AB与AC的夹角为锐角”是“|AB+AC|>|BC|”的（）.

A.充分而不必要條件B.必要而不充分条件

C.充分必要条件D.既不充分也不必要条件

法1 AB与AC的夹角为锐角AB·AC>0|AB+AC|2-|BC|2=（|AB|2+|AC|2+2|AB||AC|cosθ）-（|AB|2+|AC|2-2|AB||AC|cosθ）=4AB·AC>0|AB+AC|>|BC|.

法2 AB与AC的夹角为锐角AB·AC>0且|AB|2+|AC|2-|BC|2>0|AB+AC|2-|BC|2=（|AB|2+|AC|2-|BC|2）+2AB·AC>0|AB+AC|>|BC|.

法3 |AB+AC|>|BC||AB+AC|>|AC-AB|AB·AC>0AB与AC的夹角为锐角.

例11 （2019年浙江17）已知正方形ABCD的边长为1，当每个λi（i=1，2，3，4，5，6）取遍±1时，|λ1AB+λ2BC+λ3CD+λ4DA+λ5AC+λ6BD|的最小值为

，最大值为

.

解法1 |λ1AB+λ2BC+λ3CD+λ4DA+λ5AC+λ6BD|=|λ1AB+λ2AD-λ3AB-λ4AD+λ5（AB+AD）+λ6（AD-AB）|=|（λ1-λ3+λ5-λ6）AB+（λ2-λ4+λ5+λ6）AD|=[（λ1-λ3）+（λ5-λ6）]2+[（λ2-λ4）+（λ5+λ6）]2（*）

由于每个λi（i=1，2，3，4，5，6）可独立取遍±1，（*）式中λ1-λ3和λ2-λ4都可独立取-2，0，2，而λ5-λ6和λ5+λ6取值范围也为-2，0，2，不管λ5-λ6和λ5+λ6如何取值，只要λ1-λ3=λ6-λ5且λ2-λ4=-（λ5+λ6）时，|λ1AB+λ2BC+λ3CD+λ4DA+λ5AC+λ6BD|取到最小值为0.

另一方面

[（λ1-λ3）+（λ5-λ6）]2+[（λ2-λ4）+（λ5+λ6）]2≤（2+|λ5-λ6|）2+（2+|λ5+λ6|）2=8+2（λ52+λ62）+4（|λ5-λ6|+|λ5+λ6|）=8+2（1+1）+4×2=25.

所以|λ1AB+λ2BC+λ3CD+λ4DA+λ5AC+λ6BD|的最大值为25.

法2 如图4，建立平面直角坐标系，则A（0，0），B（1，0），C（1，1），D（0，1）则|λ1AB+λ2BC+λ3CD+λ4DA+λ5AC+λ6BD|=

|λ1（1，0）+λ2（0，1）+λ3（-1，0）+λ4（0，-1）+λ5（1，1）+λ6（-1，1）|=

|（λ1-λ3+λ5-λ6，λ2-λ4+λ5+λ6）|

=[（λ1-λ3）+（λ5-λ6）]2+[（λ2-λ4）+（λ5+λ6）]2.

下同解法1.

法3 令AB=e1，BC=e2，则AC=e1+e2，BD=e2-e1，记λ5AC+λ6BD=e3，那么|λ1AB+λ2BC+λ3CD+λ4DA+λ5AC+λ6BD|=|λ1e1+λ2e2-λ3e1-λ4e2+e3|=|（λ1-λ3）e1+（λ2-λ4）e2+e3|.

由于λ1-λ3和λ2-λ4都可独立取-2，0，2，e3=λ5AC+λ6BD=（λ5-λ6）e1+（λ5+λ6）e2=±2e1或±2e2.当λ1-λ3=2，λ2-λ4=0，e3=-2e1时，|（λ1-λ3）e1+（λ2-λ4）e2+e3|取到最小值为0;另一方面|（λ1-λ3）e1+（λ2-λ4）e2+e3|≤|2e1+2e2+2e1|=|4e1+2e2|=25，当λ1-λ3=2，λ2-λ4=2，e3=2e1时可以取到最大值为25.

评析 向量的知识交汇型试题是考查学生的知识统整能力、数学思想方法的综合运用能力和逻辑思维能力的題型，以上两个高考向量问题注重了向量与不等式、离散取值的多变量函数等知识的融合，凸显了向量问题中基底思想的应用，应予以关注. 在复习向量时，可重点关注向量与几何、函数、三角、不等式等知识的交汇.在解决的途径上一般也可以从几何和代数两个方面来入手，将其转化为平面几何问题或从向量的线性运算、数量积、基底分解及坐标运用等方面思考，将问题转化为代数中的有关问题来解决.

参考文献

[1] 中华人民共和国教育部.普通高中数学课程标准（2017年版）＼[S＼].北京：人民教育出版社，2018.1.

[2] 方孝钏.精美的高考向量试题中挥不去的几何情结＼[J＼].中国数学教育，2011（10）：24-26.

作者简介 方治（1978—），男，浙江省义乌中学科研处主任，中学高级教师，主要研究方向为数学与数学教育. 曾荣获全国优秀教练员、浙江省教坛新秀、浙江省师德楷模、浙派名师培养人选，个人执笔的课题获省一等奖一次，省二等奖一次，有多篇论文发表.