主题思想下的合情推理教学设计探讨
胡晋宾 刘洪璐

【摘 要】 合情推理在《普通高中数学课程标准(2017年版)》中的地位并没有被淡化,而是以逻辑推理中的核心素养形式得到强化. 合情推理的教学可以超越归纳和类比的方法讲解以及解题训练,基于主题思想理念中的核心素养和文化观念立意,采用数学文化欣赏的方式开展.
【关键词】 主题思想;合情推理;文化观念
1 开课缘起
《普通高中数学课程标准(2017年版)解读》中提出,“数学主题通常由数学教师根据教学需要来决定,它以重要的数学概念或核心数学知识为主线组织,或以数学思想方法为主线组织,或以数学学科核心素养、基本能力为主线组织”[1]. 2018年11月30日是南师附中一年一度的教学公开日,刘洪璐选择了“合情推理”,以核心素养和文化观念为主题立意,开设了公开课并进行了网络同步直播. 开课之后,苏教版高中数学教材主编、江苏省中小学教研室李善良教授进行了点评,多位专家和同行给予了肯定和鼓励. 以下基于当时的教学录像,对该设计进行梳理和反思.
2 简要流程
2.1 创设教学情境
【情境1】 师:前不久老师嗓子发炎,医生开了一款消炎药,这是药品说明书. (呈现某药品说明书)大多药品说明书上,都有采用动物做实验的疗效说明. 请问:人类药品实验为什么多用老鼠和狗等动物来做?
生1:因为老鼠和人在结构上有相似之处,都是哺乳动物,所以我们可以推断,在动物身上的实验结果可以类推到人类身上.
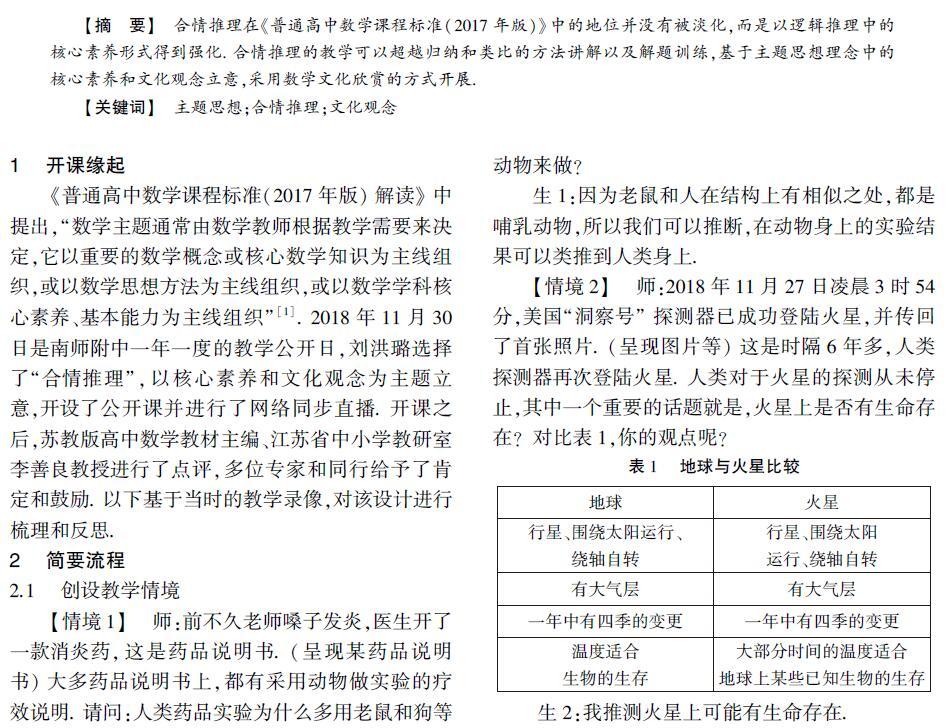
【情境2】 师:2018年11月27日凌晨3时54分,美国“洞察号”探测器已成功登陆火星,并传回了首张照片. (呈现图片等)这是时隔6年多,人类探测器再次登陆火星. 人类对于火星的探测从未停止,其中一个重要的话题就是,火星上是否有生命存在?对比表1,你的观点呢?
生2:我推测火星上可能有生命存在.
师:这位小科学家,(出示)【问题1】请问你做出这样的猜想的推理过程是怎样的?
生2:因为火星在结构上具有很多和地球相似的特征,所以我由地球存在生命,推测出火星上有可能有生命存在.
师:【情境3】大家知道鲁班发明锯子的故事吗?你能给大家讲讲这个故事并说明鲁班发明锯子的思路吗?(呈现鲁班及发明锯子的图片等)
生3:(简述鲁班发明锯子的故事略)我觉得鲁班发现小草是齿形的,可以划伤人,从而从结构上的相似性,即如果有一样东西也是齿形的边缘,那么它们在功能上也应该是相似的,即可以割断东西.
2.2 引出类比推理
师:像这样的由两类对象之间在某些方面的相似或相同,推演出它们在其他方面也相似或相同,这样的推理通常称为类比推理. 其实,这样的推理在数学中也很常见,比如:类比平面向量,学习空间向量;类比等差数列,学习等比数列;类比平面几何,学习立体几何;等等. 所以,著名数学家G·波利亚曾说:“类比是一个伟大的引路人,求解立体几何问题往往依赖于平面几何中的类比问题. ”(配图和名言)既然如此,我们来看下题.
【问题2】 如下图,在Rt△ABC中,∠C=90°,由勾股定理得c2=a2+b2. 类比平面内直角三角形的勾股定理,试给出空间中相关的猜想.
勾股定理的空间猜想生4:(上黑板简述猜想过程和证明思路)从平面中的三角形,我想类推到空间中四面体的相关性质,而且是直角三角形,所以就类推到3个侧面两两垂直的四面体P-DEF中的相关性质. 在平面上是边和边之间的关系,类比到空间中就想到面积之间的关系,从而有以下的猜想:设∠PDF=∠PDE=∠EDF=90°. S1,S2,S3和S分别表示△PDF,△PDE,△EDF和△PEF的面积,S2=S21+S22+S23. (该生给出了大致证明,过程省略)
师:这个猜想是否成立,需要严谨论证. 因为时间关系,课后自行完善. 教师出示【问题3】你能再举几个数学中,类比推理的例子吗?
生:学生们讨论踊跃,有的根据平面三角形面积和内切圆半径的关系S=12(a+b+c)r,其中,a,b,c为三角形的边长,r为三角形内切圆的半径,类比到空间中得到四面体的体积为13(S1+S2+S3+S4)r,(S1,S2,S3,S4为4个面面积,r为内切球半径)有的类比平面上圓的性质得到空间中球的性质,等等.
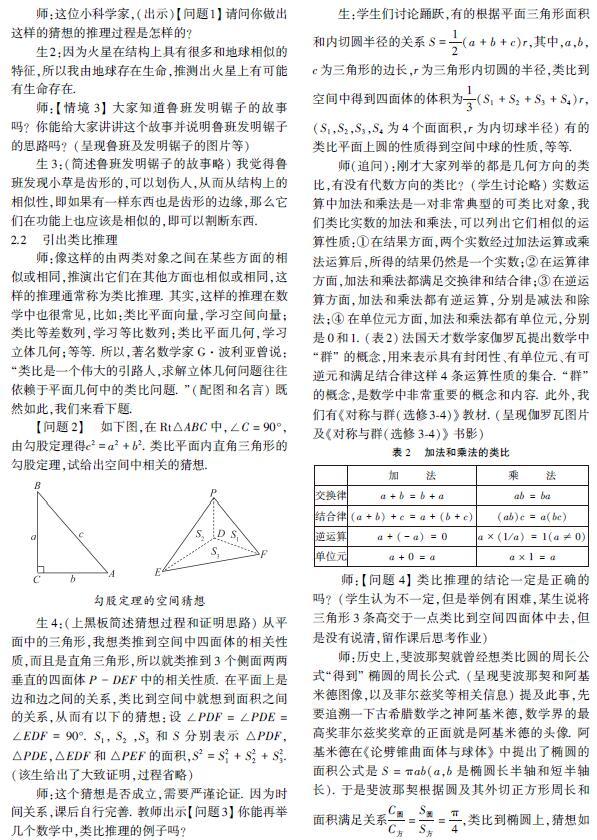
师(追问):刚才大家列举的都是几何方向的类比,有没有代数方向的类比?(学生讨论略)实数运算中加法和乘法是一对非常典型的可类比对象,我们类比实数的加法和乘法,可以列出它们相似的运算性质:①在结果方面,两个实数经过加法运算或乘法运算后,所得的结果仍然是一个实数;②在运算律方面,加法和乘法都满足交换律和结合律;③在逆运算方面,加法和乘法都有逆运算,分别是减法和除法;④在单位元方面,加法和乘法都有单位元,分别是0和1. (表2)法国天才数学家伽罗瓦提出数学中“群”的概念,用来表示具有封闭性、有单位元、有可逆元和满足结合律这样4条运算性质的集合. “群”的概念,是数学中非常重要的概念和内容. 此外,我们有《对称与群(选修34)》教材. (呈现伽罗瓦图片及《对称与群(选修34)》书影)
师:【问题4】类比推理的结论一定是正确的吗?(学生认为不一定,但是举例有困难,某生说将三角形3条高交于一点类比到空间四面体中去,但是没有说清,留作课后思考作业)
师:历史上,斐波那契就曾经想类比圆的周长公式“得到”椭圆的周长公式. (呈现斐波那契和阿基米德图像,以及菲尔兹奖等相关信息)提及此事,先要追溯一下古希腊数学之神阿基米德,数学界的最高奖菲尔兹奖奖章的正面就是阿基米德的头像. 阿基米德在《论劈锥曲面体与球体》中提出了椭圆的面积公式是S=πab(a,b是椭圆长半轴和短半轴长). 于是斐波那契根据圆及其外切正方形周长和面积满足关系C圆C方=S圆S方=π4,类比到椭圆上,猜想如果椭圆及其外切矩形的周长之比也能满足关系C椭C矩=S椭S矩=π4,就可以得到C椭=π(a+b). 遗憾的是,这个类比的结论是错误的. 根据微积分知识,可以写出椭圆周长的定积分公式,但由于被积函数的原函数不是初等函数,所以椭圆周长没有简洁的初等公式(虽然有近似公式,但是不精确).
第三,毋庸讳言,日常教学中我们确实关注更多的是演绎推理. 考虑到此次授课学生的基础比较好(年级中程度最好班级),对于他们来说,关键不是吃不吃得饱的问题而是吃不吃得好的问题,学会怎样提出与发现问题比分析与解决问题更为关键. 对于他们来说,开阔数学视野、培养数学兴趣比具体学习知识、解决问题,即便不是更为重要也是同等重要. 具体结合本次公开课,我们以合情推理为载体和纽带,借助问题串这一思维线索形式,串联起既往数学知识和数学故事,进行了数学文化的欣赏尝试.
3.2 关于教学主线的立意定位
本节课中,我们选择核心素养和文化观念作为两个主题思想进行设计突破.
第一,在核心素养路径方面,具体体现在:用类比的观点来审视,既往空间向量、等比数列和立体几何的学习,分别是通过平面向量、等差数列和平面几何类比得到;实数的加法和乘法可以作类比,并提炼出“群”的概念;斐波那契数列递推公式,可以通过归纳轻松得到;哥德巴赫猜想乃至费马大定理等著名数学问题,也可从归纳中得到验证. 等等. “三会”的巧妙运用:用数学的眼光来看待新药试制、锯子发明、火星猜想,用推理的思维来解读一叶知秋等谚语,用生活中的素材比如吃药等作为课程资源,用学科交叉的情境来阐述合情推理. 等等. 上述设计体现的设想是:数学知识的内部是有前后联系的,数学知识和生活以及其他学科是互动的,数学思维就在身边并且无处不在,数学学习不仅要关注知识技能而且要关注能力素养.
第二,在文化观念路径方面,数学学习不仅仅是知识的学习、能力的提高,而且有思维的养成和文化的熏陶. “数学文化是指数学的思想、精神、语言、方法、观点,以及它们的形成和发展;还包括数学在人类生活、科学技术、社会发展中的贡献和意义,以及与数学相关的人文活动”[2].本节课中,我们采用了许多数学史的经典内容,巧妙穿插在教学过程中,有意识地渗透数学文化欣赏.设计传递的观念是:人事有代谢,往来成古今;数学是由人来发展和完善的,不是与人无关的、不食人间烟火的;数学的发展不是一帆风顺的,而是可误曲折的;演绎推理只是数学的一个侧面,合情推理在创造发明中功不可没;数学是生动有趣的、富有人情的,而不是高高在上的、枯燥乏味的.
参考文献
[1] 史宁中,王尚志. 普通高中数学课程标准(2017年版)解读\[M\],北京:高等教育出版社,2018:253.
[2] 中华人民共和国教育部. 普通高中数学课程标准(2017年版)\[M\]. 北京:人民教育出版社,2018:10.
作者简介 胡晋賓(1975—),男,正编审职称(正高),博士,主要从事数学课程与教学论的教学及研究等工作.
刘洪璐(1979—),女,中教高级职称,硕士,主要从事高中数学教学设计与研究等. 南京市优秀青年教师,2010年第五届全国青年数学教师优秀课展示活动一等奖获得者.

