基于激光扫描臂的中子谱仪样品台回转轴误差辨识
韩志强,李群明~3,张绪烨
(1.中南大学 机电工程学院,长沙 410083;2.中南大学轻合金研究院,长沙 410083;3.中南大学高性能复杂制造国家重点实验室,长沙 410083)
0 引言
中子谱仪样品台是中子应力谱仪的重要部件之一[1],主要由X、Y向平移运动机构,Z向垂直升降机构和绕Z轴旋转运动机构组成,可实现四个自由度的运动(如图1所示),其运动精度要求在30um以内,回转轴几何误差是四轴中子谱仪样品台误差来源的主要因素之一,相对于直线轴误差,回转轴几何误差对平台的精度影响更大[2],因此对中子谱仪样品台回转误差辨识意义重大。三轴运动平台21项几何误差的辨识方法已比较完善,包括采用激光干涉仪的九线法[3],12线法[4],然而对于回转轴几何误差辨识的研究大多是集中在五轴数控机床的回转轴上,国内外普遍采用3D探头[5]、球杆仪[6],其中基于球杆仪的回转轴误差辨识方法较多,Tsutsumi等[7]采用三轴同步运动将球杆仪分别置于旋转轴的轴向、径向和切向三个位置进行回转轴几何误差辨识,Lee等[8]用球杆仪辨识回转轴的垂直误差和位置误差,对误差精度进行不确定性分析,这些方法为中子谱仪样品台回转轴的几何误差辨识提供了一定参考,但是目前回转轴的回转误差辨识方法均需要将测量仪器安装在被测回转轴轴心上[9],受人工装配影响较大,增加了测量准备的时间。因此本文提出一种基于激光扫描臂的中子谱仪样品台回转轴几何误差辨识方案,可有效的避免回转轴中心定位问题,保证精度的同时能快速辨识出回转轴各项误差,并通过实验验证了误差辨识模型的准确性。
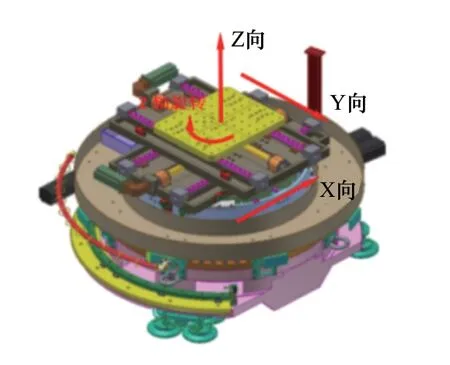
图1 中子谱仪样品台
1 回转轴误差辨识模型
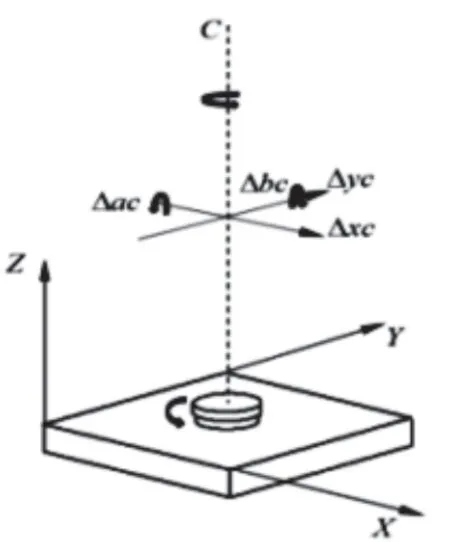
图2 四项位置误差
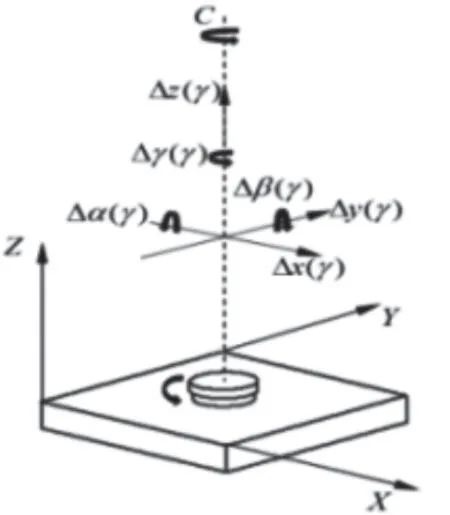
图3 六项运动误差
根据回转轴的运动误差特征可将沿回转轴轴向的误差称为定位误差、绕回转轴的误差称为滚转误差,沿其他两轴的误差称为定位误差绕其他两轴的误差称为颠转误差和偏转误差
1.1 样品台回转轴基准坐标系内各点的总误差辨识模型
在中子谱仪样品台初始位置基准坐标系的X轴线上安装一个高度为h的标准球,以构造探测点。设回转轴的初始坐标系{M}与中子谱仪样品台基准坐标系{S}重合,坐标系原点在样品台回转中心,{S}为定坐标系,{M}为固连在中子谱仪样品台上的动坐标系,ci(i=l,…,n,)为中子谱仪样品台回转轴的角位移。c1=0为初始零位,并以一定角度进行旋转,利用激光扫描臂(如图6所示)探测每个角度位置上的标准球球面坐标(如图4所示),并用最小二乘法拟合得到标准球的球心坐标Pi。设初始零位的标准球球心坐标为标准值,坐标系{M}到坐标系{S}的理想变换矩阵为T(ci),由多体系统理论[18]和坐标的齐次变换原理可计算得到球心Pi经过的理论坐标点为P'i。
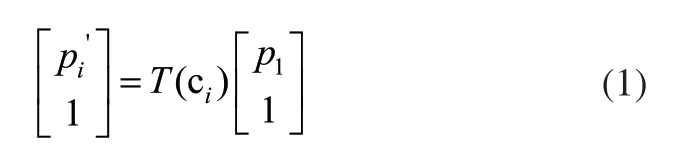
式中:

由于回转轴存在误差,经过旋转后的实际球心坐标为Pi与理论球心坐标P'i两者并不重合,并且存在偏差量Pei。偏差量Pei为中子谱仪样品台回转轴的各项误差的综合表现[2]。

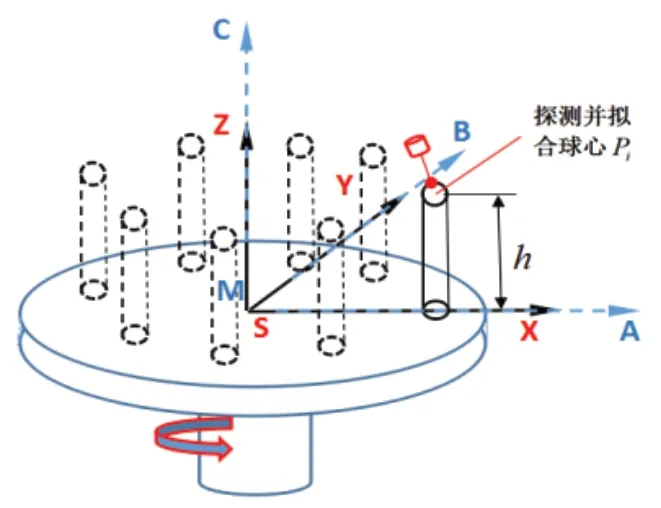
图4 激光扫描臂探测
1.2 四项位置误差辨识模型
回转轴四项位置误差是与回转角度无关的常数项[19],因此对其进行先辨识。首先计算出标准球旋转一周测得的实际球心坐标与理论球心坐标的偏差量,并且认为是由4项位置误差引起的,由于回转轴的四项位置误差值都很小,根据小角度理论,可得:
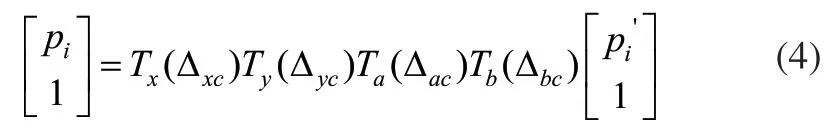
式中:

则位置误差辨识模型为:
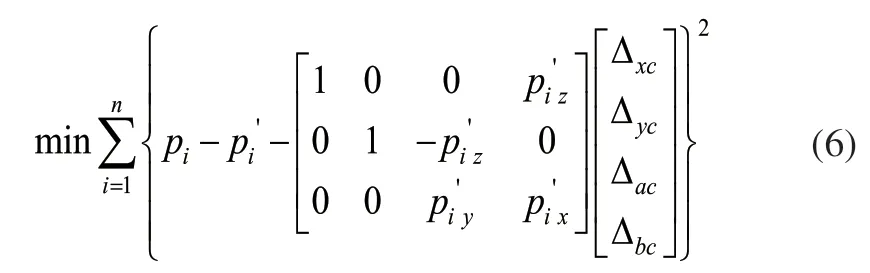
根据上式,采用最小二乘法即可辨识出回转轴的4项位置误差。
1.3 六项运动误差辨识模型
由式(3)可知偏差量Pei为中子谱仪样品台回转轴的各项误差的综合表现,六项运动误差量Plei为Pei去除四项位置误差后的误差项,计算如式(7)所示:
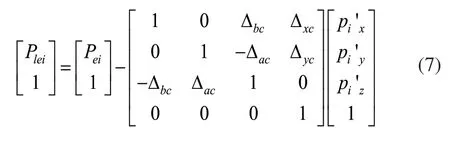
中子谱仪样品台回转轴绕Z轴转动,那么沿Z向的轴向跳动误差一般地与Z轴定位误差,Z轴的颠转误差和Z轴的偏转误差有关,如果测量回转轴中心位置的轴向跳动误差,则Z轴的定位误差就等于此时测量的轴向的跳动误差值,所以Z轴的定位误差可以直接测量回转轴中心位置的轴向跳动误差来直接得出,传统的回转轴误差辨识方案中普遍采用这种方法,但是回转轴中心难以探测且将探测体精确的移动到回转中心比较困难,实验过程也比较复杂,难以得到验证,因此对基于Z轴轴向跳动定位误差辨识模型改进,改进的方案是将被探测的标准球偏置回转轴心一定距离,使其不与回转轴中心重合,直接用Z轴的定位误差,颠转误差,偏转误差进行建模。
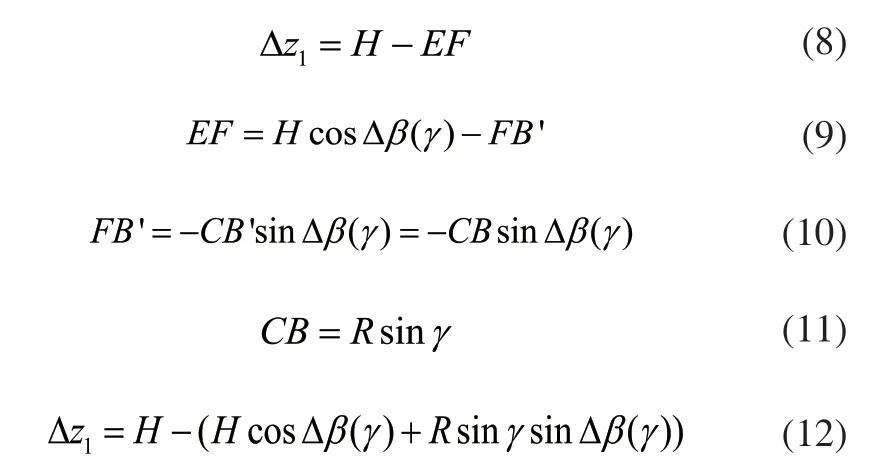
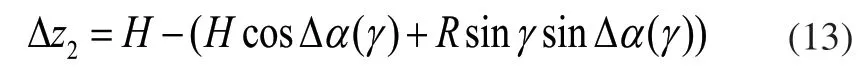
所以:
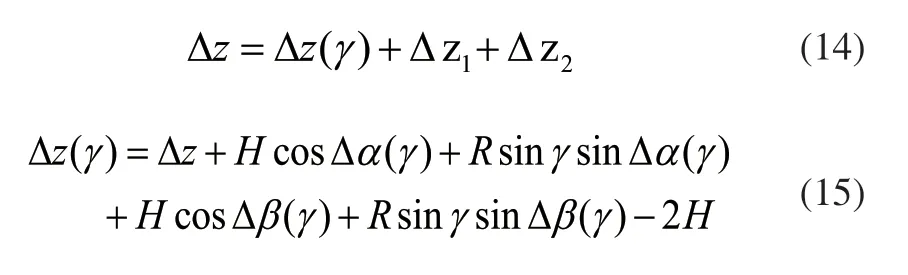

图5 Z轴定位误差辨识

图6 激光扫描臂
六项运动误差辨识模型中的其余各项误差辨识方法主要参见文献[4]。
1.4 回转轴误差预测模型
回转轴误差是由回转轴的预测空间坐标值减去理论空间坐标值得出:
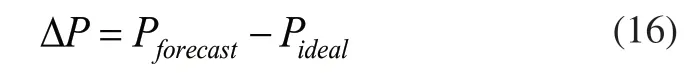
其中:

2 样品台回转轴误差辨识方案
激光扫描臂是由海克斯康测量技术有限公司设计生产,可以测量空间坐标、扫描样品三维模型、逆向等功能,点的重复定位精度为0.027mm。获取标准球球心坐标时用激光扫描臂探测球面五点坐标,探测点布局如图7所示,这五点为三个轴向上的极值点,在回转轴的不同角度下,测头均以固定的方向接触标准球,可减小测头探测误差的影响[2]。

图7 标准球测点布局
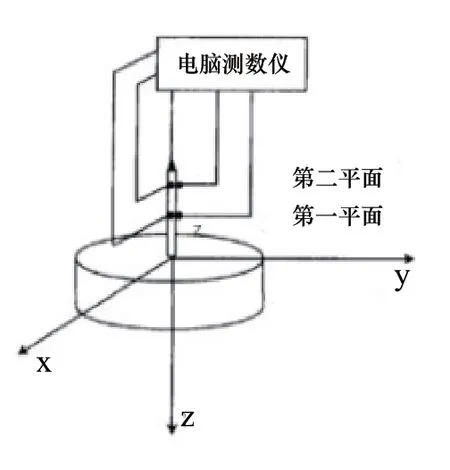
图8 传统的测量方法
传统的回转轴误差辨识方案借助高精度测微仪[4],将标准芯棒安装在回转台中心,径向测量点所在测量平面的间距为100mm,第一平面离转台的最小间距100mm(如图8所示)。由于这种测量方法存在一定的安装误差,标准芯棒不能精确的安装在回转台中心,并且旋转芯棒与中子谱仪样品台平面也不能保证完全垂直,对于实验精度要求高的实验存在一定不合理性。本文提出的新的回转轴误差辨识方案步骤如下:
1)首先用3-2-1法通过激光扫描臂建立中子谱仪样品台在初始位置上的回转轴基准坐标系(如图9所示)。
2)把高精度标准球固定在中子谱仪样品台初始位置X轴上,以经过标准球球心水平面为第一平面,通过激光扫描臂探测并拟合出标准球球心,以10度为单位旋转样品台,探测并拟合出每个位置上标准球球心坐标,将样品台旋转一周得到36个点的球心空间坐标,作为第一组数据。
3)将样品台上升一定距离d(如图10所示)确定经过标准球球心水平面为第二平面,再次重复步骤二得到第二平面上36个标准球球心在基准坐标系中的空间坐标,作为第二组数据,并将坐标值代入式(6)可辨识出四项位置误差。
4)再次将样品台任意升降一定距离,使样品台平面不与第一、二平面重合,重复步骤二得到一组新的标准球球心坐标,作为第三组数据,用于后续实验预测对比。
5)将标准球球心坐标总偏差量扣除四项位置误差便得到回转轴六项运动误差的总误差,将其带入到运动误差模型便可辨识出回转轴的6项运动误差。
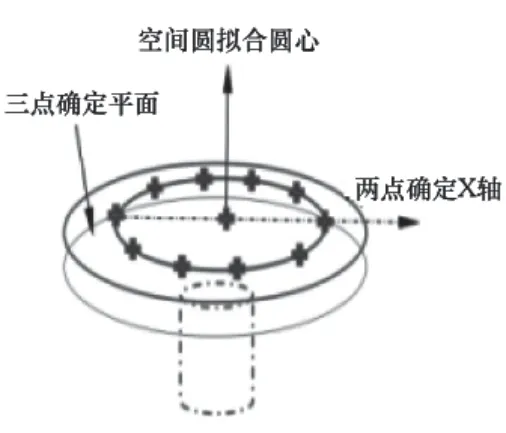
图9 建立基准坐标系

图10 两平面和标准球初始位置
3 实验及结果
在样品台上建立样品台回转轴基准坐标系(如图12所示)。在样品台初始位置X轴上任意位置安装一个由支架支撑的标准球,利用激光扫描臂对标准球进行接触式探测,且以10度为单位旋转样品台,每旋转一次探测一次标准球,每个标准球至少探测五点,旋转一周后得到36个标准球球心坐标。第一平标准球初始坐标位置(71.015,-0.017,178.984)(如图11(a)所示),重复以上步骤三次,计算三组数据的平均值以得到更精确的球心坐标。将样品台上升100mm(如图11(b)所示),得到第二平面位置标准球初始坐标(71.027,-0.028,279.03)。旋转样品台并拟合出第二平面每个角度标准球球心坐标,每个位置同样重复三次求平均值,在polyworks中显示其空间关系(如图13所示)。

图11 两探测平面位置

图12 回转轴基准坐标系

图13 polyworks显示界面
将回转轴第二平面标准球球心坐标值与理论坐标值代入到式(6)中可计算得到四项位置误差:

将总偏差量去除四项位置误差,由式(7)计算可得到六项运动误差引起的偏差,再将计算得到的偏差量带入到运动误差辨识模型,可分别得到六项运动误差在各个角度的误差值,然后通过MATLAB绘制各项误差的二维图并进行曲线拟合,如图14~图19所示。

图14 X轴的定位误差

图15 Y轴的定位误差

图16 Z轴的定位误差

图17 X轴的偏转误差

图18 Y轴的颠转误差

图19 Z轴的滚转误差
通过MATLAB中cftool工具箱对各项误差分别采用8阶多项式拟合、正弦函数拟合,对比两种拟合曲线后发现正弦函数拟合曲线的每个点的逼近程度更高,且确定系数(R-square)更接近1,则拟合效果更好,因此对各项误差数据进行正弦函数拟合,由各项误差拟合公式可建立回转轴误差预测模型,用于预测回转轴任意空间点的误差值。各项误差拟合公式如式(17)~式(22)所示。

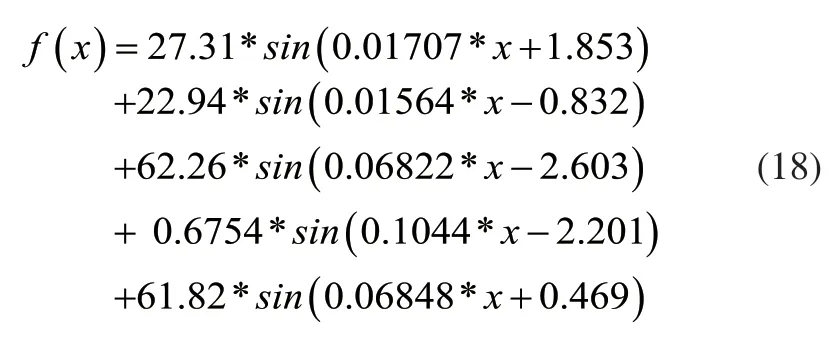




4 模型验与误差预测
通过拟合出的各项误差公式可对样品台基准坐标系内各点坐标进行误差预测,从而得到中子谱仪样品台上任意一点的误差预测值。对实际探测的第三组数据进行预测验证。图20为实际探测误差与预测误差对比,图中纵坐标为总的误差值。
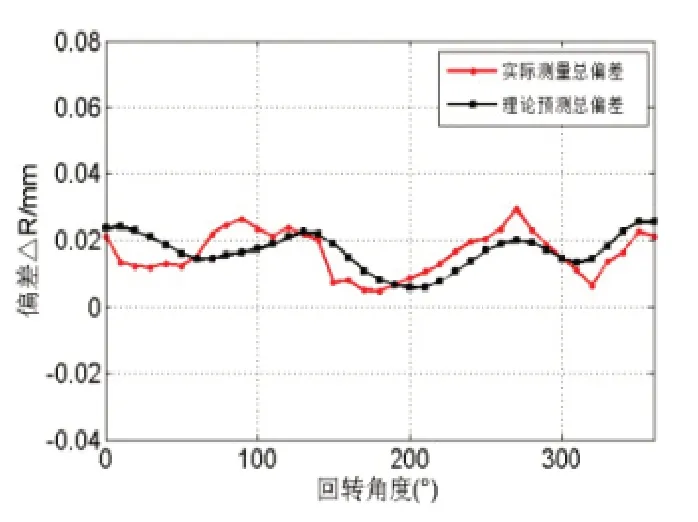
图20 误差预测

图21 残差值
由图20可知预测误差与实际探测误差走势基本一致,图21为预测误差与实际误差的残差,从图中可以看出所有点残差值近80%都在10um以内,可知误差辨识数据准确,误差模型可靠。
5 结论
本文提出了一种中子谱仪样品台回转轴几何误差的辨识方案。运用齐次变换理论,小角度理论和空间几何关系建立样品台回转轴误差辨识模型。标准球可以任意放置于样品台基准坐标系X轴上,避免了传统辨识方案中的标准芯棒与圆心不重合误差和标准芯棒与样品台不垂直的误差,降低了实验难度,能更加快速的辨识出回转轴各项误差。实验方案操作简单,同时测量精度较高,通过实验能准确辨识出各项误差,采用正弦函数拟合出各项误差与运动角度的关系,从而可以对样品台基准坐标系内任意位置的误差进行准确的预测,且预测点80%的残差值在0.01mm内,验证了误差辨识模型的准确性,该误差辨识测量方案快速高效,同时为回转轴误差补偿提供所需要的误差数据。

