格点图上的数学问题设计与课后反思
毛 健,孙琪斌,郑 瑄
(同济大学附属实验中学;上海市嘉定区教育学院;浙江省宁波市江北区教研室)
一、教学素材的来源
题目图1是由4×4个大小完全一样的小正方形组成的方格纸,其中有两个小正方形已经被涂成阴影.试在图1中再选择三个小正方形并涂成阴影,使得图中的五个小正方形组成的阴影部分分别成为:(1)轴对称图形;(2)中心对称图形.

图1
二、阅卷期间的思考
上述题目选自上海市嘉定区七年级第一学期期末教学质量检测第24题.制定评分标准时,关于轴对称图形,命题者罗列了很多方法,学生在试卷上的答案也是多种多样.究竟有多少种方法?如何不重不漏、有序找出符合题意的所有答案?如何引导课堂从“以知识掌握为核心”走进“以思维交流为核心”的境界?如何让学困生与优等生都能够在课堂上获得不同程度的发展?
带着这些问题,上海市同济大学附属实验中学毛健老师以“格点图上的对称问题”为题执教了一节试卷讲评课(区级公开课).在此基础上,孙琪斌老师将该节课进行了教学再设计,并在中国教育学会中学数学教学专业委员会举办的首届“中学数学名师工作室工作研讨与培训会”上作为研究课进行了学术交流.
三、教学设计
1.教学目标及教学重、难点
教学目标:(1)借助格点图直观设计轴对称图形;(2)经历从一个方法到一类方法的探究过程;(3)感受理性思考的需要与必要.
教学重点:在格点图上设计轴对称图形的算法与算理.
教学难点:在格点图上自主设计新问题.
2.活动设置
为了便于交流,使用字母对格点图中的小正方形进行如图2所示的编码.

图2
活动1:小组探究.
(1)找到一个方法;(2)寻找某种规律;(3)提炼通性、通法;(4)思维可视化(清晰、简明地表述思考过程).
学生以小组为单位尝试完成活动1.
活动2:抽签提问.
问题1:你是先想到了符合题意的图形,再尝试寻找其对称轴的,还是先寻找对称轴,再尝试发现符合题意的图形?
活动2是利用抽签的方式随机选择一个小组,展示小组合作学习成果.
追问:以图3中的直线l为对称轴,可以有序地说出符合题意的所有图形吗?可以用最简洁的语言表达这个思考过程吗?

图3
预设思维分解过程如图4所示(思维可视化表达).
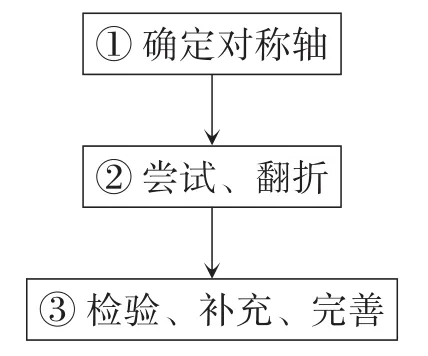
图4
在尝试翻折的过程中,拟以图3为例,重点突出理性思考的过程,引导学生寻找第3个阴影小正方形与第4个小正方形.第3个小正方形或者在对称轴上,或者不在对称轴上.
(1)如果第3个小正方形在对称轴(图3中的直线l)上,那么其关于直线l的对称图形就是它自己.为此,需要寻找第4个小正方形.第4个小正方形如果在直线l上,需要继续寻找第5个小正方形.因为每行每列都只有4个方格,所以第5个小正方形不可能与前四个正方形出现在同一列,一旦第5个小正方形出现在直线l之外,那么必定存在与其对称的第6个小正方形(不符合题意,舍去);由此,第4个小正方形只能出现在直线l之外.
(2)如果第3个小正方形在对称轴(直线l)外,那么必定存在第4个小正方形与之对称.第5个小正方形必定出现在对称轴上.
是否每名学生都能够理性寻找符合题意的图形呢?如何组织已经学会的学生主动帮助暂时尚未学会的学生?如何让每名学困生都能够得到真实有效的帮助,为此拟利用随机抽签确定小组发言人的方式组织第二次教学.
活动3:组织学生在小组内互教互学;利用随机抽签的方式检测合作学习的效果.
问题2:如果再指定一条直线作为对称轴,小组内的每名学生是不是都可以有序地找出符合题意的所有答案?
依据教学情况,随机选择一种情况(如图5),与学生一起交流,促进更多学生达成教学目标.

图5
活动4:应用拓展.
问题3:在解决问题2时,为寻找符合题意的所有图形,你们还可以有序地理性呈现各自的思考过程吗?试设计能够解决问题的具体策略并进行可视化表达.
预设思维分解过程如图6所示(思维可视化表达).

图6
活动5:自主命题,求变创新.
问题4:以如图1所示的4×4个大小完全一样的小正方形组成的方格纸为背景,提出一个新的数学问题.
分组展示各个小组设计的数学问题.
活动6:当堂检测.
问题5:如图7,要求只移动其中的一个阴影小正方形,只移动一次,且每次只移动一个方格(可以前后左右移动,也可以沿正方形的对角线的方向移动),使得移动后的阴影小正方形所组成的图形依然是一个轴对称图形.

图7
四、教学反思
1.忘记基于教学预设的展示,顺应学情,在学中教,因势利导
面对一个具体真实的学习内容,学生的思维水平、思维速度和思维能力均存在客观差异,因此学生不可能以相同的速度、用相同的学习方式同时达成教学目标.因此在教学过程中,在无法规避差异的前提下,教师要充分发挥率先学会的学生身上的资源,将生生之间的差异视为第二次教学的有效资源.教师通过设计问题链,组织学生小组合作探究,将每一个学生当堂达标视为教学目标,引导学生经历真实的学习过程.
在第一次教学(探究问题)的过程中,首先,让学生自主阅读,解决问题,按照例题回答出一种答案;其次,让学生以小组为单位进行交流,搭建“低起点,高水平”的问题链,引导学生将问题层层剥离,尝试从找到一个方法到发现某种规律,再到找到一类方法.在组内合作的过程中,形成思维碰撞,引导学生清晰、简明地表述方法和结果;最后,选择一个小组进行交流分享,其他小组进行补充,深化思维过程,引导学生找到问题的突破口——对称轴.
将小组互助互学、抽签展示、深度追问作为提升二次教学效果的教学改进策略,在学中教,异步达标.在基于教学目标样题的达标检测环节,东莞市东华初级中学九年级301班的学生给出了超出教学预设之外的精彩方法.
对于问题5,学生给出的部分答案如下:将图7中的字母N所在的小正方形移动到字母K所在的位置,即得到符合题意的图形(预设之中的答案).将图7中的字母D所在的小正方形移动到字母H所在的位置,得到符合题意的图形(预设之中的答案).将字母D所在的小正方形移动到格点图的外面,也可以得到符合题意的图形(预设之外的答案).将字母D所在的小正方形移动到字母G所在的位置,均可以得到符合题意的图形(预设之外的答案).
学生将其中的一个小阴影正方形移动到与图中现有的小正方形重合,可以视为“只移动一次,只移动一个方格”,即视为符合题意;从另外一个层面,也可以视为删除了其中的一个小正方形.由于题目要求“只移动其中的一个阴影小正方形,只移动一次,且每次只移动一个方格”,没有限制移动的阴影图形一定要有五个小阴影正方形,所以,学生当堂给出的方法,其实也是抓住了题目设计的漏洞,或者说巧妙利用这个漏洞.从这个意义上说,学生给出的解答,其实就是一种创新,也就是方法的创新、思维方式的创新.
2.从“以知识掌握为核心”走进“以思维分享为核心”,着重引导学生经历理性思考的过程
在教学过程中,我们借助如图8~图10所示的思维导图,重点引导学生经历理性思考的过程.

图8

图9

图10
教师通过提出问题“你是怎样思考的?”实事求是地呈现学生的思考过程,通过问题“为什么这样思考?”引导学生理性分析算法背后的算理,通过问题“还有其他的方法吗?”引导学生求变创新,求美求简(如图11).

图11
该节课较好地呈现了章建跃博士提倡的“数学课堂的终极目标是培养学生的数学核心素养,而数学核心素养的灵魂在于培养学生的逻辑思维,提高推理能力”“课堂教学应当立足于发挥数学的内在力量,发展学生的数学思维能力,培养学生的理性精神”等教学主张.
五、点评
本节课的课堂让人耳目一新,深感震撼!
执教教师是激情万丈的热能源头.执教教师以真诚而独特的人格魅力、鼓励的表情语言、充满教育智慧的扶持与敦促引领着学生一起走进数学的殿堂.本节课中,学生经历从找一个、找一类、最终找到所有的数学活动过程;经历从感性(直觉)走向理性(逻辑)的数学探究过程;经历发现问题、提出问题、分析问题、解决问题,并且不断往复升华的数学研究过程.起初还比较腼腆和拘谨的学生,在执教教师营建的磁场中,脑洞大开,积极主动地各抒己见.执教教师把整个课堂全然交给学生,使得这节探究活动课的氛围达到了高潮.在短短的几十分钟内,执教教师多次令学生爆发出畅然的笑声、自发的掌声,更有台下数百名听课教师由衷热烈的赞美声.一切始于自然,一切始于忘我,一切始于对数学问题的追求、沉醉与痴迷.
执教教师是循循善诱的心灵捕手.课堂中素昧平生的师生,不同寻常的教学素材,无论于教师、于学生都具有一定的挑战性.上课伊始,课堂显得平静又有些许疏离.此时执教教师开始发问:你是怎样想的?你会怎么做?事实上,在课堂上,经常能听见执教教师这样的发问.执教教师引导学生从“发现一个方法”,到思考“发现一类方法”,再理性获得“确定对称轴、翻折、审题检验”的可视化思维路径.他给予学生充足的时间进行独立思考,继而小组讨论,而后小组汇报.同时,又提出新的要求:你们是怎样思考的?为什么这么思考?并让学生给出解题思维的理性简洁的表述.对于学生的表述,执教教师继续不断地追问:你是怎么发现的?你是怎么找到第3个小正方形的位置的?其他小组还有补充吗?六个小组代表均上台发言后,执教教师还要再追问:还有没有其他方法?直到感性散漫的找寻,抵达理性有序的探求.
执教教师是立德树人的榜样楷模.求真、专注、执着、自省、合作、互助……,这些都是教师在课堂中非常关注而崇尚的.当他发现学生的学与他的教并不同步时,当他发现学生学的结果与教学目标不那么一致时,他会退到一个适当的位置,不断地调整反省.在教学中,执教教师认为应该给学生提供学的平台,让他们在学习中暴露自己的问题,教师应该针对学生的问题和困难,进行有针对性地引导,让学生在坚持中,从失败走向成功.同时,执教教师十分注重团队协同合作的力量.显然,在探索、研究的过程中,一些学生会先行理解数学的真谛,执教教师就会让他们去带动那些还不甚理解的学生.每一次团队的共同讨论、互动交流、陈述表达,都是理性、人性、友情、亲情的融融相合.
这样的磁场,谁能舍得离开?
愿所有的教师,都能营建一如执教教师般的磁场,让学生内心的火种能够被点燃,热情激昂,生生不息.

