基于改进GM(1,N)模型的对空情报雷达费用预测

张长聪,方其庆,刘庆华,夏 亮,施端阳

(1.空军预警学院, 武汉 430019；2.73127部队，福州 350500)

随着雷达装备的日趋复杂、装备造价逐步增加，加强装备费用管理工作的科学性、研制计划的综合性以及经济效益的全面性，进一步做好装备费用计划管理工作，合理使用军费和增强装备作战效能显得尤为必要。灰色预测作为灰色系统理论的主要应用之一，因其原理简单、计算简便以及所需数据信息量少等优点，适用于具有小样本、贫信息等特点的对空情报雷达装备费用预测。文献[1]虽然将灰色GM(1,1)模型运用到武器系统费用预测中，并对预测模型进行了改进，提高了预测精度，但该模型只能反映武器装备费用自身的变化规律，无法综合反映外部因素对装备费用的影响，显然其预测结果无法令人信服。文献[2-3]基于灰色关联度分析，分别提出多因素灰色模型和多变量灰色模型，虽综合考虑了多种因素的影响，但未涉及数据的光滑性处理和背景值的优化，其预测精度难以满足要求。因此有必要综合考虑费用的影响因素，建立多因素灰色预测模型。

本文重点针对GM(1,N)模型存在误差较大的问题，以对空情报雷达购置费为研究对象，提出了一种基于改进GM(1,N)模型的费用预测方法。首先利用灰色关联度分析法选择影响装备费用的显著因素并对原始数据进行光滑性处理；其次在研究GM(1,N)模型的背景值的基础上对其进行优化，建立GM(1,N)的改进模型；最后对部分现役对空情报雷达装备购置费进行预测分析和模型对比。

1 GM(1,N)模型

灰色理论最早是由邓聚龙教授于1982年提出，随后在各个领域得到了广泛的应用。灰色GM(1,N)模型是灰色系统理论的主要内容之一，是由多变量构成的一阶微分方程，主要是在“小子样、贫信息”情况下，对某些复杂系统中主导因素与多个相关变量的拟合与预测，揭示主导因素存在的变化规律，从而预测未来的发展变化态势[4-5]。

GM(1,N)模型预测步骤如下：

步骤1进行累加生成运算。

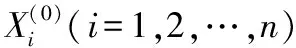
对原始数列进行一次累加生成n个数列，即：

步骤2生成紧邻均值序列。

其中：

(1)

则GM(1,N)模型为：

(2)

对应白化方程为：

(3)

步骤3建立近似时间响应。

(4)

(5)

式(4)、式(5)中：

可得其GM(1,N)模型的近似时间响应为：

(6)

步骤4进行累减还原运算和误差分析。

(7)

设ε(0)={ε(0)(1),ε(0)(2),…,ε(0)(m)}为残差序列，则有：

残差：

(8)

相对误差：

e(k)=|ε(0)(k)|/x(0)(k)×100%

(9)

平均相对误差：

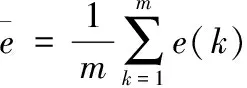
(10)

2 GM(1,N)模型的改进

2.1 灰色关联度分析

采用GM(1,N)模型进行费用预测时，需明确费用与各个因素之间的相互关系。模型显著因素的选择将直接影响到最后的预测精度。预测模型显著因素选择过少，无法有效地反映外部因素对装备费用的影响；显著因素选择过多，则会造成预测结果灰度过大[6-7]。因此对原始数据进行灰色关联度分析，能够有效提高模型的预测精度。

设收集的原始数据矩阵为S(0),则有：

母序列：

子序列：

将原始数据进行无量纲化处理，则有：

式中：k=1,2,…,m。

(11)

(12)

如果γj≥0.5，则可认为母序列与相应子序列有关联。

2.2 数据光滑性处理

考虑到雷达装备采购费用受国民经济、科技发展水平、采购制度等因素影响，采集的原始数据必然存在一定的波动性，而GM(1,N)模型在处理具有波动性的数据序列时存在一定的局限性，原因在于原始数据不能满足预测模型对光滑性的要求。因此为了更准确地预测对空情报雷达装备费用，首先对筛选后的原始数据进行预处理，使处理后的数据满足预测模型对光滑性的要求[9]。

设Q(0)为S(0)经过灰色关联度分析筛选后的原始数据矩阵，X(0)为Q(0)经过对数处理后的建模数据矩阵，记为

其中，

式中,j=1,2,…,n。

为提高原始数据的光滑性，下面对初始数据参数作对数处理，即：

(13)

式(13)中，j=1,2,…,n，k=1,2,…,m。

将处理得到的数据作为模型预测的原始建模数据，预测完成后再对预测结果进行指数还原，即：

(14)

2.3 模型背景值优化

背景值的构造形式是影响模型预测精度的主要因素之一，对背景值的改进能够有效降低模型预测误差，增强模型适用性[10]。文献[11-12]在研究模型背景值与实际背景值关系的基础上，分别给出了背景值优化公式，有效降低了模型背景值产生的误差，提高预测精度。本文在研究背景值构造的基础上，提出GM(1,N)模型背景值的优化方法，从而提高模型预测精度。

引入加权因子λ对式(1)进行重构，即：

z(1)(k)=λx(1)(k)+(1-λ)x(1)(k-1)，

k=2,3,…,n

(15)

λ称为加权系数(0<λ<1)，式(1)为λ=0.5时的特殊情况。

当原始值与模型预测值之差的平均相对误差达到最小，即：

(16)

此时满足上述条件的λ值计算出来的预测结果误差最小，即为最优解。

2.4 模型改进后的计算步骤

基于上述预测模型改进对策，将改进后的模型应用到费用预测中，计算步骤如下：

步骤1收集雷达装备性能参数指标，计算出费用综合因子；选取与费用相关性较大的n个数据建立初始数据S(0)，并进行灰色关联度分析(ρ取0.3)，通过分析结果选取与费用关联度较大的数据序列作为原始数据序列Q(0)。

步骤2将原始数据Q(0)取对数进行光滑性处理，将处理后的数据作为原始建模数据序列X(0)。

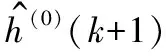
3 实例验证

购置费是对空情报雷达装备全寿命周期费用的重要组成部分，在总费用中占据很大的比重。做好对空情报雷达装备购置费的预测，对加强装备费用管理、科学制定装备采购计划和提高军事经济效益具有重要的实际意义。本文采集了自1986年以来军用对空情报雷达购置费及其相关战技术性能指标，并对数据进行了预处理，提出费用综合因子，采用德尔菲法对与对空情报雷达购置费相关的影响因素进行 4 轮专家意见征询，从中选取了相关性较大的10个参数序列：搜索发现能力、定位能力、抗杂波能力、抗导弹打击能力、抗隐身能力、抗低空突防能力、生存能力、系统可用度、抗有源干扰能力和信息处理能力等[13-14]，记为：Xi(i=2,3,…,11)。

首先，对原始数据进行灰色关联度分析(分辨系数ρ取0.3)，可得到费用与各影响因素之间的关联度γi=(0.83,0.86,0.84,0.75,0.78,0.75,0.75,0.73,0.80,0.82),i=2,3,…,11。预测模型显著因素选取不宜过多也不宜过少，选择过少，无法有效地反映外部因素对费用的影响；选择过多，则会造成预测结果灰度过大。结合本文关联度分析结果，选取关联度大小等于0.8的影响因素：X2、X3、X4、X10和X11，即为搜索发现能力、定位能力、抗杂波能力、抗有源干扰能力和信息处理能力等因素。因此，选取以上5个因素数列作为原始建模数据，建立改进GM(1,6)模型进行费用预测。然后，基于本文提出的改进GM(1,N)模型的计算步骤，通过数据处理和背景值优化，结合Matlab仿真，对我某军在役的6个型号的对空情报雷达装备进行购置费预测，得到了预测结果并进行对比分析。如表1所示，利用本文改进模型对6个型号的对空情报雷达装备在2017—2019年度的购置费用进行了预测，平均相对误差分别为：1.96%、1.94%和1.95%，表明本文方法适用于未来费用预测且精度较高。

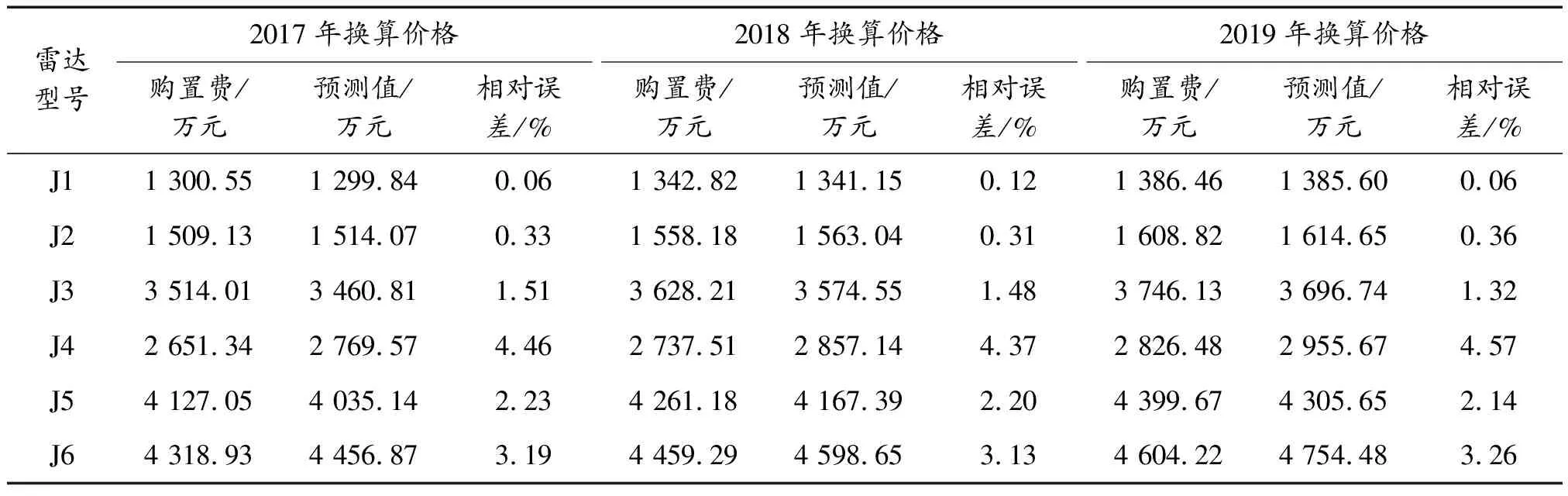
表1 本文模型不同年份预测结果

表2 不同模型预测结果

为了突出本文改进的GM(1,6)模型进行费用预测的优越性，以2019年购置费为例，将预测结果分别与多元线性回归模型、传统GM(1,6)模型进行对比分析，预测结果和相对误差如表2所示。3种模型的平均相对误差分别为7.53%，15.91%，1.95%。从表2的预测结果可以看出，虽然以上3种方法都能够对雷达费用进行预测，但从平均相对误差的大小来看，通过结果分析和比较，在原始数据信息均满足模型预测要求的情况下，本文提出的改进GM(1,6)模型误差最小，传统GM(1,6)模型误差最大。结合表2的预测结果，本文进一步给出了3种方法的实际值与预测值曲线和相对误差曲线，如图1、图2所示。

由图1可以明显看出，对空情报雷达装备购置费波动性较大，呈不稳定性。多元线性回归模型和GM(1,6)模型与实际数据曲线拟合效果较差，相比之下预测精度较低，在预测精度要求较高的情况下并不能很好地满足实际需求。而本文提出的改进模型预测数据与实际数据拟合效果更好，更为接近实际购置费曲线，结果更加符合实际情况，表明了本文方法预测精度更高。

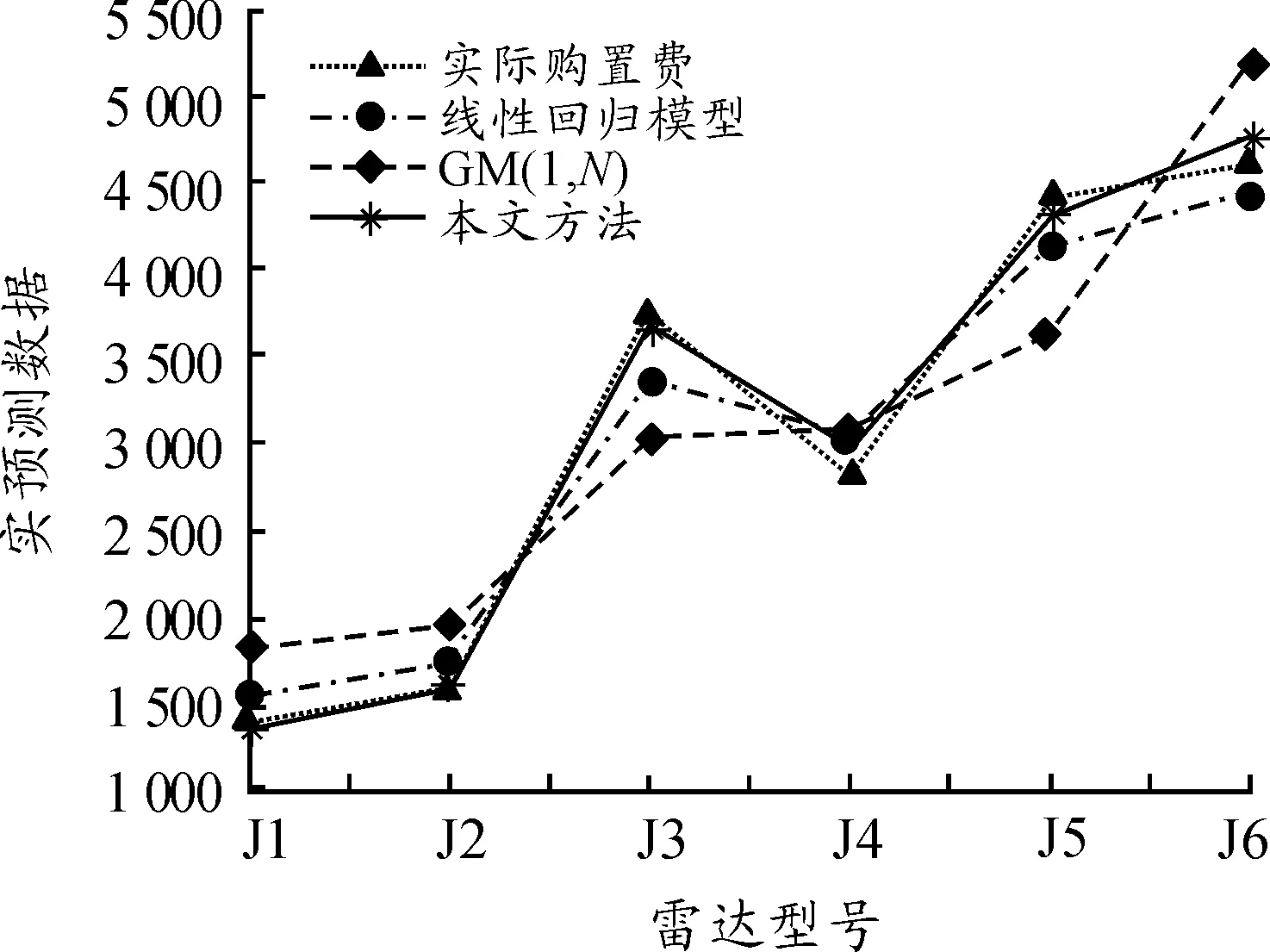
图1 实际值与预测值曲线

从图2对比分析可以得出，以上3种方法中线性回归模型和GM(1,6)模型预测误差较大，其中GM(1,6)模型的误差最大，而相比之下本文提出的预测方法误差最小，说明在小样本、贫信息的情况下，进行费用预测时，本文的改进模型要优于线性回归模型，线性回归模型要优于传统GM(1,N)模型。

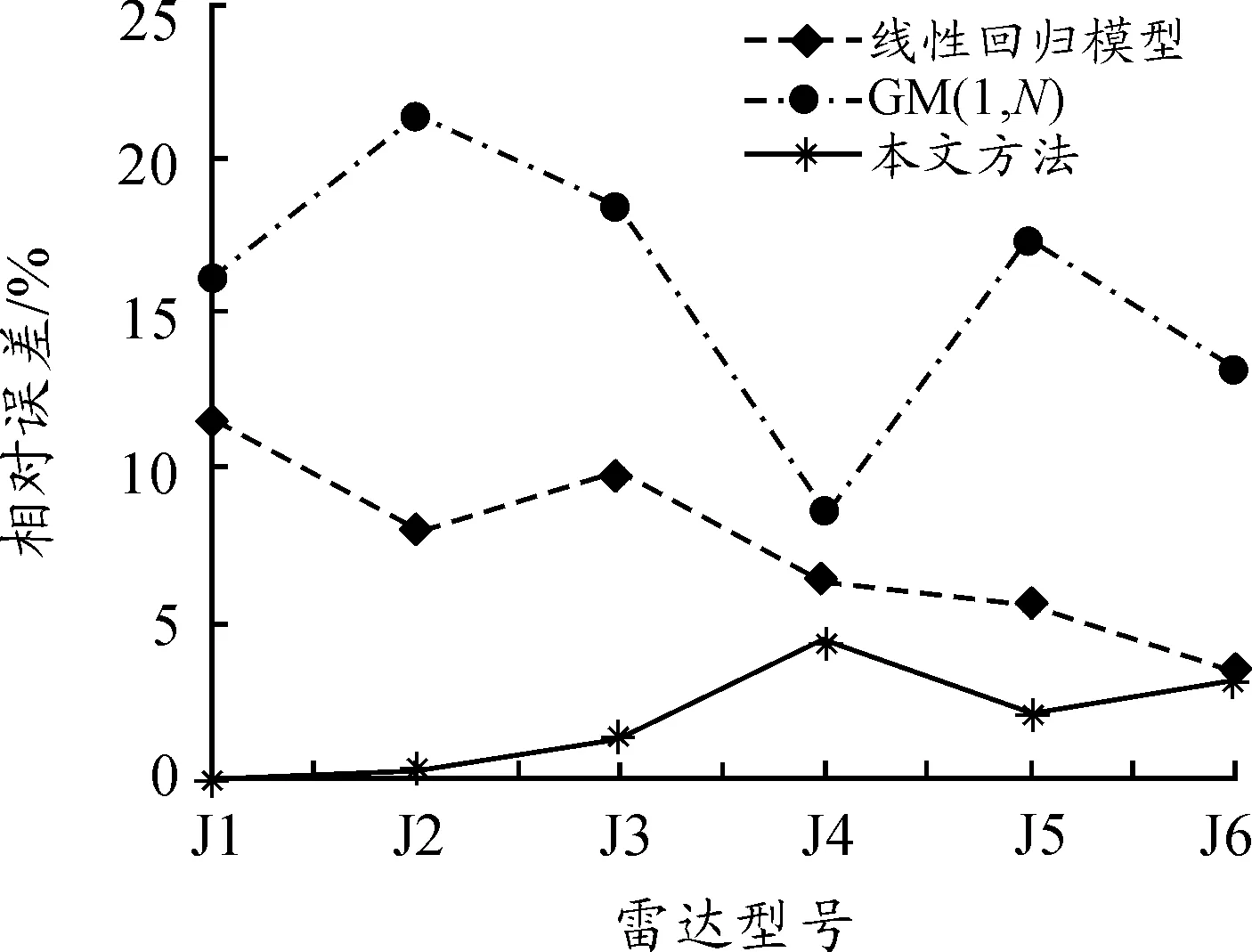
图2 相对误差对比曲线

4 结论

本文提出的改进GM(1,N)模型通过灰色关联度分析、数据光滑性理和背景值优化，提高了模型与实际数据的拟合效果，预测结果更加符合实际情况，充分发挥灰色系统预测所需数据少、预测精度高的优势，且对原始数据的要求不高，无须具有典型的分布规律，相比之下更具有实用性。因此，从对空情报雷达装备费用预测的精度来看，本文提出的改进GM(1,N)模型要明显优于线性回归模型和GM(1,N)模型，在对空情报雷达装备费用预测中具有较强的实用性。